如图,在凸四边形 $ABCD$ 中,$AB$ 与 $CD$ 不平行,圆 $O_1$ 过 $A,B$ 且与边 $CD$ 相切于 $P$,圆 $O_2$ 过 $C,D$ 且与边 $AB$ 相切于 $Q$,圆 $O_1$ 与圆 $O_2$ 相交于 $E,F$.求证:$EF$ 平分线段 $PQ$ 的充分必要条件是 $BC\parallel AD$.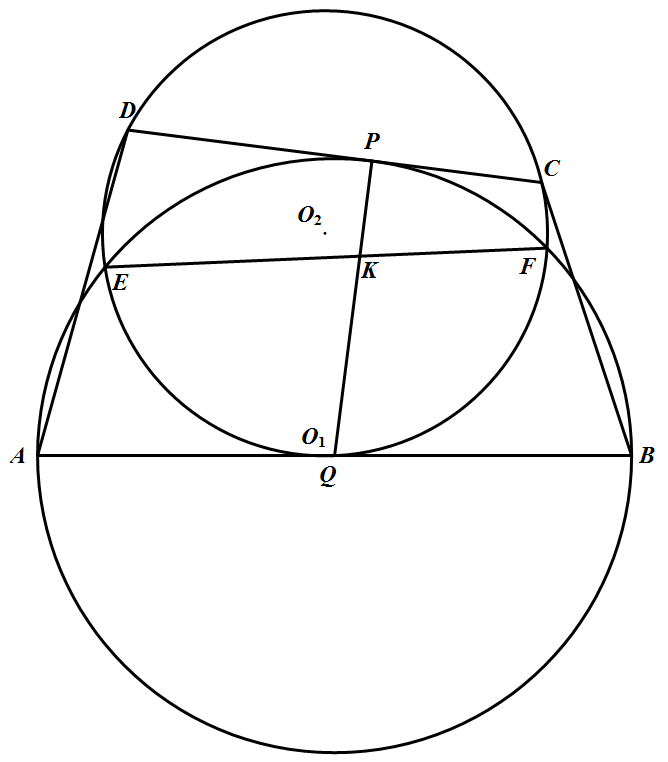

【难度】
【出处】
1990第5届CMO试题
【标注】
【答案】
略
【解析】
延长 $CD$ 与 $BA$ 交于 $I$,又延长 $PQ$,设其交 $O_1$ 与 $H$,交 $O_2$ 于 $G$(图略).先证明 $AD\parallel BC$ 是 $PG=QH$ 的充要条件,这是因为
$P G=Q H \Leftrightarrow D P \cdot P C=A Q \cdot Q B \Leftrightarrow(I P-I D)(I C-I P)=(I Q-I A)(I B-I Q) \Leftrightarrow\\I P \cdot I C-I D \cdot I C-I P^{2}+I D \cdot I P=I Q \cdot I B-I A \cdot I B-I Q^{2}+I A \cdot I Q \Leftrightarrow\\I P(I C+I D)=I Q(I A+I B)^{2} \Leftrightarrow I P^{2}(I C+I D)^{2}=I Q^{2}(I A+I B)^{2} \Leftrightarrow\\I A \cdot I B(I C+I D)^{2}=I C \cdot I D(I A+I B)^{2} \Leftrightarrow(I A \cdot I C-I B \cdot I D)(I B \cdot I C-I A \cdot I D)=0 \Leftrightarrow\\I A \cdot I C=I B \cdot I D(显然I B \cdot I C \neq I A \cdot I D)\Leftrightarrow AD\parallel BC$
所以 $A D / / B C \Leftrightarrow P G=Q H$ 因为 $(G P+P K) K Q=E K \cdot K F=(H Q+Q K) K P$ 所以 $G P \cdot K Q=H Q \cdot K P$ 所以 $P G=Q H \Leftrightarrow K Q=K P$ 这样就得到 $A D / / B C \Leftrightarrow K Q=K P$.
$P G=Q H \Leftrightarrow D P \cdot P C=A Q \cdot Q B \Leftrightarrow(I P-I D)(I C-I P)=(I Q-I A)(I B-I Q) \Leftrightarrow\\I P \cdot I C-I D \cdot I C-I P^{2}+I D \cdot I P=I Q \cdot I B-I A \cdot I B-I Q^{2}+I A \cdot I Q \Leftrightarrow\\I P(I C+I D)=I Q(I A+I B)^{2} \Leftrightarrow I P^{2}(I C+I D)^{2}=I Q^{2}(I A+I B)^{2} \Leftrightarrow\\I A \cdot I B(I C+I D)^{2}=I C \cdot I D(I A+I B)^{2} \Leftrightarrow(I A \cdot I C-I B \cdot I D)(I B \cdot I C-I A \cdot I D)=0 \Leftrightarrow\\I A \cdot I C=I B \cdot I D(显然I B \cdot I C \neq I A \cdot I D)\Leftrightarrow AD\parallel BC$
所以 $A D / / B C \Leftrightarrow P G=Q H$ 因为 $(G P+P K) K Q=E K \cdot K F=(H Q+Q K) K P$ 所以 $G P \cdot K Q=H Q \cdot K P$ 所以 $P G=Q H \Leftrightarrow K Q=K P$ 这样就得到 $A D / / B C \Leftrightarrow K Q=K P$.
答案
解析
备注