凸 $n$ 边形及 $n-3$ 条边在形内不相交的对角线组成的图形称为一个剖分图．求证：当且仅当 $3|n$ 时，存在一剖分图是可以一笔画的圈（即可以从一个顶点出发，经过各线段恰一次，最后回到出发点）．
【难度】
【出处】
1990第5届CMO试题
【标注】
【答案】
略
【解析】
我们先证明所谓的剖分图是 $n$ 边形分成 $n-2$ 个三角形，若不是的话，必然有一些部分是 $m(m>3)$ 边形．容易知道 $n-3$ 条不相交的对角线将 $n$ 边形分为 $n-2$ 块，我们考虑这些剖分的内角和的总和，它大于 $(n-2) \pi$，矛盾。
下面来证明可将这些三角形染红、蓝二色，使有相邻边的三角形染不同颜色，对 $n$ 归纳．$n=3$ 时，显然．设 $n=k$ 时，结论成立．当 $n=k+1$ 时，$n$ 边形被平分成 $k-1$ 个三角形，必有一个三角形的两条边为 $k+1$ 边形的边，去掉这个三角形，剩下的 $k$ 边形由归纳假设可以二染色，再将去掉的三角形染上与它相邻的那个 三角形不同的颜色就可以了．现在可以证明原题了．当此图为一个一笔画的圈时，由欧拉定理，每点发出的边数为偶，于是每顶点发出三角形个数为奇，这就得到 $n$ 边形周界上的三角形都是同种颜色，不妨设为红色．$n$ 边形的每条边，都是一个红三角形的边，它的每条对角线都同时是一个蓝三角形和一个红三角形的边，于是 $3 \times$ 红三角形个数 $-3 \times$ 蓝三角形个数 $=n$ 也就是 $3|n$．当 $n=3l$ 时，我们对 $l$ 进行归纳．$l=1$ 时，结论显然成立．设 $l=k$ 时，结论成立．当 $l=k+1$ 时，如图所示，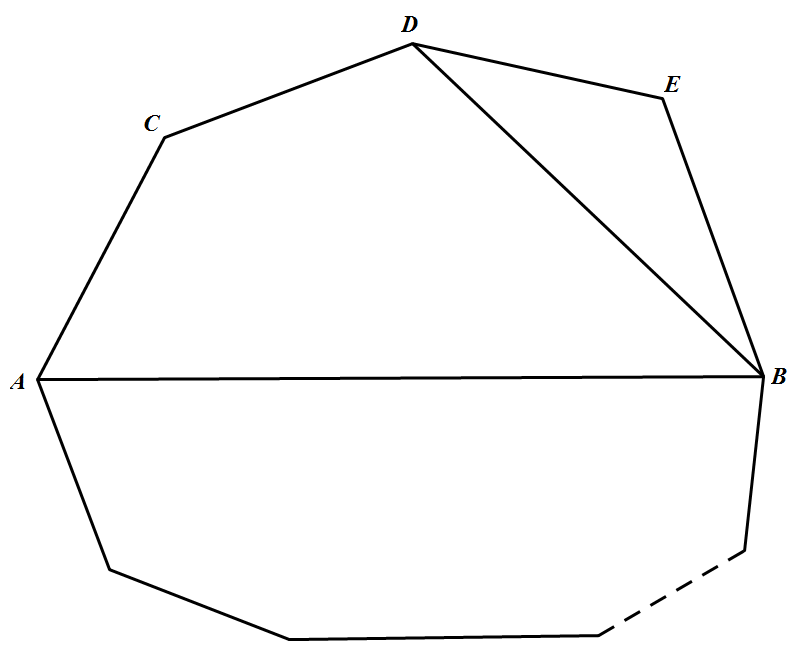
可截出一个五边形，对于 $3k$ 边形，用归纳假设，对五边形，用如图所示的部分，设 $3k$ 边形的一笔画的圈为 $\cdots A B \cdots$，则现在的一笔画的圈为 $\cdots A(B D A C D E) B \cdots$
下面来证明可将这些三角形染红、蓝二色，使有相邻边的三角形染不同颜色，对 $n$ 归纳．$n=3$ 时，显然．设 $n=k$ 时，结论成立．当 $n=k+1$ 时，$n$ 边形被平分成 $k-1$ 个三角形，必有一个三角形的两条边为 $k+1$ 边形的边，去掉这个三角形，剩下的 $k$ 边形由归纳假设可以二染色，再将去掉的三角形染上与它相邻的那个 三角形不同的颜色就可以了．现在可以证明原题了．当此图为一个一笔画的圈时，由欧拉定理，每点发出的边数为偶，于是每顶点发出三角形个数为奇，这就得到 $n$ 边形周界上的三角形都是同种颜色，不妨设为红色．$n$ 边形的每条边，都是一个红三角形的边，它的每条对角线都同时是一个蓝三角形和一个红三角形的边，于是 $3 \times$ 红三角形个数 $-3 \times$ 蓝三角形个数 $=n$ 也就是 $3|n$．当 $n=3l$ 时，我们对 $l$ 进行归纳．$l=1$ 时，结论显然成立．设 $l=k$ 时，结论成立．当 $l=k+1$ 时，如图所示，
可截出一个五边形，对于 $3k$ 边形，用归纳假设，对五边形，用如图所示的部分，设 $3k$ 边形的一笔画的圈为 $\cdots A B \cdots$，则现在的一笔画的圈为 $\cdots A(B D A C D E) B \cdots$
答案
解析
备注
