在平面上画出一个 $9\times 9$ 的方格表，在这些小方格的每一格中都任意填入 $+ 1$ 或 $-1$．下面一种改变填入数字的方式称为作一次变动：对任意一个小方格，凡与此小方格有一条公共边的所有小方格（不包含此格本身）中的数作连乘积，于是每 取一格，就算出一个数．在所有小格都取遍后，再将这些算出的数放人相应的小方格中．试间是否总可以经过有限次变动，使得所有小方格中的数都变为 $1$？
【难度】
【出处】
1992第7届CMO试题
【标注】
【答案】
略
【解析】
容易验证，图中三个数表在上述变动下都是不变的．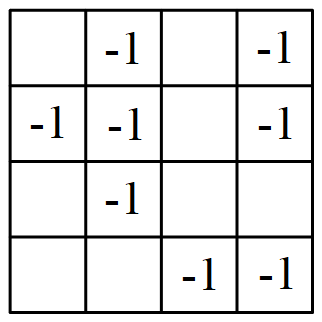
其中没写数的格中都填 $+1$．
将 $9\times 9$ 方格表的中间一行和中间一列的所有方格都填入 $+1$，然后在余下的四个 $4\times 4$ 方格表中对称地填入上面三个数表 中的一个，即得到在规定操作下不变的 $9\times 9$ 数表，如图所示．由此可见，此题的答案是否定的．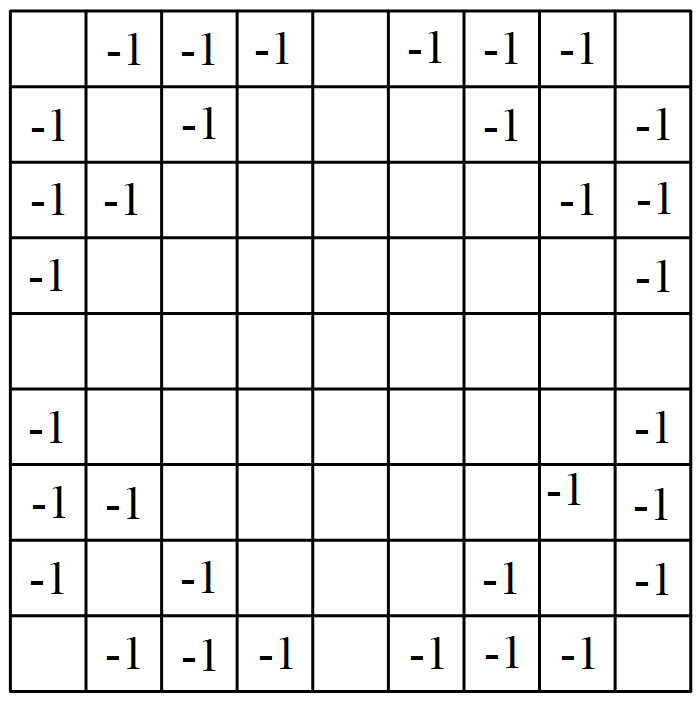
其中没写数的格中都填 $+1$．将 $9\times 9$ 方格表的中间一行和中间一列的所有方格都填入 $+1$，然后在余下的四个 $4\times 4$ 方格表中对称地填入上面三个数表 中的一个，即得到在规定操作下不变的 $9\times 9$ 数表，如图所示．由此可见，此题的答案是否定的．
答案
解析
备注
