设圆 $K$ 和 $K_1$ 同心，它们的半径分别为 $R$ 和 $R_1$，$R_{1}>R$．四边形 $ABCD$ 内接于圆 $K$，四边形 $A_{1} B_{1} C_{1} D_{1}$ 内接于圆 $K_1$，点 $A_{1}, B_{1}, C_{1}, D_{1}$ 分别在射线 $C D, D A, A B, B C$ 上，求证：$\frac{S_{A_{1} B_{1} C_{1} D_{1}}}{S_{A B C D}} \geqslant \frac{R_{1}^{2}}{R^{2}}$
【难度】
【出处】
1993第8届CMO试题
【标注】
【答案】
略
【解析】
如图，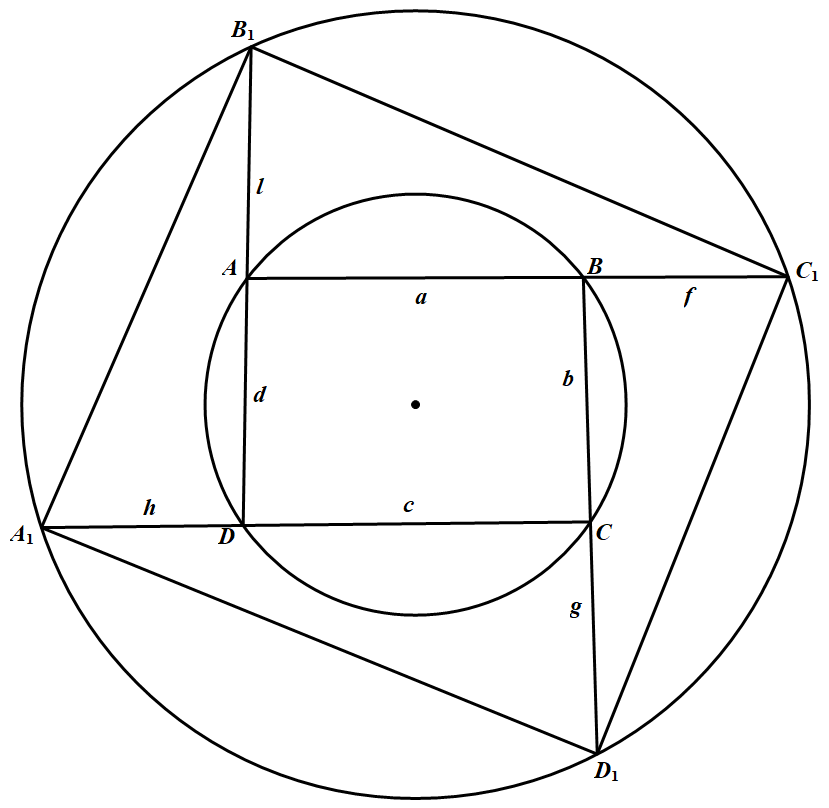
为方便起见，令 $A B=a, B C=b, C D=c,D A=d, A B_{1}=l, B C_{1}=f, C D_{1}=g, D A_{1}=h$，则 $S_{\triangle A B_{1} C_{1}}=\dfrac{1}{2}(a+f) l \sin \angle B_{1} A C_{1}$
$\begin{aligned} S_{A B C D}=& S_{\triangle A B D}+S_{\Delta A B C}= \dfrac{1}{2} a d \sin \angle D A B+\dfrac{1}{2} b c \sin \angle D C B= \dfrac{1}{2}(a d+b c) \sin \angle D A B= \dfrac{1}{2}(a d+b c) \sin \angle B_{1} A C_{1} \end{aligned}$ 故 $\begin{aligned} \dfrac{S_{\Delta A B_{1}} c_{1}}{S_{A B C D}}=\dfrac{(a+f) l}{a d+b c} &=\dfrac{l(l+d)}{a d+b c} \cdot \dfrac{a+f}{l+d}= \dfrac{R_{1}^{2}-R^{2}}{a d+b c} \cdot \dfrac{a+f}{l+d} \end{aligned}$ 同理
$\begin{aligned} \dfrac{S_{\triangle B C_{1} D_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a b+c d} \cdot \dfrac{b+g}{a+f} \\ \dfrac{S_{\triangle C D_{1} A_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a d+b c} \cdot \dfrac{c+h}{b+g} \\ \dfrac{S_{\triangle D A_{1} B_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a b+c d} \cdot \dfrac{l+d}{c+h} \end{aligned}$
将上面四式相加，并应用算术－几何平均值不等式得 $\dfrac{S_{A_1 B_{1} C_{1} D_{1}}-S_{A B C D}}{S_{A B C D}} \geqslant 4\left(R_{1}^{2}-R^{2}\right) \sqrt{\dfrac{1}{(a d+b c)(a b+c d)}}$ 由于 $ABCD$ 内接于半径为 $R$ 的圆，故 $a+b+c+d \leqslant 4 \sqrt{2} R$ 故 $\sqrt{(a d+b c)(a b+c d)} \leqslant \dfrac{a d+b c+a b+c d}{2}=
\dfrac{(a+c)(b+d)}{2} \leqslant\dfrac{1}{2} \dfrac{(a+b+c+d)^{2}}{4} \leqslant 4 R^{2}$ 故 $\dfrac{S_{A_{1} B_{1} C_{1} D_{1}}}{S_{A B C D}} \geqslant 4\left(R_{1}^{2}-R^{2}\right) \dfrac{1}{4 R^{2}}+1=\dfrac{R_{1}^{2}}{R^{2}}$
为方便起见，令 $A B=a, B C=b, C D=c,D A=d, A B_{1}=l, B C_{1}=f, C D_{1}=g, D A_{1}=h$，则 $S_{\triangle A B_{1} C_{1}}=\dfrac{1}{2}(a+f) l \sin \angle B_{1} A C_{1}$$\begin{aligned} S_{A B C D}=& S_{\triangle A B D}+S_{\Delta A B C}= \dfrac{1}{2} a d \sin \angle D A B+\dfrac{1}{2} b c \sin \angle D C B= \dfrac{1}{2}(a d+b c) \sin \angle D A B= \dfrac{1}{2}(a d+b c) \sin \angle B_{1} A C_{1} \end{aligned}$ 故 $\begin{aligned} \dfrac{S_{\Delta A B_{1}} c_{1}}{S_{A B C D}}=\dfrac{(a+f) l}{a d+b c} &=\dfrac{l(l+d)}{a d+b c} \cdot \dfrac{a+f}{l+d}= \dfrac{R_{1}^{2}-R^{2}}{a d+b c} \cdot \dfrac{a+f}{l+d} \end{aligned}$ 同理
$\begin{aligned} \dfrac{S_{\triangle B C_{1} D_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a b+c d} \cdot \dfrac{b+g}{a+f} \\ \dfrac{S_{\triangle C D_{1} A_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a d+b c} \cdot \dfrac{c+h}{b+g} \\ \dfrac{S_{\triangle D A_{1} B_{1}}}{S_{A B C D}} &=\dfrac{R_{1}^{2}-R^{2}}{a b+c d} \cdot \dfrac{l+d}{c+h} \end{aligned}$
将上面四式相加，并应用算术－几何平均值不等式得 $\dfrac{S_{A_1 B_{1} C_{1} D_{1}}-S_{A B C D}}{S_{A B C D}} \geqslant 4\left(R_{1}^{2}-R^{2}\right) \sqrt{\dfrac{1}{(a d+b c)(a b+c d)}}$ 由于 $ABCD$ 内接于半径为 $R$ 的圆，故 $a+b+c+d \leqslant 4 \sqrt{2} R$ 故 $\sqrt{(a d+b c)(a b+c d)} \leqslant \dfrac{a d+b c+a b+c d}{2}=
\dfrac{(a+c)(b+d)}{2} \leqslant\dfrac{1}{2} \dfrac{(a+b+c+d)^{2}}{4} \leqslant 4 R^{2}$ 故 $\dfrac{S_{A_{1} B_{1} C_{1} D_{1}}}{S_{A B C D}} \geqslant 4\left(R_{1}^{2}-R^{2}\right) \dfrac{1}{4 R^{2}}+1=\dfrac{R_{1}^{2}}{R^{2}}$
答案
解析
备注
