在正三棱柱 $ABC-{A_1}{B_1}{C_1}$ 中，若 $AB=\sqrt2B{B_1}$，求证：$A{B_1}\bot$ ${C_1}B$．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
取 $A_1B_1$ 的中点，记为 $M$，连接 $BM$，如图：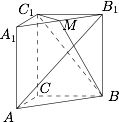
有 $ BM\perp AB_1 $ 且 $ C_1M\perp AB_1 $，于是 $ AB_1\perp BMC_1 $，从而 $ AB_1\perp C_1B$．
有 $ BM\perp AB_1 $ 且 $ C_1M\perp AB_1 $，于是 $ AB_1\perp BMC_1 $，从而 $ AB_1\perp C_1B$．
答案
解析
备注
