空间有四个球，它们的半径分别为 $2,2,3,3$，每个球都与其余 $3$ 个球外切，另有一个小球与那四个球都外切，求该小球的半径．
【难度】
【出处】
1995第10届CMO试题
【标注】
【答案】
略
【解析】
四个球的球心组成四面体 $ABCD$，其中 $A B=A C=3+2=5, A D=3+3=6, B D=C D=3+2=5, B C=2+2=4$．设 $BC,AD$ 的中心分别为 $E,F$，则易知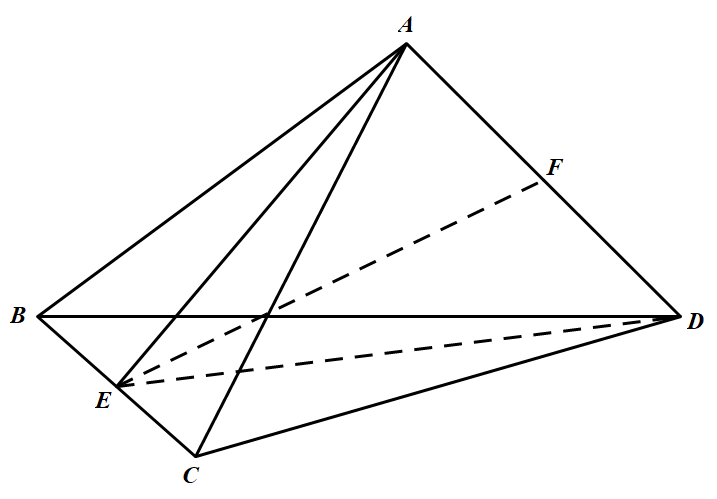
$A E=D E=\sqrt{A C^{2}-C E^{2}}=\sqrt{5^{2}-2^{2}}$
$E F=\sqrt{A E^{2}-A F^{2}}=\sqrt{5^{2}-2^{2}-3^{2}}=\sqrt{12}$
由对称性，小球球心 $O$ 在 $EF$ 上，并且
$\begin{aligned} O E &=\sqrt{O C^{2}-C E^{2}}=\sqrt{(r+2)^{2}-2^{2}} \\ O F &=\sqrt{O A^{2}-A F^{2}}=\sqrt{(r+3)^{2}-3^{2}} \end{aligned}$
（其中 $r$ 为小球半径），从而 $\sqrt{(r+2)^{2}-2^{2}}+\sqrt{(r+3)^{2}-3^{2}}=\sqrt{12}$
即 $\sqrt{r(r+4)}+\sqrt{r(r+6)}=\sqrt{12}$ ①
用 $r(r+6)-r(r+4)=2 r$ 除以上式得 $\sqrt{r}(r+6)-\sqrt{r}(r+4)=\dfrac{r}{\sqrt{3}}$ ②
① + ② 得 $2 \sqrt{r}(r+6)=\sqrt{12}+\dfrac{r}{\sqrt{3}}=\dfrac{6+r}{\sqrt{3}}$ 故 $2 \sqrt{r}=\dfrac{\sqrt{6+} r}{\sqrt{3}}, 4 r=\dfrac{6+r}{3}, r=\dfrac{6}{11}$
求得小球半径为 $\dfrac{6}{11}$．
$A E=D E=\sqrt{A C^{2}-C E^{2}}=\sqrt{5^{2}-2^{2}}$$E F=\sqrt{A E^{2}-A F^{2}}=\sqrt{5^{2}-2^{2}-3^{2}}=\sqrt{12}$
由对称性，小球球心 $O$ 在 $EF$ 上，并且
$\begin{aligned} O E &=\sqrt{O C^{2}-C E^{2}}=\sqrt{(r+2)^{2}-2^{2}} \\ O F &=\sqrt{O A^{2}-A F^{2}}=\sqrt{(r+3)^{2}-3^{2}} \end{aligned}$
（其中 $r$ 为小球半径），从而 $\sqrt{(r+2)^{2}-2^{2}}+\sqrt{(r+3)^{2}-3^{2}}=\sqrt{12}$
即 $\sqrt{r(r+4)}+\sqrt{r(r+6)}=\sqrt{12}$ ①
用 $r(r+6)-r(r+4)=2 r$ 除以上式得 $\sqrt{r}(r+6)-\sqrt{r}(r+4)=\dfrac{r}{\sqrt{3}}$ ②
① + ② 得 $2 \sqrt{r}(r+6)=\sqrt{12}+\dfrac{r}{\sqrt{3}}=\dfrac{6+r}{\sqrt{3}}$ 故 $2 \sqrt{r}=\dfrac{\sqrt{6+} r}{\sqrt{3}}, 4 r=\dfrac{6+r}{3}, r=\dfrac{6}{11}$
求得小球半径为 $\dfrac{6}{11}$．
答案
解析
备注
