设 $H$ 是锐角 $\triangle ABC$ 的垂心，由 $ A$ 向以 $ BC$ 为直径的圆作切线 $AP,AQ$，切点分别为 $ P,Q$．求证：$ P,H,Q$ 三点共线．
【难度】
【出处】
1996第11届CMO试题
【标注】
【答案】
略
【解析】
设 $BC$ 中点为 $O$，联结 $AO,PQ$ 交于点 $G$，于是 $AO\bot PQ$ 设 $AD,BE $ 是 $\triangle ABC$ 的两条高，于是点 $E$ 在圆 $O$ 上，如图所示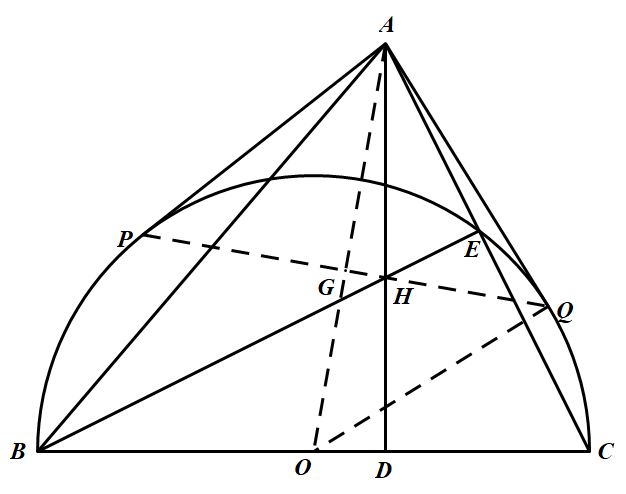
因为 $\angle H E C=90^{\circ}=\angle H D C$，所以 $H, D, C, E$ 四点共圆．所以 $A Q^{2}=A E \cdot A C=A H \cdot A D$ 联结 $OQ$，则 $O Q \perp A Q$．由射影定理有 $A Q^{2}=A G \cdot A D$．所以 $A G \cdot A O=A H \cdot A D$ 所以 $G, O, D, H$ 四点共圆．联结 $HG$．因为 $\angle H D O=90^\circ$，所以 $\angle H G O=90^{\circ}$．所以直线 $HG$ 与 $PQ$ 重合，即 $P,H,Q$ 三点共线．
因为 $\angle H E C=90^{\circ}=\angle H D C$，所以 $H, D, C, E$ 四点共圆．所以 $A Q^{2}=A E \cdot A C=A H \cdot A D$ 联结 $OQ$，则 $O Q \perp A Q$．由射影定理有 $A Q^{2}=A G \cdot A D$．所以 $A G \cdot A O=A H \cdot A D$ 所以 $G, O, D, H$ 四点共圆．联结 $HG$．因为 $\angle H D O=90^\circ$，所以 $\angle H G O=90^{\circ}$．所以直线 $HG$ 与 $PQ$ 重合，即 $P,H,Q$ 三点共线．
答案
解析
备注
