在 $\triangle ABC$ 中，$\angle C=90^{\circ}, \angle A=30^{\circ}, B C=1$．求 $\triangle ABC$ 的内解三角形（三顶点分别在三边上的三角形）的最长边的最小值．
【难度】
【出处】
1996第11届CMO试题
【标注】
【答案】
略
【解析】
首先在 $\triangle ABC$ 的内接正三角形的范围内求边长的最小值．如图，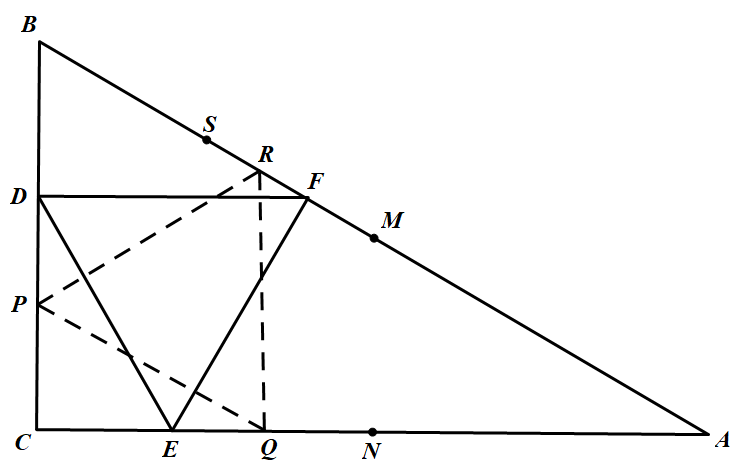
在边 $BC$ 上任取一点 $D$ 并记 $BD= x$，然后分别在边 $CA,AB$ 上取点 $E$ 和 $F$，使 $C E=\dfrac{\sqrt{3}}{2} x, B F=1-\dfrac{x}{2}$．于是由余弦定理有
$D F^{2}=x^{2}+\left(1-\dfrac{x}{2}\right)^{2}-2 x\left(1-\dfrac{x}{2}\right) \cos 60^{\circ}=\dfrac{7}{4} x^{2}-2 x+1$
$D E^{2}=(1-x)^{2}+\left(\dfrac{\sqrt{3}}{2} x\right)^{2}=\dfrac{7}{4} x^{2}-2 x+1$
$E F^{2}=\left(\sqrt{3}-\dfrac{\sqrt{3}}{2} x\right)^{2}+\left(1+\dfrac{x}{2}\right)^{2}-2 \sqrt{3}\left(1-\dfrac{x}{2}\right)\left(1+\dfrac{x}{2}\right) \cos 30^{\circ}=\dfrac{7}{4} x^{2}-2 x+1$
故得 $DF=DE= EF$，即 $\triangle DEF$ 为正三角形这表明对于 $BC$ 上的任何一点 $D$，都可以作出一个内接正三角形．记 $CA,AB$ 中点分别为 $N,M$，记 $BM$ 中点为 $S$，则当点 $D$ 从 $B$ 变到 $C$ 时，点 $E$ 从 $C$ 变到 $N$，点 $F$ 从 $M$ 变到 $S$．若记 $\triangle DEF$ 的边长为 $a$，则有
$\begin{aligned} a^{2}=& \dfrac{7}{4} x^{2}-2 x+1=\dfrac{7}{4}\left(x^{2}-\dfrac{8}{7} x+\dfrac{4}{7}\right) \dfrac{7}{4}\left(\left(x-\dfrac{4}{7}\right)^{2}-\dfrac{16}{49}+\dfrac{4}{7}\right)=\dfrac{7}{4}\left(x-\dfrac{4}{7}\right)^{2}+\dfrac{3}{7} \end{aligned}$
可见，当 $x=\dfrac{4}{7}$ 时，边长 $a$ 取得最小值 $\sqrt{\dfrac{3}{7}}$．图中虚线所示的 $\triangle PQR$ 即为取最小值的位置．
下面证明，任何内接三角形的最大边的边长都不小于 $\sqrt{\dfrac{3}{7}}$．为方便计，引入以 $C$ 为原点，$CA$ 为正半 $x$ 轴的直角坐标系（图如下）．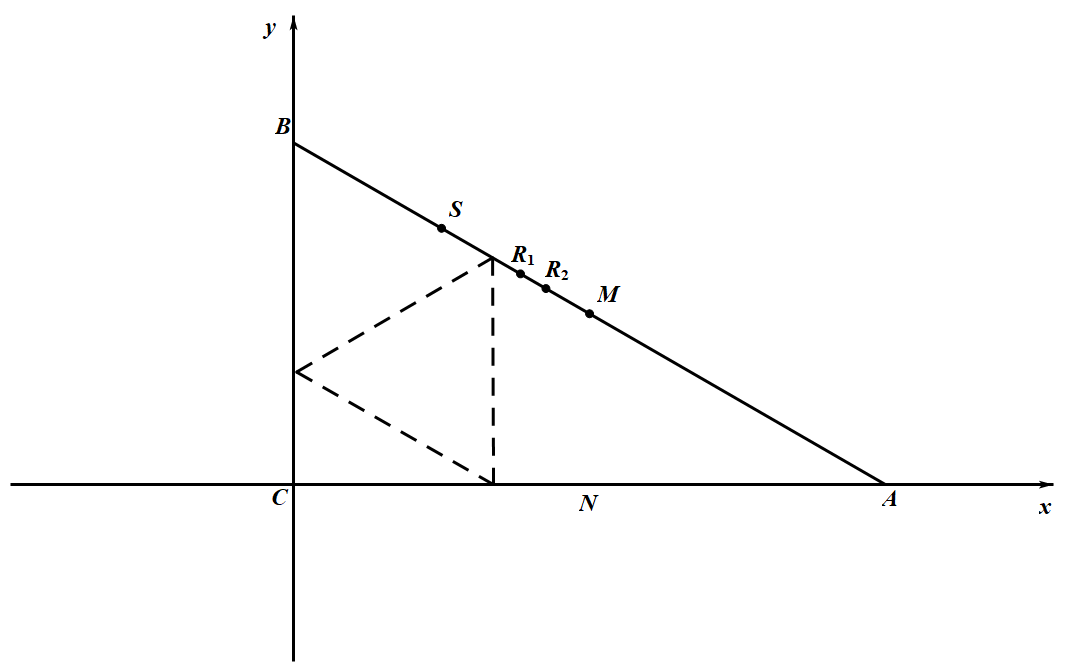
设 $\triangle XYZ$ 为 $\triangle ABC$ 的任一内接三角形，其中点 $X,Y,Z$ 分别位于边 $BC, CA,AB$ 上．在 $BM$ 上取点 $R_1$ 和 $R_2$，使得 $M R_{1}=\dfrac{1}{3} M B,M R_{2}=\dfrac{3}{14} M B$ 于是 $A R_{1}=\dfrac{2}{3} A B, B R_{2}=\dfrac{11}{14} B M$，从而有 $y_{R_{1}}=\dfrac{2}{3}>\sqrt{\dfrac{3}{7}},x_{R_{2}}=\dfrac{11}{14} \times \dfrac{\sqrt{3}}{2}>\dfrac{10}{13} \times \dfrac{\sqrt{3}}{2}>\sqrt{\dfrac{3}{7}}$
（1）若点 $Z$ 位于线段 $BR_1$ 上，则 $y_{z} \geqslant y_{R_{1}}>\sqrt{\dfrac{3}{7}}$；若点 $Z$ 位于线段 $R_2A$ 上，则 $x_{Z} \geqslant x_{R_{2}}>\sqrt{\dfrac{3}{7}}$．可见这时 $\triangle XYZ$ 的最长边的边长大于 $\sqrt{\dfrac{3}{7}}$
（2）设点 $Z$ 位于线段 $R_1R_2$ 内部，则将点 $Z$ 作为点 $F$，作证明开头所述的正 $\triangle DEF$．不难验证，$x_{E}<x_{F}, y_{D}<y_{F}$．因而，若点 $X$ 位于线段 $DC$ 上，则 $Z X \geqslant Z D=F D$；若点 $Y$ 位于线段 $CE$ 上，则 $Z Y \geqslant Z E=F E$；若点 $X$ 位于 $BD$ 上，且点 $Y$ 位于 $EA$ 上，则由勾股定理知 $X Y \geqslant D E$．所以 $\triangle XYZ$ 的最长边的边长不小于 $\triangle DEF$ 的边长，从而不小于 $\sqrt{\dfrac{3}{7}}$．
综上可知，所求的最长边的最小值为 $\sqrt{\dfrac{3}{7}}$．
在边 $BC$ 上任取一点 $D$ 并记 $BD= x$，然后分别在边 $CA,AB$ 上取点 $E$ 和 $F$，使 $C E=\dfrac{\sqrt{3}}{2} x, B F=1-\dfrac{x}{2}$．于是由余弦定理有$D F^{2}=x^{2}+\left(1-\dfrac{x}{2}\right)^{2}-2 x\left(1-\dfrac{x}{2}\right) \cos 60^{\circ}=\dfrac{7}{4} x^{2}-2 x+1$
$D E^{2}=(1-x)^{2}+\left(\dfrac{\sqrt{3}}{2} x\right)^{2}=\dfrac{7}{4} x^{2}-2 x+1$
$E F^{2}=\left(\sqrt{3}-\dfrac{\sqrt{3}}{2} x\right)^{2}+\left(1+\dfrac{x}{2}\right)^{2}-2 \sqrt{3}\left(1-\dfrac{x}{2}\right)\left(1+\dfrac{x}{2}\right) \cos 30^{\circ}=\dfrac{7}{4} x^{2}-2 x+1$
故得 $DF=DE= EF$，即 $\triangle DEF$ 为正三角形这表明对于 $BC$ 上的任何一点 $D$，都可以作出一个内接正三角形．记 $CA,AB$ 中点分别为 $N,M$，记 $BM$ 中点为 $S$，则当点 $D$ 从 $B$ 变到 $C$ 时，点 $E$ 从 $C$ 变到 $N$，点 $F$ 从 $M$ 变到 $S$．若记 $\triangle DEF$ 的边长为 $a$，则有
$\begin{aligned} a^{2}=& \dfrac{7}{4} x^{2}-2 x+1=\dfrac{7}{4}\left(x^{2}-\dfrac{8}{7} x+\dfrac{4}{7}\right) \dfrac{7}{4}\left(\left(x-\dfrac{4}{7}\right)^{2}-\dfrac{16}{49}+\dfrac{4}{7}\right)=\dfrac{7}{4}\left(x-\dfrac{4}{7}\right)^{2}+\dfrac{3}{7} \end{aligned}$
可见，当 $x=\dfrac{4}{7}$ 时，边长 $a$ 取得最小值 $\sqrt{\dfrac{3}{7}}$．图中虚线所示的 $\triangle PQR$ 即为取最小值的位置．
下面证明，任何内接三角形的最大边的边长都不小于 $\sqrt{\dfrac{3}{7}}$．为方便计，引入以 $C$ 为原点，$CA$ 为正半 $x$ 轴的直角坐标系（图如下）．
设 $\triangle XYZ$ 为 $\triangle ABC$ 的任一内接三角形，其中点 $X,Y,Z$ 分别位于边 $BC, CA,AB$ 上．在 $BM$ 上取点 $R_1$ 和 $R_2$，使得 $M R_{1}=\dfrac{1}{3} M B,M R_{2}=\dfrac{3}{14} M B$ 于是 $A R_{1}=\dfrac{2}{3} A B, B R_{2}=\dfrac{11}{14} B M$，从而有 $y_{R_{1}}=\dfrac{2}{3}>\sqrt{\dfrac{3}{7}},x_{R_{2}}=\dfrac{11}{14} \times \dfrac{\sqrt{3}}{2}>\dfrac{10}{13} \times \dfrac{\sqrt{3}}{2}>\sqrt{\dfrac{3}{7}}$（1）若点 $Z$ 位于线段 $BR_1$ 上，则 $y_{z} \geqslant y_{R_{1}}>\sqrt{\dfrac{3}{7}}$；若点 $Z$ 位于线段 $R_2A$ 上，则 $x_{Z} \geqslant x_{R_{2}}>\sqrt{\dfrac{3}{7}}$．可见这时 $\triangle XYZ$ 的最长边的边长大于 $\sqrt{\dfrac{3}{7}}$
（2）设点 $Z$ 位于线段 $R_1R_2$ 内部，则将点 $Z$ 作为点 $F$，作证明开头所述的正 $\triangle DEF$．不难验证，$x_{E}<x_{F}, y_{D}<y_{F}$．因而，若点 $X$ 位于线段 $DC$ 上，则 $Z X \geqslant Z D=F D$；若点 $Y$ 位于线段 $CE$ 上，则 $Z Y \geqslant Z E=F E$；若点 $X$ 位于 $BD$ 上，且点 $Y$ 位于 $EA$ 上，则由勾股定理知 $X Y \geqslant D E$．所以 $\triangle XYZ$ 的最长边的边长不小于 $\triangle DEF$ 的边长，从而不小于 $\sqrt{\dfrac{3}{7}}$．
综上可知，所求的最长边的最小值为 $\sqrt{\dfrac{3}{7}}$．
答案
解析
备注
