四边形 $ABCD$ 内接于圆，其边 $AB$ 与 $DC$ 的延长线交于点 $P$，$AD$ 与 $BC$ 的延长线交于点 $Q$，由 $ Q$ 作该圆的两条切线 $QE$ 和 $QF$，切点分别为 $ E,F$．
求证：$P,E,F$ 三点共线．
求证：$P,E,F$ 三点共线．
【难度】
【出处】
1997第12届CMO试题
【标注】
【答案】
略
【解析】
如图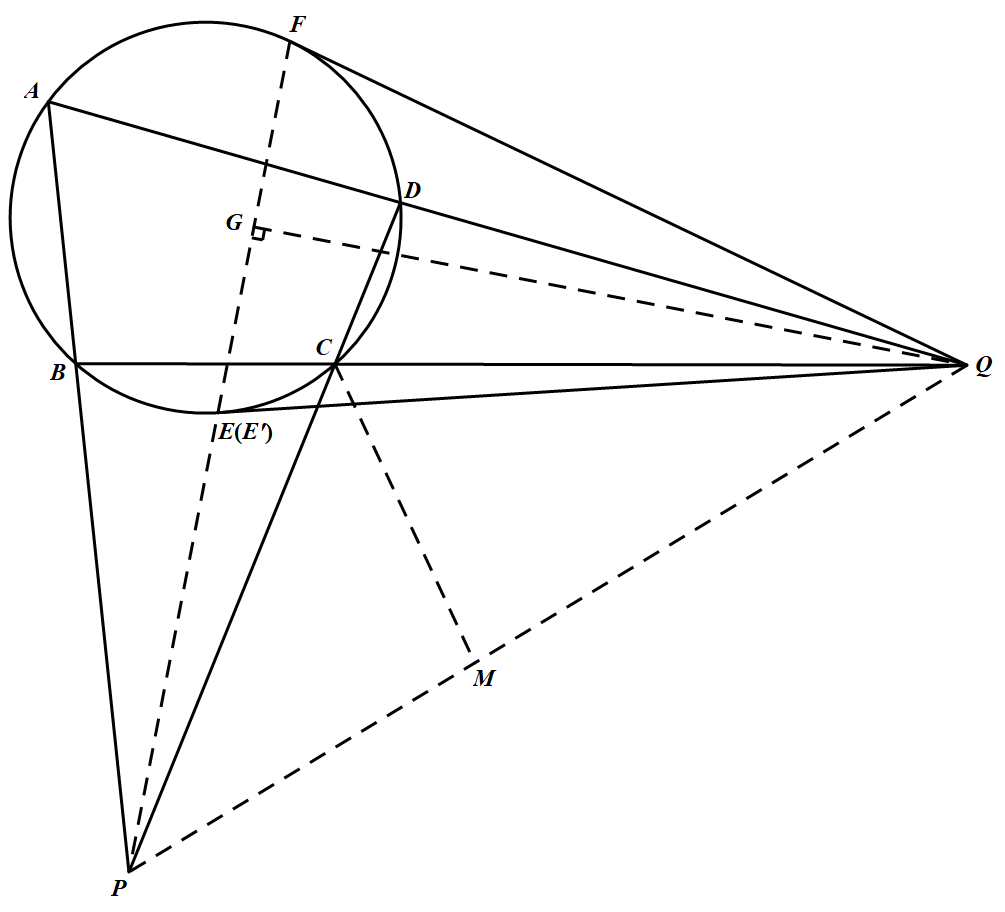
联结 $PQ$，并在 $PQ$ 上取一点 $M$，使得 $B,C,M,P$ 四点共圆，
则 $Q E^{2}=Q M \cdot Q P=Q C \cdot Q B$ ①
以及 $\angle P M C=\angle P D Q$．从而 $C,D,Q,M$ 四点共圆．于是 $P M \cdot P Q=P C \cdot P D$ ②
由 ①，②，有 $P Q^{2}=Q C \cdot Q B+P C \cdot P D$
联结 $PF$，设 $PF $ 与圆的另一交点为 $E$，作 $QC$ 垂直于 $PF$，垂足为 $G$，则 $P D \cdot P C=P E^{\prime} \cdot P F,Q F^{2}=Q C \cdot Q B$ 所以 $P E^{\prime} \cdot P F+Q F^{2}=P Q^{2}$ 即 $P E^{\prime} \cdot P F=P Q^{2}-Q E^{2}$ 又 $\begin{aligned} P Q^{2}-Q F^{2}=& P G^{2}-G F^{2}=(P G-G F)(P G+G F)= P F(P G-G F) \end{aligned}$ 从而 $P G-G F=P E^{\prime}=P G-G E^{\prime}$ 即 $G F=G E^{\prime}$ 故点 $E^\prime $ 与 $E$ 重合．
联结 $PQ$，并在 $PQ$ 上取一点 $M$，使得 $B,C,M,P$ 四点共圆，则 $Q E^{2}=Q M \cdot Q P=Q C \cdot Q B$ ①
以及 $\angle P M C=\angle P D Q$．从而 $C,D,Q,M$ 四点共圆．于是 $P M \cdot P Q=P C \cdot P D$ ②
由 ①，②，有 $P Q^{2}=Q C \cdot Q B+P C \cdot P D$
联结 $PF$，设 $PF $ 与圆的另一交点为 $E$，作 $QC$ 垂直于 $PF$，垂足为 $G$，则 $P D \cdot P C=P E^{\prime} \cdot P F,Q F^{2}=Q C \cdot Q B$ 所以 $P E^{\prime} \cdot P F+Q F^{2}=P Q^{2}$ 即 $P E^{\prime} \cdot P F=P Q^{2}-Q E^{2}$ 又 $\begin{aligned} P Q^{2}-Q F^{2}=& P G^{2}-G F^{2}=(P G-G F)(P G+G F)= P F(P G-G F) \end{aligned}$ 从而 $P G-G F=P E^{\prime}=P G-G E^{\prime}$ 即 $G F=G E^{\prime}$ 故点 $E^\prime $ 与 $E$ 重合．
答案
解析
备注
