设 $D$ 为锐角 $\triangle ABC$ 内部一点，且满足条件：$DA\cdot DB\cdot AB+ DB\cdot DC\cdot BC + DC\cdot DA\cdot CA = AB\cdot BC\cdot CA$．试确定点 $D$ 的几何位置，并证明你的结论．
【难度】
【出处】
1998第13届CMO试题
【标注】
【答案】
略
【解析】
此题我们改证比其更强的命题如下：
设 $D$ 为锐角 $\triangle ABC$ 内部一点．求证：$DA\cdot DB\cdot AB+ DB\cdot DC\cdot BC + DC\cdot DA\cdot CA \geqslant AB\cdot BC\cdot CA$ $(*)$ 并且等号当且仅当 $D$ 为 $\triangle ABC$ 的垂心时才成立．如图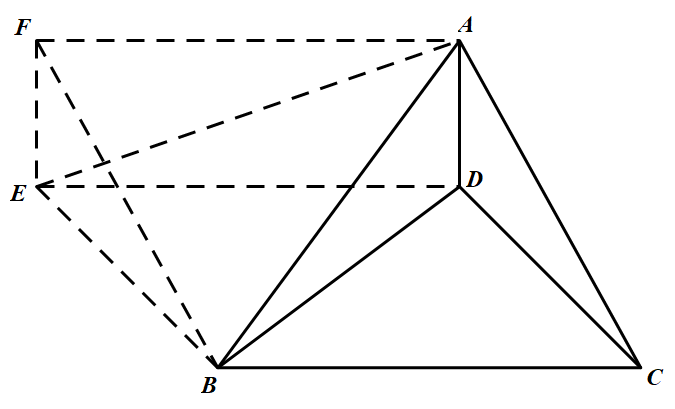
作 $ED\underline{\underline{\parallel }}BC$，$FA \underline{\underline{\parallel }} ED$，则 $BCDE$ 和 $ADEF$ 均是平行四边形．联结 $BF$ 和 $AE$，显然 $BCAF$ 也是平行四边形．于是 $AF= ED = BC,EF = AD, EB = CD, BF = AC $ 在四边形 $ABEF$ 和 $AEBD$ 中，由托勒密不等式得 $AB\cdot EF + AF\cdot BE\geqslant AE\cdot BF,BD \cdot AE + AD\cdot BE \geqslant AB\cdot ED$
即 $AB\cdot AD + BC\cdot CD\geqslant AE\cdot AC$ ①
$BD\cdot AE + AD\cdot CD\geqslant AB\cdot BC$ ②
于是，由 ① 和 ② 可得
$DA\cdot DB\cdot AB + DB\cdot DC\cdot BC + DC\cdot DA\cdot CA = DB(AB\cdot AD + BC\cdot CD)+ DC\cdot DA\cdot CA\\\geqslant DB\cdot AE\cdot AC + DC\cdot DA\cdot AC =AC(DB\cdot AE + DC\cdot AD)=AC\cdot BC\cdot AB$
故式 $(*)$ 得证，且等号成立的充分必要条件是 ① 和 ② 的等号同时都成立，即等号当且仅当 $ABEF$ 及 $AEBD$ 都是圆内接四边形时，亦即 $AFEBD$ 恰是圆内接五边形时等号成立．由于 $AFED$ 为平行四边形，所以条件等价于 $AFED$ 为矩形（即 $AD\bot BC$）且 $\angle ABE=\angle ADE=90^\circ$，亦等价于 $AD\bot BC$ 且 $CD\bot AB$，所以式 $(*)$ 等式成立的充分必要条件是 $D$ 为 $\triangle ABC$ 的垂心．
设 $D$ 为锐角 $\triangle ABC$ 内部一点．求证：$DA\cdot DB\cdot AB+ DB\cdot DC\cdot BC + DC\cdot DA\cdot CA \geqslant AB\cdot BC\cdot CA$ $(*)$ 并且等号当且仅当 $D$ 为 $\triangle ABC$ 的垂心时才成立．如图
作 $ED\underline{\underline{\parallel }}BC$，$FA \underline{\underline{\parallel }} ED$，则 $BCDE$ 和 $ADEF$ 均是平行四边形．联结 $BF$ 和 $AE$，显然 $BCAF$ 也是平行四边形．于是 $AF= ED = BC,EF = AD, EB = CD, BF = AC $ 在四边形 $ABEF$ 和 $AEBD$ 中，由托勒密不等式得 $AB\cdot EF + AF\cdot BE\geqslant AE\cdot BF,BD \cdot AE + AD\cdot BE \geqslant AB\cdot ED$即 $AB\cdot AD + BC\cdot CD\geqslant AE\cdot AC$ ①
$BD\cdot AE + AD\cdot CD\geqslant AB\cdot BC$ ②
于是，由 ① 和 ② 可得
$DA\cdot DB\cdot AB + DB\cdot DC\cdot BC + DC\cdot DA\cdot CA = DB(AB\cdot AD + BC\cdot CD)+ DC\cdot DA\cdot CA\\\geqslant DB\cdot AE\cdot AC + DC\cdot DA\cdot AC =AC(DB\cdot AE + DC\cdot AD)=AC\cdot BC\cdot AB$
故式 $(*)$ 得证，且等号成立的充分必要条件是 ① 和 ② 的等号同时都成立，即等号当且仅当 $ABEF$ 及 $AEBD$ 都是圆内接四边形时，亦即 $AFEBD$ 恰是圆内接五边形时等号成立．由于 $AFED$ 为平行四边形，所以条件等价于 $AFED$ 为矩形（即 $AD\bot BC$）且 $\angle ABE=\angle ADE=90^\circ$，亦等价于 $AD\bot BC$ 且 $CD\bot AB$，所以式 $(*)$ 等式成立的充分必要条件是 $D$ 为 $\triangle ABC$ 的垂心．
答案
解析
备注
