$\triangle ABC$ 的三边长分别为 $a,b,c$，$b< c$，$AD$ 是 $\angle A$ 的内角平分线，点 $D$ 在 $BC$ 上．
（1）求在线段 $AB,AC$ 内分别存在点 $E,F$（不是端点）满足 $BE=CF$ 和 $\angle BDE=\angle GDF$ 的充分必要条件（用 $\angle A,\angle B,\angle C$ 表示）；
（2）在点 $E$ 和 $F$ 存在情况下，用 $a,b,c$ 表示 $BE$ 的长．
（1）求在线段 $AB,AC$ 内分别存在点 $E,F$（不是端点）满足 $BE=CF$ 和 $\angle BDE=\angle GDF$ 的充分必要条件（用 $\angle A,\angle B,\angle C$ 表示）；
（2）在点 $E$ 和 $F$ 存在情况下，用 $a,b,c$ 表示 $BE$ 的长．
【难度】
【出处】
2002第17届CMO试题
【标注】
【答案】
略
【解析】
（1）如图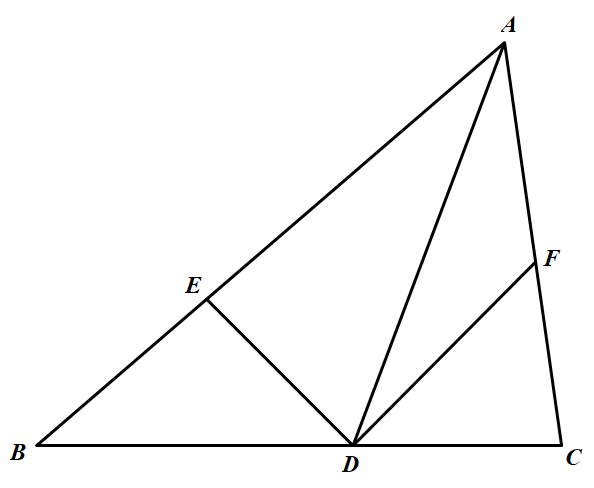
若在线段 $AB,AC$ 内存在点 $E,F$，满足 $B E=C F$ 和 $ \angle B D E=\angle C D F$，则因点 $D$ 和 $AB$ 和 $AC$ 的距离相等，所以，有 $S_{\triangle B D E}=S_{\triangle CDF}$ 从而有 $B D \cdot D E=D C \cdot D F$ ①
由余弦定理，有 $B D^{2}+D E^{2}-2 B D \cdot D E \cos \angle B D E=B E^{2}=C F^{2}=C D^{2}+D F^{2}-2 C D \cdot D F \cos \angle C D F$ ②
因 $\angle BDE =\angle GDF$，故由 ① 和 ②，可得
$B D^{2}+D E^{2}=C D^{2}+D F^{2}$ ③
$B D+D E=C D+D F$ ④
由 ① 和 ④ 可知下列两种情形之一成立
$\left\{\begin{array}{l}{B D=C D} \\ {D E=D F}\end{array}\right.$ ⑤
$\left\{\begin{array}{l}{B D=D F} \\ {D E=C D}\end{array}\right.$ ⑥
因 $b < c$，故式 ⑤ 不可能成立．所以，式 ⑥ 成立．从而 $\triangle D E B \cong \triangle D C F$ 进而有 $\angle B=\angle D F C, \angle C=\angle B E D$ 所以 $\angle B=\angle D F C>\angle D A F=\dfrac{1}{2} \angle A$ 即 $2 \angle B>\angle A$ 这是点 $E$ 和 $F$ 存在的必要条件．反之，若 $2\angle B >\angle A$，则
$\angle A D C=\angle B+\dfrac{1}{2} \angle A>\angle A,\angle A D B=\angle C+\dfrac{1}{2} \angle A>\angle A$
于是，可在 $\triangle ABC$ 内部作 $\angle B D E=\angle A, \angle C D F=\angle A$，且使点 $E$ 在 $AB$ 内，点 $F$ 在 $AC$ 内．这导致 $A,C,D,E$ 和 $A,B,D,F$ 都四点共圆．所以 $\angle B=\angle D F C$ 从而 $\triangle B D E \sim \triangle F D C$ 又因这两个三角形过点 $D$ 的高相等，所以 $\triangle B D E \cong \triangle F D C$．故 $B E=C F$ 综上可知，所求的充分必要条件是 $2\angle B>\angle A$．
（2）由（1）中论述知 $A, C, D, E$ 和 $A, B, D, F$ 都四点共圆．所以 $B E \cdot B A=B D \cdot B C, C F \cdot C A=C D \cdot C B$ 又因 $BE=CF$，所以 $B E(A B+A C)=B C(B D+D C)=B C^{2},B E=\dfrac{a^{2}}{b+c}$
若在线段 $AB,AC$ 内存在点 $E,F$，满足 $B E=C F$ 和 $ \angle B D E=\angle C D F$，则因点 $D$ 和 $AB$ 和 $AC$ 的距离相等，所以，有 $S_{\triangle B D E}=S_{\triangle CDF}$ 从而有 $B D \cdot D E=D C \cdot D F$ ①由余弦定理，有 $B D^{2}+D E^{2}-2 B D \cdot D E \cos \angle B D E=B E^{2}=C F^{2}=C D^{2}+D F^{2}-2 C D \cdot D F \cos \angle C D F$ ②
因 $\angle BDE =\angle GDF$，故由 ① 和 ②，可得
$B D^{2}+D E^{2}=C D^{2}+D F^{2}$ ③
$B D+D E=C D+D F$ ④
由 ① 和 ④ 可知下列两种情形之一成立
$\left\{\begin{array}{l}{B D=C D} \\ {D E=D F}\end{array}\right.$ ⑤
$\left\{\begin{array}{l}{B D=D F} \\ {D E=C D}\end{array}\right.$ ⑥
因 $b < c$，故式 ⑤ 不可能成立．所以，式 ⑥ 成立．从而 $\triangle D E B \cong \triangle D C F$ 进而有 $\angle B=\angle D F C, \angle C=\angle B E D$ 所以 $\angle B=\angle D F C>\angle D A F=\dfrac{1}{2} \angle A$ 即 $2 \angle B>\angle A$ 这是点 $E$ 和 $F$ 存在的必要条件．反之，若 $2\angle B >\angle A$，则
$\angle A D C=\angle B+\dfrac{1}{2} \angle A>\angle A,\angle A D B=\angle C+\dfrac{1}{2} \angle A>\angle A$
于是，可在 $\triangle ABC$ 内部作 $\angle B D E=\angle A, \angle C D F=\angle A$，且使点 $E$ 在 $AB$ 内，点 $F$ 在 $AC$ 内．这导致 $A,C,D,E$ 和 $A,B,D,F$ 都四点共圆．所以 $\angle B=\angle D F C$ 从而 $\triangle B D E \sim \triangle F D C$ 又因这两个三角形过点 $D$ 的高相等，所以 $\triangle B D E \cong \triangle F D C$．故 $B E=C F$ 综上可知，所求的充分必要条件是 $2\angle B>\angle A$．
（2）由（1）中论述知 $A, C, D, E$ 和 $A, B, D, F$ 都四点共圆．所以 $B E \cdot B A=B D \cdot B C, C F \cdot C A=C D \cdot C B$ 又因 $BE=CF$，所以 $B E(A B+A C)=B C(B D+D C)=B C^{2},B E=\dfrac{a^{2}}{b+c}$
答案
解析
备注
