对于平面上任意 4 个不同的点 $P_{1}, P_{2}, P_{3}, P_{4}$，求比值 $\displaystyle \dfrac{\sum\limits_{1\leqslant i<j\leqslant4 }P_iP_j}{\min\limits_{1\leqslant i<j\leqslant 4}P_iP_j}$ ① 的最小值．
【难度】
【出处】
2002第17届CMO试题
【标注】
【答案】
略
【解析】
先证如下的引理
引理：如图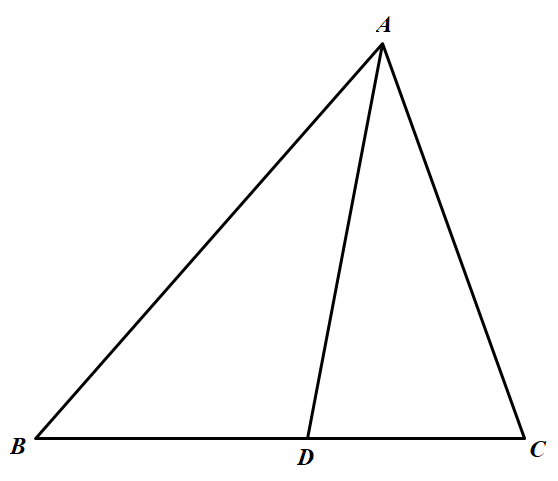
在 $\triangle ABC$ 中，若 $A B \geqslant m, A C \geqslant m, \angle B A C=\alpha$，则 $B C \geqslant 2 m \sin \frac{a}{2}$．
引理的证明：$\angle A $ 的平分线 $AD$，由正弦定理，有 $B C=B D+D C=A B \dfrac{\sin \angle BAD}{\sin\angle ADB } +A C \dfrac{\sin \angle C A D}{\sin \angle A D C}=\dfrac{\sin \dfrac{\alpha}{2}}{\sin \angle A D B}(A B+A C) \geqslant 2 m \sin \dfrac{\alpha}{2}$
回到原题的解．记 $\displaystyle m=\sum\limits_{1 \leqslant i<j\leqslant 4} P_{i} P_{j}, k=\sum_{1\leqslant i<j \leqslant 4} P_{i} P_{j}$，分类估计式 ① 的值．
（1）若 $P_{1}, P_{2}, P_{3}, P_{4}$ 中有 $3$ 点共线，不妨设前 $3$ 点共线，于是，有 $P_{1} P_{2}+P_{2} P_{3}+P_{1} P_{3} \geqslant 4 m$ 从而 $k \geqslant 7 m$ 故 $\dfrac{k}{m} \geqslant 7$
（2）若 $4$ 点的凸包是三角形，不妨设点 $P_{4}$ 在 $\triangle P_{1} P_{2} P_{3}$ 内部且 $\angle P_{1} P_{4} P_{2} \geqslant 120^{\circ}$．由引理知 $P_{1} P_{2} \geqslant 2 m \sin \dfrac{\angle P_{1} P_{4} P_{2}}{2} \geqslant 2 m \sin 60^{\circ}=\sqrt{3} m$ 从而 $\dfrac{k}{m} \geqslant 5+\sqrt{3}$ ②
（3）凸包是四边形 $P_{1} P_{2} P_{3} P_{4}$．若凸四边形 $P_{1} P_{2} P_{3} P_{4}$ 有一个内角不小于 $120^\circ$，不妨设为 $\angle P_{2} P_{1} P_{4}$，由引理有 $P_{2} P_{4} \geqslant \sqrt{3} m$．从而式 ② 成立．
设凸四边形 $P_{1} P_{2} P_{3} P_{4}$ 的 $ 4$ 个内角都小于 $120^\circ$ 如图所示．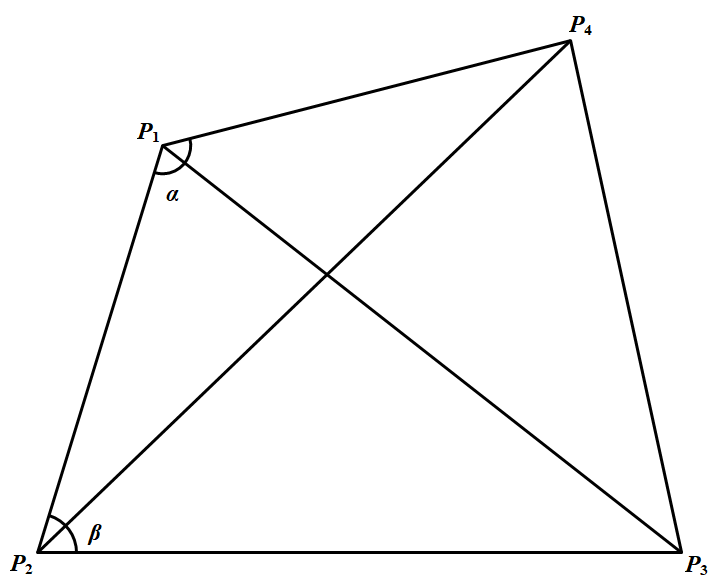
于是，总有两个相邻内角之和不小于 $ 180^\circ$．不妨设 $\alpha+\beta=\angle P_{4} P_{1} P_{2}+\angle P_{1} P_{2} P_{3} \geqslant 180^{\circ}$，且 $\alpha \geqslant \beta$．由于 $\alpha<120^{\circ}$，故 $\beta>60^\circ$．所以 $\dfrac{\alpha+\beta}{4} \geqslant 45^{\circ}, 0^{\circ} \leqslant \dfrac{\alpha-\beta}{4}<15^{\circ}$
由引理，有 $P_{2} P_{4} \geqslant 2 m \sin \dfrac{\alpha}{2}, P_{1} P_{3} \geqslant 2 m \sin \dfrac{\beta}{2}$ 则
$\begin{aligned} P_{1} P_{3}+P_{2} P_{4} \geqslant 2 m\left(\sin \frac{\alpha}{2}+\sin \frac{\beta}{2}\right) &= 4 m \sin \frac{\alpha+\beta}{4} \cos \frac{\alpha-\beta}{4} \geqslant 4 m \sin 45^{\circ} \cos 15^{\circ}= 2 m\left(\sin 60^{\circ}+\sin 30^{\circ}\right)=(\sqrt{3}+1) m \end{aligned}$
所以式 ② 成立．综上可知，在所有情况下，式 ② 均成立．
另一方面，当 $P_{1} P_{2} P_{3} P_{4}$ 是有一个内角为 $60^\circ$ 的菱形的 $4$ 个顶点时，式 ② 中等号成立．
所以所求的 $\dfrac{k}{m}$ 的最小值为 $5+\sqrt{3}$．
引理：如图
在 $\triangle ABC$ 中，若 $A B \geqslant m, A C \geqslant m, \angle B A C=\alpha$，则 $B C \geqslant 2 m \sin \frac{a}{2}$．引理的证明：$\angle A $ 的平分线 $AD$，由正弦定理，有 $B C=B D+D C=A B \dfrac{\sin \angle BAD}{\sin\angle ADB } +A C \dfrac{\sin \angle C A D}{\sin \angle A D C}=\dfrac{\sin \dfrac{\alpha}{2}}{\sin \angle A D B}(A B+A C) \geqslant 2 m \sin \dfrac{\alpha}{2}$
回到原题的解．记 $\displaystyle m=\sum\limits_{1 \leqslant i<j\leqslant 4} P_{i} P_{j}, k=\sum_{1\leqslant i<j \leqslant 4} P_{i} P_{j}$，分类估计式 ① 的值．
（1）若 $P_{1}, P_{2}, P_{3}, P_{4}$ 中有 $3$ 点共线，不妨设前 $3$ 点共线，于是，有 $P_{1} P_{2}+P_{2} P_{3}+P_{1} P_{3} \geqslant 4 m$ 从而 $k \geqslant 7 m$ 故 $\dfrac{k}{m} \geqslant 7$
（2）若 $4$ 点的凸包是三角形，不妨设点 $P_{4}$ 在 $\triangle P_{1} P_{2} P_{3}$ 内部且 $\angle P_{1} P_{4} P_{2} \geqslant 120^{\circ}$．由引理知 $P_{1} P_{2} \geqslant 2 m \sin \dfrac{\angle P_{1} P_{4} P_{2}}{2} \geqslant 2 m \sin 60^{\circ}=\sqrt{3} m$ 从而 $\dfrac{k}{m} \geqslant 5+\sqrt{3}$ ②
（3）凸包是四边形 $P_{1} P_{2} P_{3} P_{4}$．若凸四边形 $P_{1} P_{2} P_{3} P_{4}$ 有一个内角不小于 $120^\circ$，不妨设为 $\angle P_{2} P_{1} P_{4}$，由引理有 $P_{2} P_{4} \geqslant \sqrt{3} m$．从而式 ② 成立．
设凸四边形 $P_{1} P_{2} P_{3} P_{4}$ 的 $ 4$ 个内角都小于 $120^\circ$ 如图所示．
于是，总有两个相邻内角之和不小于 $ 180^\circ$．不妨设 $\alpha+\beta=\angle P_{4} P_{1} P_{2}+\angle P_{1} P_{2} P_{3} \geqslant 180^{\circ}$，且 $\alpha \geqslant \beta$．由于 $\alpha<120^{\circ}$，故 $\beta>60^\circ$．所以 $\dfrac{\alpha+\beta}{4} \geqslant 45^{\circ}, 0^{\circ} \leqslant \dfrac{\alpha-\beta}{4}<15^{\circ}$由引理，有 $P_{2} P_{4} \geqslant 2 m \sin \dfrac{\alpha}{2}, P_{1} P_{3} \geqslant 2 m \sin \dfrac{\beta}{2}$ 则
$\begin{aligned} P_{1} P_{3}+P_{2} P_{4} \geqslant 2 m\left(\sin \frac{\alpha}{2}+\sin \frac{\beta}{2}\right) &= 4 m \sin \frac{\alpha+\beta}{4} \cos \frac{\alpha-\beta}{4} \geqslant 4 m \sin 45^{\circ} \cos 15^{\circ}= 2 m\left(\sin 60^{\circ}+\sin 30^{\circ}\right)=(\sqrt{3}+1) m \end{aligned}$
所以式 ② 成立．综上可知，在所有情况下，式 ② 均成立．
另一方面，当 $P_{1} P_{2} P_{3} P_{4}$ 是有一个内角为 $60^\circ$ 的菱形的 $4$ 个顶点时，式 ② 中等号成立．
所以所求的 $\dfrac{k}{m}$ 的最小值为 $5+\sqrt{3}$．
答案
解析
备注
