一圆与 $\triangle ABC$ 的三边 $BC, CA,AB$ 的交点依次为 $D_1 ,D_2; E_1 ,E_2 ,F_1,F_2$．线段 $D_1E_1$ 与 $D_2F_2$ 交于点 $L$，线段 $E_1 F_1$ 与 $E_2D_2$ 交于点 $M$，线段 $F_1D_1 $ 与 $F_2E_2$ 交于点 $N$．证明：$AL,BM, CN$ 三线共点．
【难度】
【出处】
2005第20届CMO试题
【标注】
【答案】
略
【解析】
如图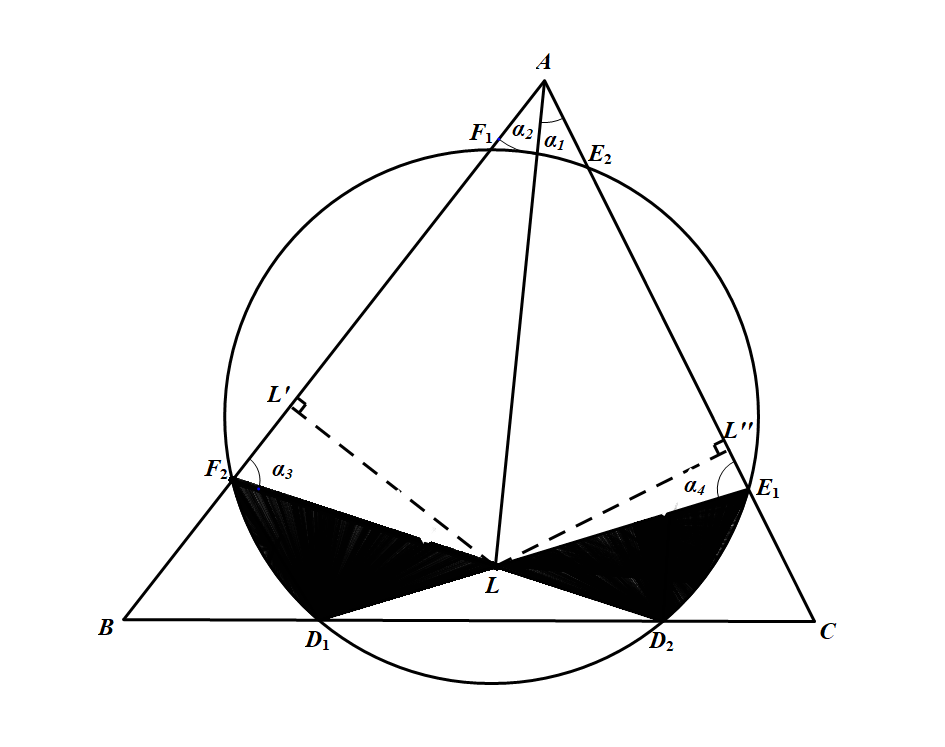
自点 $L$ 作 $AB$ 和 $AC$ 的垂线，垂足分别为 $L^\prime$ 和 $L^{\prime\prime}$．记 $\angle L A B=\alpha_{1}, \angle L A C=\alpha_{2}, \angle L F_{2} A=\alpha_{3}, \angle L E_{1} A=\alpha_{4}$．则有
$\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}}=\dfrac{L L^{\prime}}{L L^{\prime \prime}}=\dfrac{L F_{2} \sin \alpha_{3}}{L E_{1} \sin \alpha_{4}}$ ①
联结 $D_{1} F_{2}, D_{2} E_{1}$（上图）．由 $\triangle L D_{1} F_{2} \sim \triangle L D_{2} E_{1}$ 得 $\dfrac{L F_{2}}{L E_{1}}=\dfrac{D_{1} F_{2}}{D_{2} E_{1}}$ ②
联结 $D_{2} F_{1}, D_{1} E_{2}$（下图）．由正弦定理得 $\dfrac{\sin \alpha_{3}}{\sin \alpha_{4}}=\dfrac{D_{2} F_{1}}{D_{1} E_{2}}$ ③
将 ② 和 ③ 代入 ①，得到 $\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}}=\dfrac{D_{1} F_{2}}{D_{2} E_{1}} \cdot \dfrac{D_{2} F_{1}}{D_{1} E_{2}}$ ④
同理，记 $\angle M B C=\beta_{1}, \angle M B A=\beta_{2}, \angle N C A=\gamma_{1}, \angle N C B=\gamma_{2}$，可得
$\dfrac{\sin \beta_{1}}{\sin \beta_{2}}=\dfrac{E_{1} D_{2}}{E_{2} F_{1}} \cdot \dfrac{E_{2} D_{1}}{E_{1} F_{2}}$ ⑤
$\dfrac{\sin \gamma_{1}}{\sin \gamma_{2}}=\dfrac{F_{1} E_{2}}{F_{2} D_{1}} \cdot \dfrac{F_{2} E_{1}}{F_{1} D_{2}}$ ⑥
将 ④，⑤，⑥ 式相乘，得 $\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}} \cdot \dfrac{\sin \beta_{1}}{\sin \beta_{2}} \cdot \dfrac{\sin \gamma_{1}}{\sin \gamma_{2}}=1$
由塞瓦定理的逆定理，即知 $AL, BM, CN$ 三线共点．
自点 $L$ 作 $AB$ 和 $AC$ 的垂线，垂足分别为 $L^\prime$ 和 $L^{\prime\prime}$．记 $\angle L A B=\alpha_{1}, \angle L A C=\alpha_{2}, \angle L F_{2} A=\alpha_{3}, \angle L E_{1} A=\alpha_{4}$．则有$\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}}=\dfrac{L L^{\prime}}{L L^{\prime \prime}}=\dfrac{L F_{2} \sin \alpha_{3}}{L E_{1} \sin \alpha_{4}}$ ①
联结 $D_{1} F_{2}, D_{2} E_{1}$（上图）．由 $\triangle L D_{1} F_{2} \sim \triangle L D_{2} E_{1}$ 得 $\dfrac{L F_{2}}{L E_{1}}=\dfrac{D_{1} F_{2}}{D_{2} E_{1}}$ ②
联结 $D_{2} F_{1}, D_{1} E_{2}$（下图）．由正弦定理得 $\dfrac{\sin \alpha_{3}}{\sin \alpha_{4}}=\dfrac{D_{2} F_{1}}{D_{1} E_{2}}$ ③
将 ② 和 ③ 代入 ①，得到 $\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}}=\dfrac{D_{1} F_{2}}{D_{2} E_{1}} \cdot \dfrac{D_{2} F_{1}}{D_{1} E_{2}}$ ④同理，记 $\angle M B C=\beta_{1}, \angle M B A=\beta_{2}, \angle N C A=\gamma_{1}, \angle N C B=\gamma_{2}$，可得
$\dfrac{\sin \beta_{1}}{\sin \beta_{2}}=\dfrac{E_{1} D_{2}}{E_{2} F_{1}} \cdot \dfrac{E_{2} D_{1}}{E_{1} F_{2}}$ ⑤
$\dfrac{\sin \gamma_{1}}{\sin \gamma_{2}}=\dfrac{F_{1} E_{2}}{F_{2} D_{1}} \cdot \dfrac{F_{2} E_{1}}{F_{1} D_{2}}$ ⑥
将 ④，⑤，⑥ 式相乘，得 $\dfrac{\sin \alpha_{1}}{\sin \alpha_{2}} \cdot \dfrac{\sin \beta_{1}}{\sin \beta_{2}} \cdot \dfrac{\sin \gamma_{1}}{\sin \gamma_{2}}=1$
由塞瓦定理的逆定理，即知 $AL, BM, CN$ 三线共点．
答案
解析
备注
