在 $\mathrm{Rt} \triangle A B C$ 中，$\angle ACB=90^\circ,\triangle ABC$，的内切圆 $O$ 分别于与 $BC, CA ,AB$ 相切于点 $D,E,F$，联结 $AD$，与内切圆 $O$ 相交于点 $P$．联结 $BP,CP$，若 $\angle B P C=90^{\circ}$，求证：$ AE +AP= PD$．
【难度】
【出处】
2006第21届CMO试题
【标注】
【答案】
略
【解析】
设 $AE= AF = x , BD = B F = y, CD = CE = z,AP= m,PD = n$．因为 $\angle A C P+\angle P C B=90^{\circ}=\angle P B C+\angle P C B$，所以 $\angle A C P=\angle P B C$．如图所示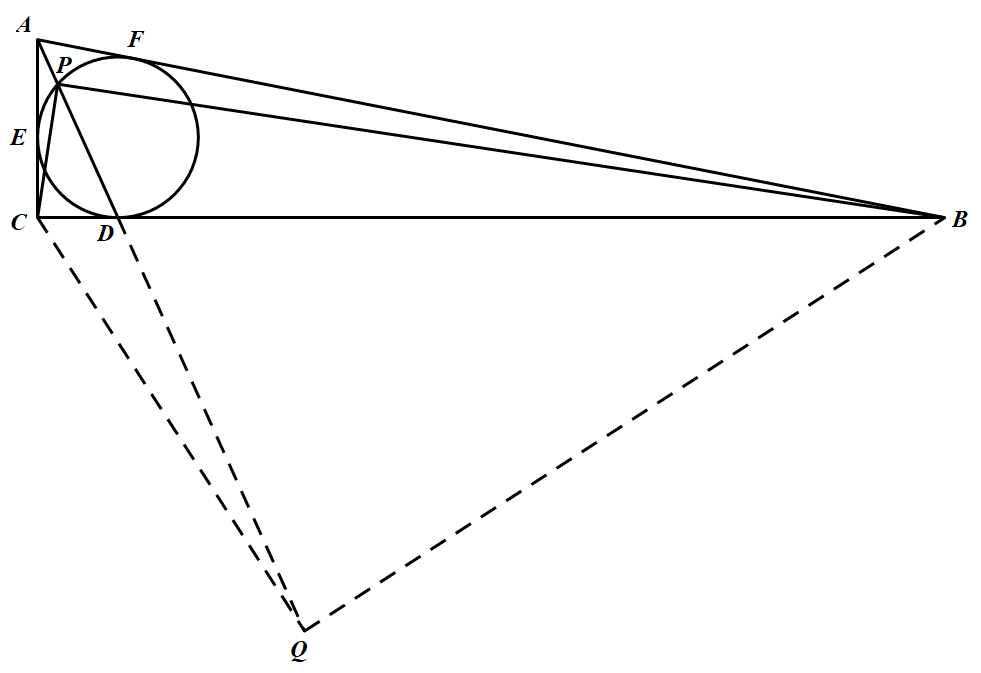
延长 $AD$ 至点 $Q$，使得 $\angle A Q C=\angle A C P=\angle P B C$，联结 $BQ,CQ$，则 $P,B,Q,C$ 四点共圆，令 $DQ= l$，则由相交弦定理和切割线定理可得
$y z=n l$ ①
$x^{2}=m(m+n)$ ②
因为 $\triangle A C P \sim \triangle A Q C$，所以 $\dfrac{A C}{A Q}=\dfrac{A P}{A C}$，故 $(x +z)^{2}=m(m+n+l)$ ③
在 $Rt\triangle ACD$ 和 $Rt\triangle ACB$ 中 由勾股定理得
$(x+z)^{2}+z^{2}=(m+n)^{2}$ ④
$(y+z)^{2}+(z+x)^{2}=(x+y)^{2}$ ⑤
③ - ② 得 $z^{2}+2 z x=m l$ ⑥
① $\div$ ⑥，得 $\dfrac{y z}{z^{2}+2 z x}=\dfrac{n}{m}$ 所以 $1+\frac{y z}{z^{2}+2 z x}=\frac{m+n}{m}$ ⑦
② $\times$ ⑦，结合 ④，得 $x^{2}+\dfrac{x^{2} y z}{z^{2}+2 z x}=(m+n)^{2}=(x+z)^{2}+z^{2}$ 整理得
$\dfrac{x^{2} y}{z+2 x}=2 z(x+z)$ ⑧
又式 ⑤ 可写为 $x+z=\dfrac{2 x y}{y+z}$ ⑨
由 ⑧，⑨ 得 $\dfrac{x}{z+2 x}=\dfrac{4 z}{y+z}$ ⑩
又式 ⑤ 还可写为 $y+z=\dfrac{2 x z}{x-z}$ ⑪
把上式代入⑩，消去 $y + z$，得 $3 x^{2}-2 x z-2 z^{2}=0$
解得 $x=\dfrac{\sqrt{7}+1}{3} z$
代入 ④，得 $m+n=\dfrac{2(\sqrt{7}+1)}{3} z$
结合 ②，得 $m=\dfrac{x^{2}}{m+n}=\dfrac{\sqrt{7}+1}{6} z$
从而 $n=\dfrac{\sqrt{7}+1}{2} z$
所以，$ x + m = n$，即 $AE+AP= PD$．
延长 $AD$ 至点 $Q$，使得 $\angle A Q C=\angle A C P=\angle P B C$，联结 $BQ,CQ$，则 $P,B,Q,C$ 四点共圆，令 $DQ= l$，则由相交弦定理和切割线定理可得$y z=n l$ ①
$x^{2}=m(m+n)$ ②
因为 $\triangle A C P \sim \triangle A Q C$，所以 $\dfrac{A C}{A Q}=\dfrac{A P}{A C}$，故 $(x +z)^{2}=m(m+n+l)$ ③
在 $Rt\triangle ACD$ 和 $Rt\triangle ACB$ 中 由勾股定理得
$(x+z)^{2}+z^{2}=(m+n)^{2}$ ④
$(y+z)^{2}+(z+x)^{2}=(x+y)^{2}$ ⑤
③ - ② 得 $z^{2}+2 z x=m l$ ⑥
① $\div$ ⑥，得 $\dfrac{y z}{z^{2}+2 z x}=\dfrac{n}{m}$ 所以 $1+\frac{y z}{z^{2}+2 z x}=\frac{m+n}{m}$ ⑦
② $\times$ ⑦，结合 ④，得 $x^{2}+\dfrac{x^{2} y z}{z^{2}+2 z x}=(m+n)^{2}=(x+z)^{2}+z^{2}$ 整理得
$\dfrac{x^{2} y}{z+2 x}=2 z(x+z)$ ⑧
又式 ⑤ 可写为 $x+z=\dfrac{2 x y}{y+z}$ ⑨
由 ⑧，⑨ 得 $\dfrac{x}{z+2 x}=\dfrac{4 z}{y+z}$ ⑩
又式 ⑤ 还可写为 $y+z=\dfrac{2 x z}{x-z}$ ⑪
把上式代入⑩，消去 $y + z$，得 $3 x^{2}-2 x z-2 z^{2}=0$
解得 $x=\dfrac{\sqrt{7}+1}{3} z$
代入 ④，得 $m+n=\dfrac{2(\sqrt{7}+1)}{3} z$
结合 ②，得 $m=\dfrac{x^{2}}{m+n}=\dfrac{\sqrt{7}+1}{6} z$
从而 $n=\dfrac{\sqrt{7}+1}{2} z$
所以，$ x + m = n$，即 $AE+AP= PD$．
答案
解析
备注
