在面积为 $1$ 的矩形 $ABCD$ 中(包括边界)有 $5$ 个点,其中任意三点不共线求以这 $5$ 个点为顶点的所有三角形中,面积不大于 $\dfrac{1}{4}$ 的三角形的个数的最小值 $4$.
【难度】
【出处】
2005第20届CMO试题
【标注】
【答案】
略
【解析】
本题证明需要用到如下的常用结论,我们将其作为一个引理:矩形内的任意一个三角形的面积不大于矩形面积的一半.
在矩形 $ABCD$ 中,如果某三点构成的三角形的面积不大于 $\dfrac{1}{4}$ 就称它们为一个好的三点组,简称为“好组".
记 $AB,CD,BC,AD$ 的中点分别为 $E,F,H,G$,线段 $EF$ 与 $CH$ 的交点记为 $O$.线段 $EF$ 和 $GH$ 将矩形 $ABCD$ 分为四个小矩形.从而一定存在一个小矩形,不妨设为 $AEOG$,其中(包括边界,下同)至少有所给 $5$ 个点中的 $2$ 个点,设点 $M$ 和 $N$ 在小矩形 $AEOG$ 中,如图所示.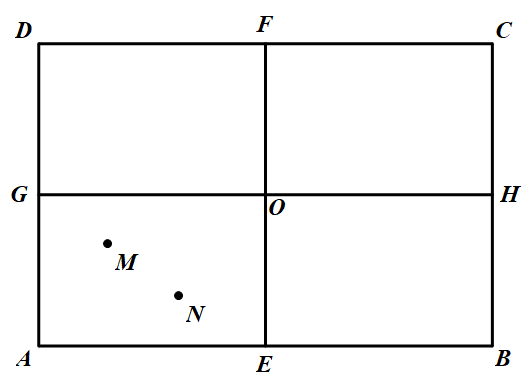 (1)如果矩形 $OHCF$ 中有不多于 $ 1$ 个已知点,考察不在矩形 $OHCF$ 中的任意一个 不同于 $M$ 和 $N$ 的已知点 $X$.易知,三点组 $(M,N,X)$ 或者在矩形 $ ABH G$ 中,或者在矩形 $ AEFD$ 中,由引理可知 $(M,N,X)$ 是好组.由于这样的点 $X$ 至少有两个,所以至少有两个好组.
(1)如果矩形 $OHCF$ 中有不多于 $ 1$ 个已知点,考察不在矩形 $OHCF$ 中的任意一个 不同于 $M$ 和 $N$ 的已知点 $X$.易知,三点组 $(M,N,X)$ 或者在矩形 $ ABH G$ 中,或者在矩形 $ AEFD$ 中,由引理可知 $(M,N,X)$ 是好组.由于这样的点 $X$ 至少有两个,所以至少有两个好组.
(2)如果矩形 $OHCF$ 中至少有 $2$ 个已知点,不妨设已知点 $P$ 和 $Q$ 都在矩形 $OHCF$ 中,考察剩下来的最后一个已知点 $R$.如果 $R$ 在矩形 $OFDG$ 中,则三点组 $ (M,N,R)$ 在矩形 $ AEFD$ 中,而三点组 $(P,Q,R)$ 在矩形 $GHCD$ 中,从而它们都是好组,于是至少有两个好组.同理,如果点 $R$ 在矩形 $EBHO$ 中,亦至少有两个好组如果点 $R$ 在矩形 $OHCF$ 或矩形 $AEOG$ 中,设点 $R$ 在矩形 $OHCF$ 中,我们来考察 $5$ 个 点 $M,N,P,Q,R$ 的凸包,该凸包一定在凸六边形 $AEHCFG$ 中,如图所示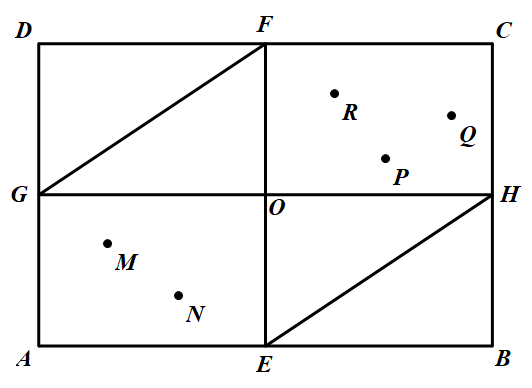 而 $S_{AEHCFG}=1-\dfrac{1}{8}-\dfrac{1}{8}=\dfrac{3}{4}$
而 $S_{AEHCFG}=1-\dfrac{1}{8}-\dfrac{1}{8}=\dfrac{3}{4}$
下面再分三种情况讨论:
(i)如果 $M,N,P,Q,R$ 的凸包是凸五边形,不妨设其为 $MNPQR$,如图所示 此时 $S_{MQR}+S_{MNQ}+S_{NPQ}\geqslant \dfrac{3}{4}$ 从而 $(M,Q, R ) , (M, N, Q ) , (N,P, Q )$ 中至少有一个为好组.又由于 $(P,Q,R)$ 在矩形 $OHCF$ 中,当然是好组,所以至少有两个好组.
此时 $S_{MQR}+S_{MNQ}+S_{NPQ}\geqslant \dfrac{3}{4}$ 从而 $(M,Q, R ) , (M, N, Q ) , (N,P, Q )$ 中至少有一个为好组.又由于 $(P,Q,R)$ 在矩形 $OHCF$ 中,当然是好组,所以至少有两个好组.
(ii)如果 $M,N,P,Q,R$ 的凸包是凸四边形,不妨其设为 $A_1A_2A_3A_4$,而另一个已知点为 $A_5$,如图所示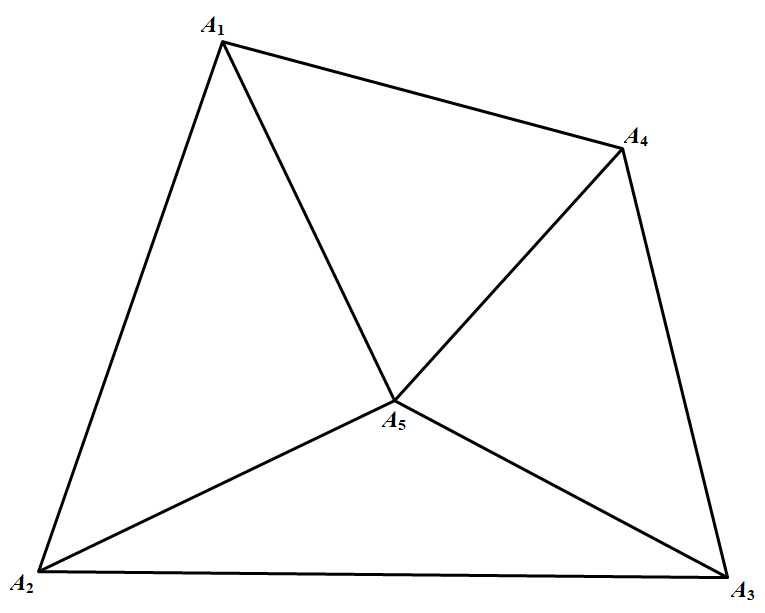 其中 $A_i\in \{M,N,P,Q,R\}(i = 1,2,3,4,5)$.联结 $A_5A_i(i = 1,2,3 ,4)$,则 ${{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{3}}}{{A}_{\text{4}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{4}}}{{A}_{\text{1}}}{{A}_{\text{5}}}}}\text{=}{{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{4}}}}}\leqslant \dfrac{\text{3}}{\text{4}}$
其中 $A_i\in \{M,N,P,Q,R\}(i = 1,2,3,4,5)$.联结 $A_5A_i(i = 1,2,3 ,4)$,则 ${{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{3}}}{{A}_{\text{4}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{4}}}{{A}_{\text{1}}}{{A}_{\text{5}}}}}\text{=}{{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{4}}}}}\leqslant \dfrac{\text{3}}{\text{4}}$
从而 $\left(A_{1}, A_{2}, A_{5}\right),\left(A_{2}, A_{3}, A_{5}\right),\left(A_{3}, A_{4}, A_{5}\right),\left(A_{1}, A_{4}, A_{5}\right)$ 中至少有两个好组.
(iii)若 $M,N,P,Q,R$ 的凸包是一个三角形,不妨设其为 $\triangle A_{1} A_{2} A_{3}$,另外两个已知点为 $A_4 ,A_5$,如图所示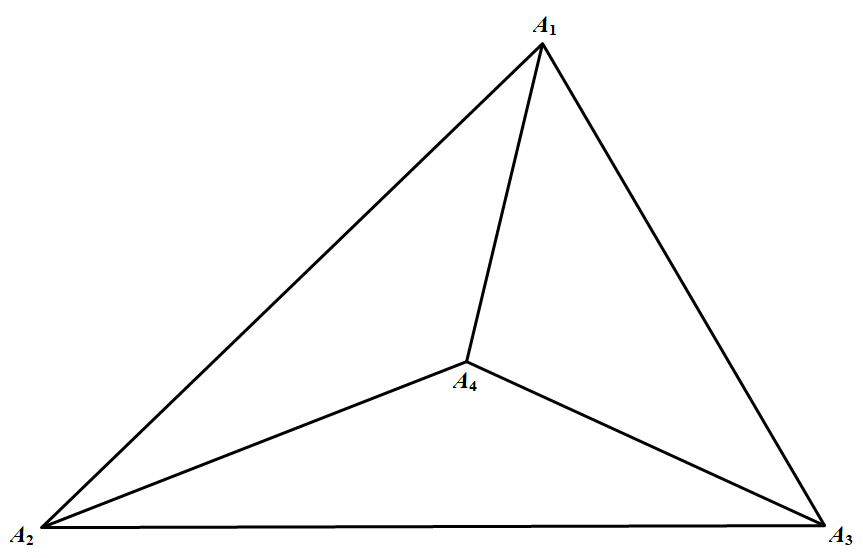 其中 $A_i\in\{M, N, P, Q, R\}(i=1,2,3,4,5)$.联结 $A_{4} A_{i}(i=1,2,3)$ 则 $S_{\triangle A_{1} A_{2} A_{4}}+S_{\Delta \Lambda_{2} A_{3} A_{4}}+S_{\triangle A_{1} A_{1} A_{4}}=S_{\triangle A_{1} A_{2} A_{3}} \leqslant \frac{3}{4}$
其中 $A_i\in\{M, N, P, Q, R\}(i=1,2,3,4,5)$.联结 $A_{4} A_{i}(i=1,2,3)$ 则 $S_{\triangle A_{1} A_{2} A_{4}}+S_{\Delta \Lambda_{2} A_{3} A_{4}}+S_{\triangle A_{1} A_{1} A_{4}}=S_{\triangle A_{1} A_{2} A_{3}} \leqslant \frac{3}{4}$
从而 $\left(A_{1}, A_{2}, A_{4}\right),\left(A_{2}, A_{3}, A_{4}\right),\left(A_{1}, A_{3}, A_{4}\right)$ 中至少有一个好组.同理,$A_5$ 也与 $A_1,A_2,A_3$ 中的某两个点构成好组,所以此时也至少有两个好组.
综上所述,不论何种情况,在 $5$ 个已知点中都至少有两个好组.
下面我们给出例子说明好组的数目可以只有两个.在矩形 $ABCD$ 的边 $AD$ 上取一点 $M$,在边 $AB$ 上取一点 $N$.使得 $AN:NB=AM:MD = 2 : 3$,如图所示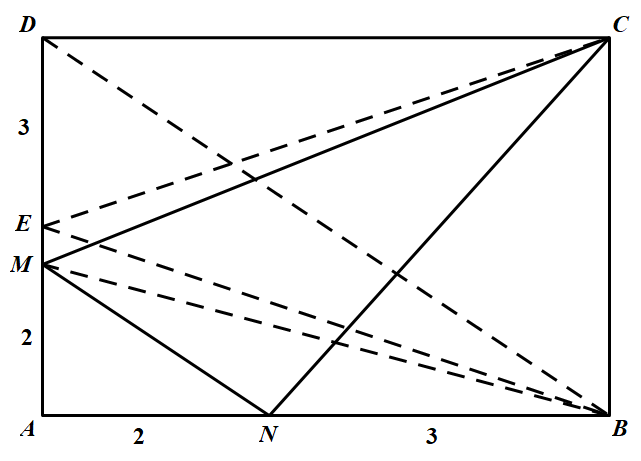 则在 $M,N,B,C,D$ 这 $5$ 个点中恰好有两个好组.事实上,$(B,C,D)$ 显然不是好组.而如果三点组中恰含 $M,N$ 两点之一,不妨设含点 $M$,设 $AD$ 的中点为 $E$,那么 $S_{\triangle M B D}=S_{\Delta E B D}=\dfrac{1}{4}$,所以 $(M,B,D)$ 不是好组,并且 $S_{\triangle M B C}=\dfrac{1}{2}, S_{\Delta M C D}>S_{\Delta E C D}=\dfrac{1}{4}$
则在 $M,N,B,C,D$ 这 $5$ 个点中恰好有两个好组.事实上,$(B,C,D)$ 显然不是好组.而如果三点组中恰含 $M,N$ 两点之一,不妨设含点 $M$,设 $AD$ 的中点为 $E$,那么 $S_{\triangle M B D}=S_{\Delta E B D}=\dfrac{1}{4}$,所以 $(M,B,D)$ 不是好组,并且 $S_{\triangle M B C}=\dfrac{1}{2}, S_{\Delta M C D}>S_{\Delta E C D}=\dfrac{1}{4}$
从而 $(M,B,C),(M,C,D)$ 都不是好组.如果三点组中同时含有 $M,N$ 两点,那么 $S_{\triangle M N C}=1-S_{\triangle N B C}-S_{\triangle M C D}-S_{\triangle A M N}=1-\dfrac{3}{5} S_{\Delta A B C}-\dfrac{3}{5} S_{\triangle A C D}-\dfrac{4}{25} S_{\Delta A B D}=1-\dfrac{3}{10}-\dfrac{3}{10}-\dfrac{2}{25}=\dfrac{8}{25}>\dfrac{1}{4}$
所以 $(M, N, C)$ 不是好组,而 $S_{\Delta M N B}=S_{\triangle M N D}=\dfrac{1}{5}<\dfrac{1}{4}$.从而其中恰好有两个好组 $(M,N,B)$ 和 $(M,N,D)$.
故面积不大于 $\dfrac{1}{4}$ 的三角形的个数的最小值是 $2$.
在矩形 $ABCD$ 中,如果某三点构成的三角形的面积不大于 $\dfrac{1}{4}$ 就称它们为一个好的三点组,简称为“好组".
记 $AB,CD,BC,AD$ 的中点分别为 $E,F,H,G$,线段 $EF$ 与 $CH$ 的交点记为 $O$.线段 $EF$ 和 $GH$ 将矩形 $ABCD$ 分为四个小矩形.从而一定存在一个小矩形,不妨设为 $AEOG$,其中(包括边界,下同)至少有所给 $5$ 个点中的 $2$ 个点,设点 $M$ 和 $N$ 在小矩形 $AEOG$ 中,如图所示.
 (1)如果矩形 $OHCF$ 中有不多于 $ 1$ 个已知点,考察不在矩形 $OHCF$ 中的任意一个 不同于 $M$ 和 $N$ 的已知点 $X$.易知,三点组 $(M,N,X)$ 或者在矩形 $ ABH G$ 中,或者在矩形 $ AEFD$ 中,由引理可知 $(M,N,X)$ 是好组.由于这样的点 $X$ 至少有两个,所以至少有两个好组.
(1)如果矩形 $OHCF$ 中有不多于 $ 1$ 个已知点,考察不在矩形 $OHCF$ 中的任意一个 不同于 $M$ 和 $N$ 的已知点 $X$.易知,三点组 $(M,N,X)$ 或者在矩形 $ ABH G$ 中,或者在矩形 $ AEFD$ 中,由引理可知 $(M,N,X)$ 是好组.由于这样的点 $X$ 至少有两个,所以至少有两个好组.(2)如果矩形 $OHCF$ 中至少有 $2$ 个已知点,不妨设已知点 $P$ 和 $Q$ 都在矩形 $OHCF$ 中,考察剩下来的最后一个已知点 $R$.如果 $R$ 在矩形 $OFDG$ 中,则三点组 $ (M,N,R)$ 在矩形 $ AEFD$ 中,而三点组 $(P,Q,R)$ 在矩形 $GHCD$ 中,从而它们都是好组,于是至少有两个好组.同理,如果点 $R$ 在矩形 $EBHO$ 中,亦至少有两个好组如果点 $R$ 在矩形 $OHCF$ 或矩形 $AEOG$ 中,设点 $R$ 在矩形 $OHCF$ 中,我们来考察 $5$ 个 点 $M,N,P,Q,R$ 的凸包,该凸包一定在凸六边形 $AEHCFG$ 中,如图所示
 而 $S_{AEHCFG}=1-\dfrac{1}{8}-\dfrac{1}{8}=\dfrac{3}{4}$
而 $S_{AEHCFG}=1-\dfrac{1}{8}-\dfrac{1}{8}=\dfrac{3}{4}$下面再分三种情况讨论:
(i)如果 $M,N,P,Q,R$ 的凸包是凸五边形,不妨设其为 $MNPQR$,如图所示
 此时 $S_{MQR}+S_{MNQ}+S_{NPQ}\geqslant \dfrac{3}{4}$ 从而 $(M,Q, R ) , (M, N, Q ) , (N,P, Q )$ 中至少有一个为好组.又由于 $(P,Q,R)$ 在矩形 $OHCF$ 中,当然是好组,所以至少有两个好组.
此时 $S_{MQR}+S_{MNQ}+S_{NPQ}\geqslant \dfrac{3}{4}$ 从而 $(M,Q, R ) , (M, N, Q ) , (N,P, Q )$ 中至少有一个为好组.又由于 $(P,Q,R)$ 在矩形 $OHCF$ 中,当然是好组,所以至少有两个好组.(ii)如果 $M,N,P,Q,R$ 的凸包是凸四边形,不妨其设为 $A_1A_2A_3A_4$,而另一个已知点为 $A_5$,如图所示
 其中 $A_i\in \{M,N,P,Q,R\}(i = 1,2,3,4,5)$.联结 $A_5A_i(i = 1,2,3 ,4)$,则 ${{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{3}}}{{A}_{\text{4}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{4}}}{{A}_{\text{1}}}{{A}_{\text{5}}}}}\text{=}{{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{4}}}}}\leqslant \dfrac{\text{3}}{\text{4}}$
其中 $A_i\in \{M,N,P,Q,R\}(i = 1,2,3,4,5)$.联结 $A_5A_i(i = 1,2,3 ,4)$,则 ${{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{3}}}{{A}_{\text{4}}}{{A}_{\text{5}}}}}\text{+}{{S}_{\vartriangle{{A}_{\text{4}}}{{A}_{\text{1}}}{{A}_{\text{5}}}}}\text{=}{{S}_{\vartriangle{{A}_{1}}{{A}_{\text{2}}}{{A}_{\text{3}}}{{A}_{\text{4}}}}}\leqslant \dfrac{\text{3}}{\text{4}}$从而 $\left(A_{1}, A_{2}, A_{5}\right),\left(A_{2}, A_{3}, A_{5}\right),\left(A_{3}, A_{4}, A_{5}\right),\left(A_{1}, A_{4}, A_{5}\right)$ 中至少有两个好组.
(iii)若 $M,N,P,Q,R$ 的凸包是一个三角形,不妨设其为 $\triangle A_{1} A_{2} A_{3}$,另外两个已知点为 $A_4 ,A_5$,如图所示
 其中 $A_i\in\{M, N, P, Q, R\}(i=1,2,3,4,5)$.联结 $A_{4} A_{i}(i=1,2,3)$ 则 $S_{\triangle A_{1} A_{2} A_{4}}+S_{\Delta \Lambda_{2} A_{3} A_{4}}+S_{\triangle A_{1} A_{1} A_{4}}=S_{\triangle A_{1} A_{2} A_{3}} \leqslant \frac{3}{4}$
其中 $A_i\in\{M, N, P, Q, R\}(i=1,2,3,4,5)$.联结 $A_{4} A_{i}(i=1,2,3)$ 则 $S_{\triangle A_{1} A_{2} A_{4}}+S_{\Delta \Lambda_{2} A_{3} A_{4}}+S_{\triangle A_{1} A_{1} A_{4}}=S_{\triangle A_{1} A_{2} A_{3}} \leqslant \frac{3}{4}$从而 $\left(A_{1}, A_{2}, A_{4}\right),\left(A_{2}, A_{3}, A_{4}\right),\left(A_{1}, A_{3}, A_{4}\right)$ 中至少有一个好组.同理,$A_5$ 也与 $A_1,A_2,A_3$ 中的某两个点构成好组,所以此时也至少有两个好组.
综上所述,不论何种情况,在 $5$ 个已知点中都至少有两个好组.
下面我们给出例子说明好组的数目可以只有两个.在矩形 $ABCD$ 的边 $AD$ 上取一点 $M$,在边 $AB$ 上取一点 $N$.使得 $AN:NB=AM:MD = 2 : 3$,如图所示
 则在 $M,N,B,C,D$ 这 $5$ 个点中恰好有两个好组.事实上,$(B,C,D)$ 显然不是好组.而如果三点组中恰含 $M,N$ 两点之一,不妨设含点 $M$,设 $AD$ 的中点为 $E$,那么 $S_{\triangle M B D}=S_{\Delta E B D}=\dfrac{1}{4}$,所以 $(M,B,D)$ 不是好组,并且 $S_{\triangle M B C}=\dfrac{1}{2}, S_{\Delta M C D}>S_{\Delta E C D}=\dfrac{1}{4}$
则在 $M,N,B,C,D$ 这 $5$ 个点中恰好有两个好组.事实上,$(B,C,D)$ 显然不是好组.而如果三点组中恰含 $M,N$ 两点之一,不妨设含点 $M$,设 $AD$ 的中点为 $E$,那么 $S_{\triangle M B D}=S_{\Delta E B D}=\dfrac{1}{4}$,所以 $(M,B,D)$ 不是好组,并且 $S_{\triangle M B C}=\dfrac{1}{2}, S_{\Delta M C D}>S_{\Delta E C D}=\dfrac{1}{4}$从而 $(M,B,C),(M,C,D)$ 都不是好组.如果三点组中同时含有 $M,N$ 两点,那么 $S_{\triangle M N C}=1-S_{\triangle N B C}-S_{\triangle M C D}-S_{\triangle A M N}=1-\dfrac{3}{5} S_{\Delta A B C}-\dfrac{3}{5} S_{\triangle A C D}-\dfrac{4}{25} S_{\Delta A B D}=1-\dfrac{3}{10}-\dfrac{3}{10}-\dfrac{2}{25}=\dfrac{8}{25}>\dfrac{1}{4}$
所以 $(M, N, C)$ 不是好组,而 $S_{\Delta M N B}=S_{\triangle M N D}=\dfrac{1}{5}<\dfrac{1}{4}$.从而其中恰好有两个好组 $(M,N,B)$ 和 $(M,N,D)$.
故面积不大于 $\dfrac{1}{4}$ 的三角形的个数的最小值是 $2$.
答案
解析
备注