在正 $n$ 边形的每个顶点上各停有 $1$ 只喜鹊，偶受惊吓使得众喜鹊都飞去，一段时间后，它们又都回到这些点上，仍是每个顶点上 $1$ 只，但未必都回到原来的顶点．求所有正整数 $n
$，使得一定存在 $3$ 只喜鹊，以它们前后所在的顶点分别形成的三角形或同为锐角三角形，或同为直角三角形，或同为钝角三角形．
$，使得一定存在 $3$ 只喜鹊，以它们前后所在的顶点分别形成的三角形或同为锐角三角形，或同为直角三角形，或同为钝角三角形．
【难度】
【出处】
2001第16届CMO试题
【标注】
【答案】
略
【解析】
解法一
当 $n= 3,4$ 时，结论显然成立．
当 $n = 5$ 时，连出 $5$ 条对角线的正五边形中，恰有钝角三角形与锐角三角形各 $5$ 个．当 $5$ 只喜鹊 $A,B,C,D,E$ 飞落前后的状态如图所示时，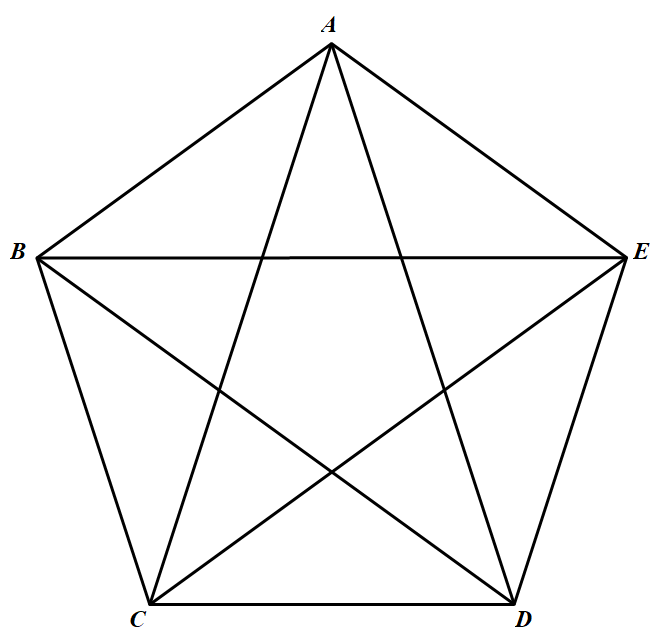
锐角三角形与钝角三角形互变，不满足题中要求．故知 $n= 5$ 不行．
当 $n=2 m, m \geqslant 3, m \in N$ 时，取正 $n$ 边形的一对相对顶点 $A$ 和 $B$ 并考察从这两点飞起的两只喜鹊（仍称之为 $A$ 和 $B$）的落点．若喜鹊 $A$ 和 $B$ 的落点仍是一对相对顶点，则可任取另一只喜鹊 $C$，于是，$A,B,C$ 三只喜鹊飞落前后所占据的项点都构成直角三角形．若喜鹊 $A$ 和 $B$ 的落点 $A^{\prime},B^\prime$ 不是相对顶点，则可记 $A^\prime$ 的相对顶点为 $C^\prime$ 并记返回后落在 $C^\prime$ 的喜鹊是从点C飞起的．于是，$A, B,C$ 三只喜鹊飞落前后所占据的顶点都构成直角三角形．这就证明了所有不小于 $4$ 的偶数 $n$ 都满足要求．
设 $n=2 m+1, m \geqslant 3, m \in \mathbf{N}$．这时图中没有直角三角形，让我们来证明如下引理．
引理：当 $n=2 m+1, m \geqslant 3$ 时，连出所有对角线的正 $n$ 边形中，钝角三角形的个数多千所有三角形个数的一半．
引理的证明：设正 $n$ 边形为 $A_{1} A_{2} \cdots A_{n}$．这时，以对角线 $A_{1} A_{j+1}$ 为最长边的钝角三角形的个数为 $j -1$．所以钝角三角形的总数为 $S=(2 m+1)(1+2+\cdots+(m-1))=\frac{1}{2}(2 m+1) m(m-1)$ 正 $n$ 边形中三角形总数为 $t=C_{n}^{3}=\frac{1}{3}(2 m+1) m(2 m-1)$ 因为 $\begin{aligned} m-1>\frac{1}{3}(2 m-1) \Leftrightarrow & 3 m-3>2 m-1 \Leftrightarrow m>3-1=2 \end{aligned}$
后者显然成立，故知引理成立．
由引理可知，当 $n= 2m + 1,m\geqslant 3$ 时，总存在 $3$ 只喜鹊，它们飞落前后所在的 $3$ 个顶点都构成钝角三角形．这表明不小于 $7$ 的所有奇数都满足题中的要求．
综上可知，满足题中要求的所有自然数是 $n \geqslant 3, n \neq 5$
解法二
前面证明均同解法一，只是将 $n= 2m + 1,m \geqslant 3$ 的情形改证如下．
由于将正 $n$ 边形连同顶点上落的峉鹊一起旋转时，三角形的形状不变，故可假设一只喜鹊 $A$ 飞走后返回时仍然落在原处．过 $A$ 所在的顶点作正 $n$ 边形的外接圆的一条直径 $AA^\prime$，于是，这条直径两侧各有 $m$ 只喜鹊．易见，位于直径同侧的任何两只喜鹊与 $A$ 一起所在的 $3$ 个顶点都构成钝角三角形．由于 $m\geqslant 3$，所以位于直径同侧的 $m$ 只喜鹊中，飞走返回时总有两只 $B$ 和 $C$ 仍在直径的同一侧，于是，$A,B,C$ 这三只喜鹊飞落前后所在的 $3$ 个顶点都构成钝角三角形．这就证明了不小于 $7$ 的所有奇数都满足题中的要求，所以满足题中要求的所有自然数就是 $n\geqslant 3,n\ne 65$．
当 $n= 3,4$ 时，结论显然成立．
当 $n = 5$ 时，连出 $5$ 条对角线的正五边形中，恰有钝角三角形与锐角三角形各 $5$ 个．当 $5$ 只喜鹊 $A,B,C,D,E$ 飞落前后的状态如图所示时，
锐角三角形与钝角三角形互变，不满足题中要求．故知 $n= 5$ 不行．当 $n=2 m, m \geqslant 3, m \in N$ 时，取正 $n$ 边形的一对相对顶点 $A$ 和 $B$ 并考察从这两点飞起的两只喜鹊（仍称之为 $A$ 和 $B$）的落点．若喜鹊 $A$ 和 $B$ 的落点仍是一对相对顶点，则可任取另一只喜鹊 $C$，于是，$A,B,C$ 三只喜鹊飞落前后所占据的项点都构成直角三角形．若喜鹊 $A$ 和 $B$ 的落点 $A^{\prime},B^\prime$ 不是相对顶点，则可记 $A^\prime$ 的相对顶点为 $C^\prime$ 并记返回后落在 $C^\prime$ 的喜鹊是从点C飞起的．于是，$A, B,C$ 三只喜鹊飞落前后所占据的顶点都构成直角三角形．这就证明了所有不小于 $4$ 的偶数 $n$ 都满足要求．
设 $n=2 m+1, m \geqslant 3, m \in \mathbf{N}$．这时图中没有直角三角形，让我们来证明如下引理．
引理：当 $n=2 m+1, m \geqslant 3$ 时，连出所有对角线的正 $n$ 边形中，钝角三角形的个数多千所有三角形个数的一半．
引理的证明：设正 $n$ 边形为 $A_{1} A_{2} \cdots A_{n}$．这时，以对角线 $A_{1} A_{j+1}$ 为最长边的钝角三角形的个数为 $j -1$．所以钝角三角形的总数为 $S=(2 m+1)(1+2+\cdots+(m-1))=\frac{1}{2}(2 m+1) m(m-1)$ 正 $n$ 边形中三角形总数为 $t=C_{n}^{3}=\frac{1}{3}(2 m+1) m(2 m-1)$ 因为 $\begin{aligned} m-1>\frac{1}{3}(2 m-1) \Leftrightarrow & 3 m-3>2 m-1 \Leftrightarrow m>3-1=2 \end{aligned}$
后者显然成立，故知引理成立．
由引理可知，当 $n= 2m + 1,m\geqslant 3$ 时，总存在 $3$ 只喜鹊，它们飞落前后所在的 $3$ 个顶点都构成钝角三角形．这表明不小于 $7$ 的所有奇数都满足题中的要求．
综上可知，满足题中要求的所有自然数是 $n \geqslant 3, n \neq 5$
解法二
前面证明均同解法一，只是将 $n= 2m + 1,m \geqslant 3$ 的情形改证如下．
由于将正 $n$ 边形连同顶点上落的峉鹊一起旋转时，三角形的形状不变，故可假设一只喜鹊 $A$ 飞走后返回时仍然落在原处．过 $A$ 所在的顶点作正 $n$ 边形的外接圆的一条直径 $AA^\prime$，于是，这条直径两侧各有 $m$ 只喜鹊．易见，位于直径同侧的任何两只喜鹊与 $A$ 一起所在的 $3$ 个顶点都构成钝角三角形．由于 $m\geqslant 3$，所以位于直径同侧的 $m$ 只喜鹊中，飞走返回时总有两只 $B$ 和 $C$ 仍在直径的同一侧，于是，$A,B,C$ 这三只喜鹊飞落前后所在的 $3$ 个顶点都构成钝角三角形．这就证明了不小于 $7$ 的所有奇数都满足题中的要求，所以满足题中要求的所有自然数就是 $n\geqslant 3,n\ne 65$．
答案
解析
备注
