设 $ABCD$ 是一个梯形 $(AB\parallel CD)$，$E$ 是线段 $AB$ 上一点，$F$ 是线段 $CD$ 上一点，线段 $CE$ 与 $BF$ 相交于点 $H$，线段 $ED$ 与 $AF$ 相交于点 $G$．
求证：$S_{EHFG}\geqslant\dfrac{1}{4}S_{ABCD}$．
如果 $ABCD$ 是一个任意凸四边形，同样结论是否成立？请说明理由．
求证：$S_{EHFG}\geqslant\dfrac{1}{4}S_{ABCD}$．
如果 $ABCD$ 是一个任意凸四边形，同样结论是否成立？请说明理由．
【难度】
【出处】
1994第9届CMO试题
【标注】
【答案】
略
【解析】
如图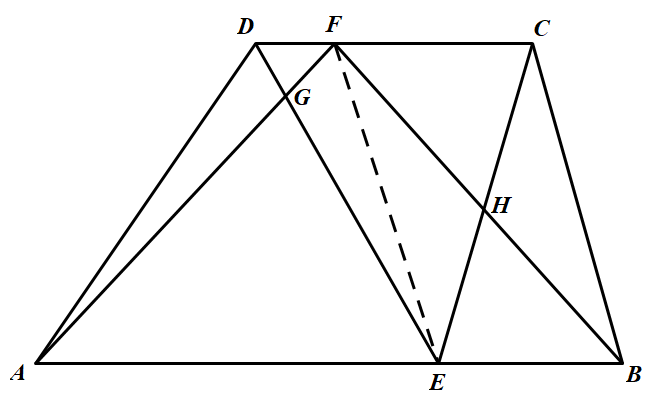
联结 $EF$．在梯形 $AEFD$ 中，显然有
$\sin \angle A G D=\sin \angle D G F=\sin \angle E G F=\sin \angle A G E$ ①
$S_{\triangle A G D}=S_{\triangle A E D}-S_{\triangle A B G}=S_{\triangle A E F}-S_{\Delta A E G}=S_{\triangle E C F}$ ②
由 ① 和 ②，有
$\left(S_{\triangle E C F}\right)^{2}= S_{\triangle E C F} \cdot S_{\triangle A C D}=\left(\dfrac{1}{2} E G \cdot G F \sin \angle E G F\right)\left(\dfrac{1}{2} A G \cdot G D \sin \angle A G D\right)\\=\left(\dfrac{1}{2} E G \cdot A G \sin \angle A G E\right)\left(\dfrac{1}{2} G F \cdot G D \sin \angle D G F\right)= S_{\triangle A C E} \cdot S_{\triangle D C F} ③ $
由 ② 和 ③ 有
$S_{A E F D}=S_{\Delta A G E}+S_{\triangle E G F}+S_{\triangle D G F}+S_{\triangle A C D}=2 S_{\triangle E G F}+\left(S_{\triangle A G E}+S_{\triangle D G F}\right) \\\geqslant 2 S_{\triangle E G F}+2 \sqrt{S_{\triangle A G E} \cdot S_{\triangle D G F}}=4 \mathrm{S}_{\triangle E G F} ④ $
类似地，有 $S_{B E F C} \geqslant 4 S_{\triangle E H F}$ ⑤
④ 加 ⑤，再乘以 $\dfrac{1}{4}$，有 $\dfrac{1}{4} S_{A B C D} \geqslant S_{E H F C}$ ⑥
对于后半题，如果 $ABCD$ 是一个任意凸四边形，结论不一定成立．举一反例如下：作一个梯形 $A B C D, B C \parallel A D, A D=1, B C=100$，梯形高 $h=100$，在 $AB$ 上取一点 $E$，作 $E F \parallel B C$，交线段 $CD$ 于点 $F$，如图所示．
已知线段 $EF$ 与 $BC$ 之间的距离为 $1$．
$S_{A B C D}=\dfrac{1}{2}(A D+B C) h=5050$ ⑦
$E F=\dfrac{1}{100}(99 B C+A D)=99.01$ ⑧
点 $G$ 到线段 $EF$ 的距离记为 $h^{\ast}$，显然
$\dfrac{h^{*}}{99-h^{*}}=\dfrac{E F}{A D}=99.01$ ⑨
从而 $h^{*}=\dfrac{99 \times 99.01}{100.01}$ ⑩
那么 $\begin{aligned} S_{E H F C}>S_{\Delta E F C}=\frac{1}{2} E F \cdot h^{*} &=\dfrac{99 \times(99.01)^{2}}{200.02}> \dfrac{1}{4} \times 5050=\dfrac{1}{4} S_{A B C D} \end{aligned}$ ⑪
联结 $EF$．在梯形 $AEFD$ 中，显然有$\sin \angle A G D=\sin \angle D G F=\sin \angle E G F=\sin \angle A G E$ ①
$S_{\triangle A G D}=S_{\triangle A E D}-S_{\triangle A B G}=S_{\triangle A E F}-S_{\Delta A E G}=S_{\triangle E C F}$ ②
由 ① 和 ②，有
$\left(S_{\triangle E C F}\right)^{2}= S_{\triangle E C F} \cdot S_{\triangle A C D}=\left(\dfrac{1}{2} E G \cdot G F \sin \angle E G F\right)\left(\dfrac{1}{2} A G \cdot G D \sin \angle A G D\right)\\=\left(\dfrac{1}{2} E G \cdot A G \sin \angle A G E\right)\left(\dfrac{1}{2} G F \cdot G D \sin \angle D G F\right)= S_{\triangle A C E} \cdot S_{\triangle D C F} ③ $
由 ② 和 ③ 有
$S_{A E F D}=S_{\Delta A G E}+S_{\triangle E G F}+S_{\triangle D G F}+S_{\triangle A C D}=2 S_{\triangle E G F}+\left(S_{\triangle A G E}+S_{\triangle D G F}\right) \\\geqslant 2 S_{\triangle E G F}+2 \sqrt{S_{\triangle A G E} \cdot S_{\triangle D G F}}=4 \mathrm{S}_{\triangle E G F} ④ $
类似地，有 $S_{B E F C} \geqslant 4 S_{\triangle E H F}$ ⑤
④ 加 ⑤，再乘以 $\dfrac{1}{4}$，有 $\dfrac{1}{4} S_{A B C D} \geqslant S_{E H F C}$ ⑥
对于后半题，如果 $ABCD$ 是一个任意凸四边形，结论不一定成立．举一反例如下：作一个梯形 $A B C D, B C \parallel A D, A D=1, B C=100$，梯形高 $h=100$，在 $AB$ 上取一点 $E$，作 $E F \parallel B C$，交线段 $CD$ 于点 $F$，如图所示．
已知线段 $EF$ 与 $BC$ 之间的距离为 $1$．$S_{A B C D}=\dfrac{1}{2}(A D+B C) h=5050$ ⑦
$E F=\dfrac{1}{100}(99 B C+A D)=99.01$ ⑧
点 $G$ 到线段 $EF$ 的距离记为 $h^{\ast}$，显然
$\dfrac{h^{*}}{99-h^{*}}=\dfrac{E F}{A D}=99.01$ ⑨
从而 $h^{*}=\dfrac{99 \times 99.01}{100.01}$ ⑩
那么 $\begin{aligned} S_{E H F C}>S_{\Delta E F C}=\frac{1}{2} E F \cdot h^{*} &=\dfrac{99 \times(99.01)^{2}}{200.02}> \dfrac{1}{4} \times 5050=\dfrac{1}{4} S_{A B C D} \end{aligned}$ ⑪
答案
解析
备注
