设 $M$ 为平面上坐标为 $(p \times 1994,7 p \times 1994)$ 的点，其中 $p$ 是素数．求满足下述条件的直角三角形的个数：
（1）三角形的三个顶点都是整点，而且 $M$ 是直角顶点；
（2）三角形的内心是坐标原．
（1）三角形的三个顶点都是整点，而且 $M$ 是直角顶点；
（2）三角形的内心是坐标原．
【难度】
【出处】
1994第9届CMO试题
【标注】
【答案】
略
【解析】
联结坐标原点 $O$ 及点 $M$，取线段 $OM$ 的中点 $l(p \times 997,7 p \times 997)$，把满足条件的一个直角三角形关于点 $l$ 作一个中心对 称，即把点 $(x,y)$ 变为点 $(p \times 1994-x, 7 p \times 1994-y)$．于是，满 足题目条件的一个整点直角三角形变为一个为之全等的整点直角三角形．三角形的内心变到点 $M$，直角顶点变到坐标原点．因此，所求整点直角三角形的个数，只须考虑直角顶点在坐标顶点，内心在点 $M$ 的情况即可．
考虑满足上述条件的整点 $\mathrm{Rt} \triangle O A B$，如图所示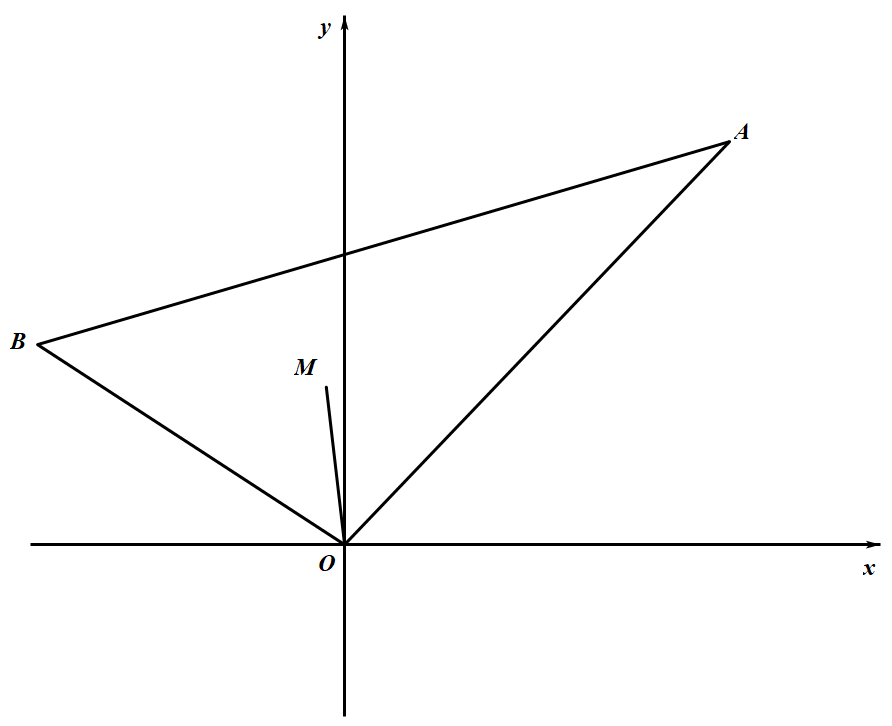
设 $\angle x O M=\beta, \angle x O A=\alpha, \alpha+\dfrac{\pi}{4}=\beta$ 由题目条件，知
$\begin{aligned} \tan \beta &=7 , \tan \alpha=\tan \left(\beta-\frac{\pi}{4}\right) =\dfrac{\tan \beta-1}{1+\tan \beta}=\dfrac{3}{4} \end{aligned}$ ①
于是，直角边 $OA$ 上的任一点的坐标可写成 $(4t,3t)$，由于 $A$ 是整点，则 $t \in \mathbf{N}, O A=5 t$．从 $\angle y O B=\alpha$，可知点 $B$ 的坐标为 $\left(-3 t^{*}, 4 t^{*}\right), t^{*} \in \mathbf{N}, O B=5 t^{*}$．直角三角形内切圆半径 $r=\dfrac{\sqrt{2}}{2} O M=5 p \times 1994$ 设 $O A=2 r+p^{*}, O B=2 r+q^{*}$ ②
由于 $OA ,OB,r$ 皆为 $5$ 的倍数，则正整数 $p^{*}, q^{*}$ 都是 $5$ 的倍数．利用圆外一点到圆的两条切线段长相等，有 $A B=\left(r+p^{*}\right)+\left(r+q^{*}\right)=2 r+p^{*}+q^{*}$ ③
由于 $\triangle OAB$ 是一个直角三角形，有
$0=A B^{2}-O A^{2}-O B^{2}=\left(2 r+p^{*}+q^{*}\right)^{2}-\left(2 r+p^{*}\right)^{2}-\left(2 r+q^{*}\right)^{2}=2 p^{*} q^{*}-4 r^{2}$ ④
于是，有 $p^{*} q^{*}=2 r^{2}$ ⑤
由于 $\dfrac{p^{*}}{5}, \dfrac{q^{*}}{5}$ 都是正整数，可得 $\dfrac{p^{*}}{5} \cdot \dfrac{q^{*}}{5}=2^{3} \times 997^{2} \times p^{2}$ ⑥
当 $p \neq 2$ 和 $p \neq 997$ 时
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j} \times p^{k}} \\ {\dfrac{q^{*}}{5}=2^{3-i} \times 997^{2-j} \times p^{2-k}}\end{array}\right.$ ⑦
这里 $i=0,1,2,3 ; j=0,1,2 ; k=0,1,2$．那么 $\left(\dfrac{p^{*}}{5}, \dfrac{q^{*}}{5}\right)$ 有 $4
\times 3\times 3=36$ 组不同的（有序）解．
当 $p=2$ 时，有
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j}} \\ {\dfrac{q^{*}}{5}=2^{5-i} \times 997^{2-j}}\end{array}\right.$ ⑧
这里 $i=0,1,2,3,4,5 ; j=0,1,2$．方程组 ⑧ 有 $6\times 3=18$ 组不同的（有序）解
当 $p=997$ 时，有
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j}} \\ {\dfrac{q^{*}}{5}=2^{3-i} \times 997^{4-j}}\end{array}\right.$ ⑨
这里 $i=0,1,2,3 ; j=0,1,2,3,4$．方程组 ⑨ 有 $4\times 5=20$ 组不同的（有序）解．
于是，所求的直角三角形个数
$S=\left\{\begin{array}{l}{36, p \neq 2 \neq 1 \mathrm{p} \neq 997} \\ {18, p=2} \\ {20, p=997}\end{array}\right.$ ⑩
考虑满足上述条件的整点 $\mathrm{Rt} \triangle O A B$，如图所示
设 $\angle x O M=\beta, \angle x O A=\alpha, \alpha+\dfrac{\pi}{4}=\beta$ 由题目条件，知$\begin{aligned} \tan \beta &=7 , \tan \alpha=\tan \left(\beta-\frac{\pi}{4}\right) =\dfrac{\tan \beta-1}{1+\tan \beta}=\dfrac{3}{4} \end{aligned}$ ①
于是，直角边 $OA$ 上的任一点的坐标可写成 $(4t,3t)$，由于 $A$ 是整点，则 $t \in \mathbf{N}, O A=5 t$．从 $\angle y O B=\alpha$，可知点 $B$ 的坐标为 $\left(-3 t^{*}, 4 t^{*}\right), t^{*} \in \mathbf{N}, O B=5 t^{*}$．直角三角形内切圆半径 $r=\dfrac{\sqrt{2}}{2} O M=5 p \times 1994$ 设 $O A=2 r+p^{*}, O B=2 r+q^{*}$ ②
由于 $OA ,OB,r$ 皆为 $5$ 的倍数，则正整数 $p^{*}, q^{*}$ 都是 $5$ 的倍数．利用圆外一点到圆的两条切线段长相等，有 $A B=\left(r+p^{*}\right)+\left(r+q^{*}\right)=2 r+p^{*}+q^{*}$ ③
由于 $\triangle OAB$ 是一个直角三角形，有
$0=A B^{2}-O A^{2}-O B^{2}=\left(2 r+p^{*}+q^{*}\right)^{2}-\left(2 r+p^{*}\right)^{2}-\left(2 r+q^{*}\right)^{2}=2 p^{*} q^{*}-4 r^{2}$ ④
于是，有 $p^{*} q^{*}=2 r^{2}$ ⑤
由于 $\dfrac{p^{*}}{5}, \dfrac{q^{*}}{5}$ 都是正整数，可得 $\dfrac{p^{*}}{5} \cdot \dfrac{q^{*}}{5}=2^{3} \times 997^{2} \times p^{2}$ ⑥
当 $p \neq 2$ 和 $p \neq 997$ 时
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j} \times p^{k}} \\ {\dfrac{q^{*}}{5}=2^{3-i} \times 997^{2-j} \times p^{2-k}}\end{array}\right.$ ⑦
这里 $i=0,1,2,3 ; j=0,1,2 ; k=0,1,2$．那么 $\left(\dfrac{p^{*}}{5}, \dfrac{q^{*}}{5}\right)$ 有 $4
\times 3\times 3=36$ 组不同的（有序）解．
当 $p=2$ 时，有
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j}} \\ {\dfrac{q^{*}}{5}=2^{5-i} \times 997^{2-j}}\end{array}\right.$ ⑧
这里 $i=0,1,2,3,4,5 ; j=0,1,2$．方程组 ⑧ 有 $6\times 3=18$ 组不同的（有序）解
当 $p=997$ 时，有
$\left\{\begin{array}{l}{\dfrac{p^{*}}{5}=2^{i} \times 997^{j}} \\ {\dfrac{q^{*}}{5}=2^{3-i} \times 997^{4-j}}\end{array}\right.$ ⑨
这里 $i=0,1,2,3 ; j=0,1,2,3,4$．方程组 ⑨ 有 $4\times 5=20$ 组不同的（有序）解．
于是，所求的直角三角形个数
$S=\left\{\begin{array}{l}{36, p \neq 2 \neq 1 \mathrm{p} \neq 997} \\ {18, p=2} \\ {20, p=997}\end{array}\right.$ ⑩
答案
解析
备注
