凸四边形 $ABCD$ 内接于圆 $O$，对角线 $AC$ 与 $BD$ 相交于 $P$．$\triangle A B P, \triangle C D P$ 的外接圆相交于 $P$ 和另一点 $Q$，且 $O,P,Q$ 三点两两不重合．试证：$\angle O Q P=90^{\circ}$．
【难度】
【出处】
1992第7届CMO试题
【标注】
【答案】
略
【解析】
证法一
如图，联结 $AO,AQ,DO,DQ$，易知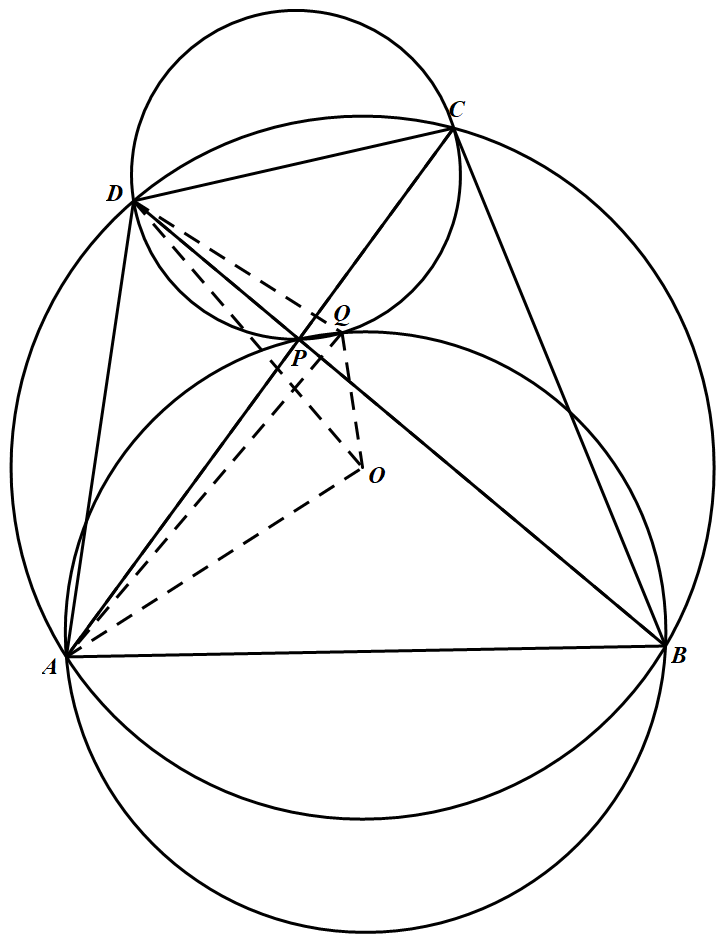
$\angle D Q A=\angle D Q P+\angle P Q A=\angle D C P+\angle A B P=2 \angle A B D$，$\angle A O D=2 \angle A B D$ 于是 $\angle D Q A=\angle A O D$ 从而，$A,O,Q,D$ 四点共圆又 $\angle A Q O=\angle A D O=90^{\circ}-\dfrac{1}{2} \angle A O D=90^{\circ}-\angle A B D$，$\angle A Q P=\angle A B D$ 所以 $\angle O Q P=\angle A Q O+\angle A Q P=90^{\circ}$
证法二
如图，$O_1,O_2$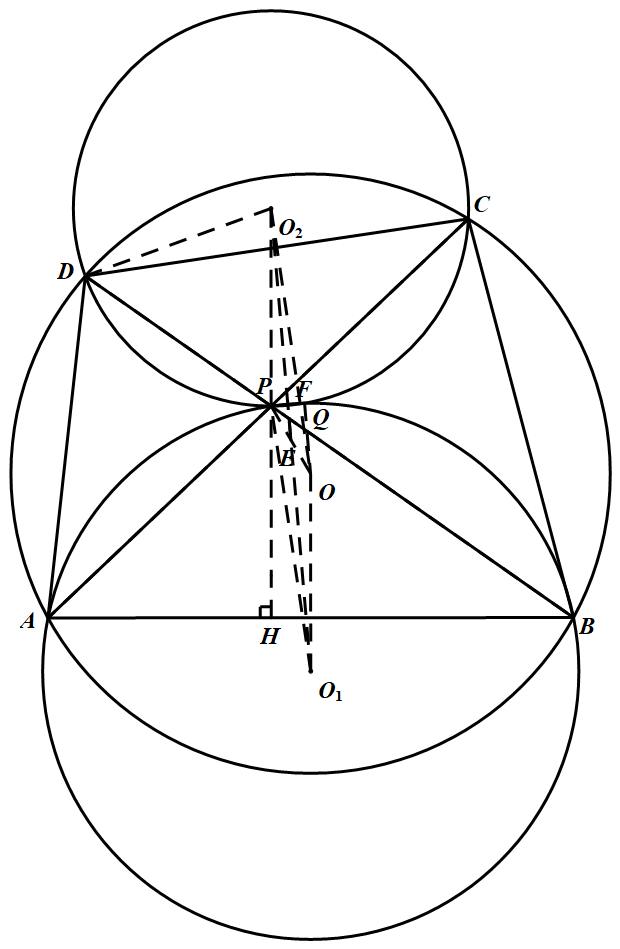
分别是 $\triangle A B P$ 和 $\triangle PCD$ 的外心．联结 $O_2P$ 并延长交 $AB$ 于 $H$．联结 $O_2D$．于是 $\begin{aligned} \angle B P H=& \angle O_{2} P D=90^{\circ}-\dfrac{1}{2} \angle D O_{2} P= 90^{\circ}-\angle D C P=90^{\circ}-\angle A B D \end{aligned}$ 从而 $\angle P H B=90^{\circ}$，即 $O_{2} P \perp A B$．又 $O O_{1} \perp A B$ 故 $O O_{1}\parallel O_2P$．
同理 $O_{2} O \parallel O_{1} P$．因而，$O_{1} O O_{2} P$ 是平行四边形，$E$ 是 $OP$ 的中点．又 $F$ 是 $PQ$ 的中点，故 $E F \parallel O Q$，即 $O_{1} O_{2} \parallel O Q$．但 $O_{2} O_{1} \bot P Q$ 故 $O Q \perp P Q$，即 $\angle O Q P=90^\circ$．
如图，联结 $AO,AQ,DO,DQ$，易知
$\angle D Q A=\angle D Q P+\angle P Q A=\angle D C P+\angle A B P=2 \angle A B D$，$\angle A O D=2 \angle A B D$ 于是 $\angle D Q A=\angle A O D$ 从而，$A,O,Q,D$ 四点共圆又 $\angle A Q O=\angle A D O=90^{\circ}-\dfrac{1}{2} \angle A O D=90^{\circ}-\angle A B D$，$\angle A Q P=\angle A B D$ 所以 $\angle O Q P=\angle A Q O+\angle A Q P=90^{\circ}$证法二
如图，$O_1,O_2$
分别是 $\triangle A B P$ 和 $\triangle PCD$ 的外心．联结 $O_2P$ 并延长交 $AB$ 于 $H$．联结 $O_2D$．于是 $\begin{aligned} \angle B P H=& \angle O_{2} P D=90^{\circ}-\dfrac{1}{2} \angle D O_{2} P= 90^{\circ}-\angle D C P=90^{\circ}-\angle A B D \end{aligned}$ 从而 $\angle P H B=90^{\circ}$，即 $O_{2} P \perp A B$．又 $O O_{1} \perp A B$ 故 $O O_{1}\parallel O_2P$．同理 $O_{2} O \parallel O_{1} P$．因而，$O_{1} O O_{2} P$ 是平行四边形，$E$ 是 $OP$ 的中点．又 $F$ 是 $PQ$ 的中点，故 $E F \parallel O Q$，即 $O_{1} O_{2} \parallel O Q$．但 $O_{2} O_{1} \bot P Q$ 故 $O Q \perp P Q$，即 $\angle O Q P=90^\circ$．
答案
解析
备注
