平面上有一个凸四边形 $A B C D$．
（1）如果平面上存在一点 $P$，使得 $\triangle A B P, \triangle B C P, \triangle C D P$ 和 $\triangle D A P$ 的面积都相等，问四边形 $ABCD$ 要满足什么条件？
（2）满足（1）的点 $P$，平面上最多有几个？证明你的结论．
（1）如果平面上存在一点 $P$，使得 $\triangle A B P, \triangle B C P, \triangle C D P$ 和 $\triangle D A P$ 的面积都相等，问四边形 $ABCD$ 要满足什么条件？
（2）满足（1）的点 $P$，平面上最多有几个？证明你的结论．
【难度】
【出处】
1991第6届CMO试题
【标注】
【答案】
略
【解析】
首先设点 $P$ 在四边形 $ABCD$ 内部，如图所示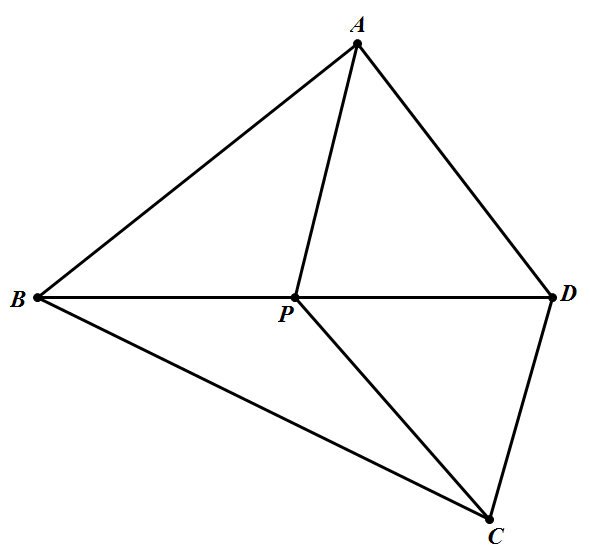
则由 $S_{\triangle A B P}=S_{\triangle C B P}$ 可知，$A,C$ 到 $BP$ 的距离相等，由 $S_{\triangle{ B AP}}=S_{\triangle D A P}$ 可知 $B,D$ 到 $AP$ 的距离相等．同理可知：$A,C$ 与 $DP$ 等距，$B,D$ 与 $CP$ 等距．于是，如果 $A, P, C$ 三点不共线，则因 $B,D$ 与 $AP,CP$ 均等距，可知必有 $A P, C P$ 过 $BD$ 的中点，因而 $P$ 就是 $BD$ 的中点，即 $B, P, D$ 三点共线，而且 $BD$ 平分对角线 $AC$．这时 $S_{\triangle AP{B}}+S _{\triangle A D P}=S_{\triangle B C P}+S_{\triangle D C P}=\dfrac{1}{2} S_{A B C D}$ 故知四边形 $A B C D$ 应满足的条件是：存在 一条对角线将它的面积平分，或者，存在一条对角线通过另一条对角线的中点．易知，此二条件是等价的而且当此条件满足时，其所述性质的点 $P$ 只能有一个，即它位于平分四边形 $ABCD$ 的面积的对角线的中点上．如果两条对角线都把四边形的面积平分，则由上述证明过程可知 $P$ 即是此二对角线的交点．
其次，设点 $P$ 在四边形 $ABCD$ 之外，如图所示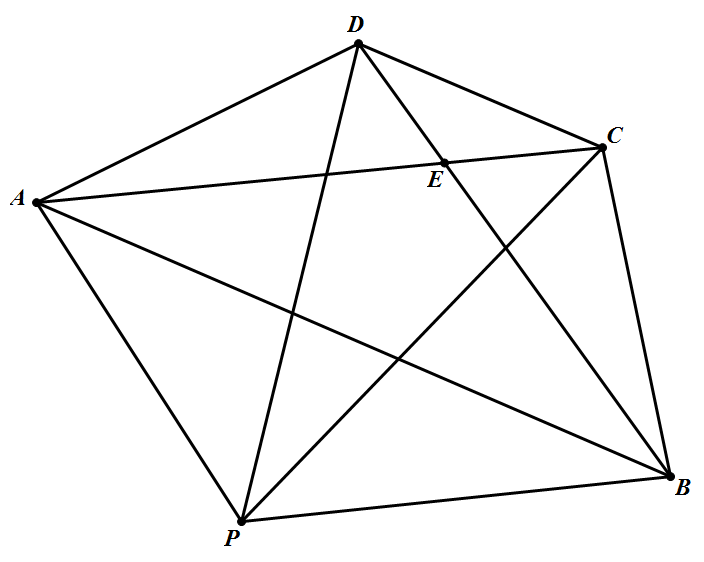
则由 $S_{\triangle A P B}=S_{\triangle C P B}$ 可知 $AC\parallel PB$，由 $S_{\Delta B P A}=S_{\triangle D {P A}}$ 可知 $B D / / P A$．记 $AC$ 与 $BD$ 的交点为 $E$，则有 $A P B E$ 是平行四边形，且 $S_{\triangle P A B}=S_{\triangle E A B}$．由于
$S_{\triangle P A B}=S_{\triangle P M D}+S_{\triangle P D C}+S_{\triangle P C B}-S_{A B C D}$ 可知 $S_{\triangle P A B}=\dfrac{1}{2} S_{A B C D}=S_{\triangle E A B}$ 由此得出四边形 $ABCD$ 具有性质：其两对角线交点与某二相邻项点所形成的三角形的面积恰是此四边形面积的一半，此即存在这样的点 $P$ 时四边形 $ABCD$ 便满足条件．此条件也是充分的即如果凸四边形 $ABCD$ 两对角线 $AC$ 与 $D$ 交于点 $E$，而且 $S_{\triangle A E B}=\dfrac{1}{2} S_{A B C D}$，则过点 $A$ 作 $\mathbf{A} P / / B C$，过点 $B$ 作 $B P / / A C$，记 $P$ 为 $AP$ 与 $BP$ 的交点，则不难验证点 $P$ 满足条件 $S_{\triangle P A B}=S_{\triangle P B C}=S_{\triangle P C D}=S_{\triangle P D A}$．
由于在四边形内、外存在所述性质的点 $P$ 时要求四边形 $ABCD$ 所满足的条件是对立的，因而，这样的点 $P$ 在平面上最多只有一个．
则由 $S_{\triangle A B P}=S_{\triangle C B P}$ 可知，$A,C$ 到 $BP$ 的距离相等，由 $S_{\triangle{ B AP}}=S_{\triangle D A P}$ 可知 $B,D$ 到 $AP$ 的距离相等．同理可知：$A,C$ 与 $DP$ 等距，$B,D$ 与 $CP$ 等距．于是，如果 $A, P, C$ 三点不共线，则因 $B,D$ 与 $AP,CP$ 均等距，可知必有 $A P, C P$ 过 $BD$ 的中点，因而 $P$ 就是 $BD$ 的中点，即 $B, P, D$ 三点共线，而且 $BD$ 平分对角线 $AC$．这时 $S_{\triangle AP{B}}+S _{\triangle A D P}=S_{\triangle B C P}+S_{\triangle D C P}=\dfrac{1}{2} S_{A B C D}$ 故知四边形 $A B C D$ 应满足的条件是：存在 一条对角线将它的面积平分，或者，存在一条对角线通过另一条对角线的中点．易知，此二条件是等价的而且当此条件满足时，其所述性质的点 $P$ 只能有一个，即它位于平分四边形 $ABCD$ 的面积的对角线的中点上．如果两条对角线都把四边形的面积平分，则由上述证明过程可知 $P$ 即是此二对角线的交点．其次，设点 $P$ 在四边形 $ABCD$ 之外，如图所示
则由 $S_{\triangle A P B}=S_{\triangle C P B}$ 可知 $AC\parallel PB$，由 $S_{\Delta B P A}=S_{\triangle D {P A}}$ 可知 $B D / / P A$．记 $AC$ 与 $BD$ 的交点为 $E$，则有 $A P B E$ 是平行四边形，且 $S_{\triangle P A B}=S_{\triangle E A B}$．由于$S_{\triangle P A B}=S_{\triangle P M D}+S_{\triangle P D C}+S_{\triangle P C B}-S_{A B C D}$ 可知 $S_{\triangle P A B}=\dfrac{1}{2} S_{A B C D}=S_{\triangle E A B}$ 由此得出四边形 $ABCD$ 具有性质：其两对角线交点与某二相邻项点所形成的三角形的面积恰是此四边形面积的一半，此即存在这样的点 $P$ 时四边形 $ABCD$ 便满足条件．此条件也是充分的即如果凸四边形 $ABCD$ 两对角线 $AC$ 与 $D$ 交于点 $E$，而且 $S_{\triangle A E B}=\dfrac{1}{2} S_{A B C D}$，则过点 $A$ 作 $\mathbf{A} P / / B C$，过点 $B$ 作 $B P / / A C$，记 $P$ 为 $AP$ 与 $BP$ 的交点，则不难验证点 $P$ 满足条件 $S_{\triangle P A B}=S_{\triangle P B C}=S_{\triangle P C D}=S_{\triangle P D A}$．
由于在四边形内、外存在所述性质的点 $P$ 时要求四边形 $ABCD$ 所满足的条件是对立的，因而，这样的点 $P$ 在平面上最多只有一个．
答案
解析
备注
