如图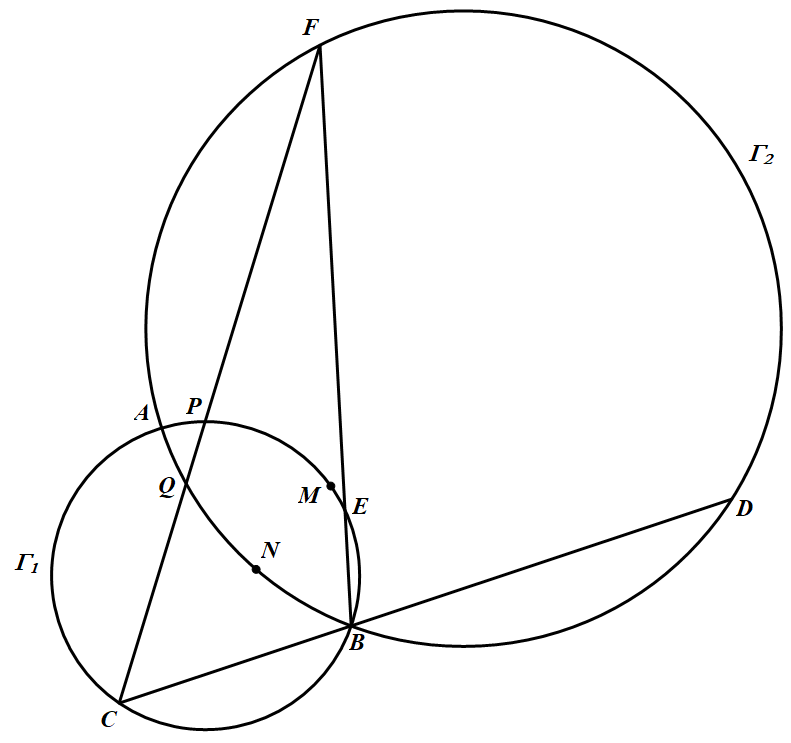
两圆 $\Gamma_{1}, \Gamma_{2}$ 交于点A、B，过点 $B$ 的一条直线分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $C、D$，过点 $B$ 的另一条直线分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $E,F$，直线 $CF$ 分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $P,Q$．设 $M,N$ 分别是 $\overparen{P B}, \overparen{Q B}$ 的中点．．若 $CD=EF$，求证：$C,F,M,N$ 四点共圆．
两圆 $\Gamma_{1}, \Gamma_{2}$ 交于点A、B，过点 $B$ 的一条直线分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $C、D$，过点 $B$ 的另一条直线分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $E,F$，直线 $CF$ 分别交圆 $\Gamma_{1}, \Gamma_{2}$ 于点 $P,Q$．设 $M,N$ 分别是 $\overparen{P B}, \overparen{Q B}$ 的中点．．若 $CD=EF$，求证：$C,F,M,N$ 四点共圆．【难度】
【出处】
2010第25届CMO试题
【标注】
【答案】
略
【解析】
联结 $AC、AD、AE、AF、DF$．
由 $\angle A D B=\angle A F B, \angle A C B=\angle A E F$ 及 $C D=E F$
$\Rightarrow \triangle A C D \cong \triangle A E F$
$\Rightarrow A D=A F$
$\Rightarrow \angle A D F=\angle A F D$
$\Rightarrow \angle A B C=\angle A F D=\angle A D F=\angle A B F$
$\Rightarrow AB$ 是 $\angle C B F$ 的角平分线．
联结 $CM、FN$．因为 $M$ 是弧 $\overparen{P B}$ 的中点，所以，$CM$ 是 $\angle D C F$ 的角平分线．
同理，$FN$ 是 $\angle CFB$ 的角平分线．
于是，$BA、CM、FN$ 三线共点．设交点为 $I$．
在圆 $\boldsymbol{\Gamma}_{1}, \boldsymbol{\Gamma}_{2}$ 中，，由圆幂定理得 $C I \cdot I M=A I \cdot I B, A I \cdot I B=N I \cdot I F\Rightarrow N I \cdot I F=C I \cdot I M .$
从而，$C、F、M、N$ 四点共圆．
由 $\angle A D B=\angle A F B, \angle A C B=\angle A E F$ 及 $C D=E F$
$\Rightarrow \triangle A C D \cong \triangle A E F$
$\Rightarrow A D=A F$
$\Rightarrow \angle A D F=\angle A F D$
$\Rightarrow \angle A B C=\angle A F D=\angle A D F=\angle A B F$
$\Rightarrow AB$ 是 $\angle C B F$ 的角平分线．
联结 $CM、FN$．因为 $M$ 是弧 $\overparen{P B}$ 的中点，所以，$CM$ 是 $\angle D C F$ 的角平分线．
同理，$FN$ 是 $\angle CFB$ 的角平分线．
于是，$BA、CM、FN$ 三线共点．设交点为 $I$．
在圆 $\boldsymbol{\Gamma}_{1}, \boldsymbol{\Gamma}_{2}$ 中，，由圆幂定理得 $C I \cdot I M=A I \cdot I B, A I \cdot I B=N I \cdot I F\Rightarrow N I \cdot I F=C I \cdot I M .$
从而，$C、F、M、N$ 四点共圆．
答案
解析
备注
