将 $m\times n$（$m,n$ 均为正整数）的方格表中每一个小方格染成白色或黑色，使得每个 $2\times 2$ 的小正方形中四个方格至多只有两个黑格．问：黑格最多有多少个？
【难度】
【出处】
2019北京大学中学生数学奖个人能力挑战赛
【标注】
【答案】
略
【解析】
若 $m,n$ 均为偶数，注意整个表格可以被分成 $\dfrac{m}{2}\times\dfrac{n}{2}$ 个 $2\times 2$ 小正方形，故黑格最多 $\dfrac{m}{2}$ 个．此时染黑第 $1,3,5,\cdots,m-1$ 行所有方格即可．
若 $m,n$ 为一奇一偶，不妨设 $m$ 为奇数且 $n$ 为偶数．去掉最后一行后整个表格可以被分成 $\dfrac{m-1}{2}\times\dfrac{n}{2}$ 个 $2\times 2$，故黑格最多 $\dfrac{mn+n}{2}$ 个．此时染黑第 $1,3,5,\cdots,m$ 行所有方格即可．
若 $m,n$ 均为奇数，不妨设 $m\leqslant n$．我们用归纳法证明黑格最多 $\dfrac{mn+n}{2}$ 个．
当 $m=1$ 时，一共只有 $n$ 个方格，全部染黑即可，结论成立．
若 $m=2k-1$ 时结论成立，则 $m=2k+1$ 时．
将这个 $m\times n$ 的表格可分为一个 $(m-2) \times(n-2)$ 的小表格，$\dfrac{m-3}{2}+\dfrac{n-3}{2}$ 个 $2\times 2$ 的小正方形和一个 $3\times 3$ 去掉右下角的形状．
在最后一个部分，若 $A,B,C,D$ 四个均为黑格，剩下的方格中只有左上角可能是黑格，此时该部分至多只有 $5$ 个黑格．
若 $A,B,C,D$ 不全为黑格，则黑格总数也不超过 $3+2=5$ 个．
故最后一个部分至多只有 $5$ 个黑格．
故黑格总数不超过 $\dfrac{(m-2)(n-2)+(n-2)}{2}+\left(\dfrac{m-3}{2}+\dfrac{n-3}{2}\right)$．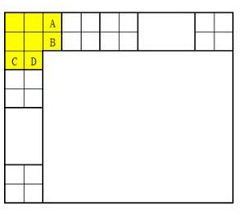
此时染黑第 $1,3,5,\cdots,m$ 行所有方格即可．
综上即可得证．
若 $m,n$ 为一奇一偶，不妨设 $m$ 为奇数且 $n$ 为偶数．去掉最后一行后整个表格可以被分成 $\dfrac{m-1}{2}\times\dfrac{n}{2}$ 个 $2\times 2$，故黑格最多 $\dfrac{mn+n}{2}$ 个．此时染黑第 $1,3,5,\cdots,m$ 行所有方格即可．
若 $m,n$ 均为奇数，不妨设 $m\leqslant n$．我们用归纳法证明黑格最多 $\dfrac{mn+n}{2}$ 个．
当 $m=1$ 时，一共只有 $n$ 个方格，全部染黑即可，结论成立．
若 $m=2k-1$ 时结论成立，则 $m=2k+1$ 时．
将这个 $m\times n$ 的表格可分为一个 $(m-2) \times(n-2)$ 的小表格，$\dfrac{m-3}{2}+\dfrac{n-3}{2}$ 个 $2\times 2$ 的小正方形和一个 $3\times 3$ 去掉右下角的形状．
在最后一个部分，若 $A,B,C,D$ 四个均为黑格，剩下的方格中只有左上角可能是黑格，此时该部分至多只有 $5$ 个黑格．
若 $A,B,C,D$ 不全为黑格，则黑格总数也不超过 $3+2=5$ 个．
故最后一个部分至多只有 $5$ 个黑格．
故黑格总数不超过 $\dfrac{(m-2)(n-2)+(n-2)}{2}+\left(\dfrac{m-3}{2}+\dfrac{n-3}{2}\right)$．
此时染黑第 $1,3,5,\cdots,m$ 行所有方格即可．综上即可得证．
答案
解析
备注
