如图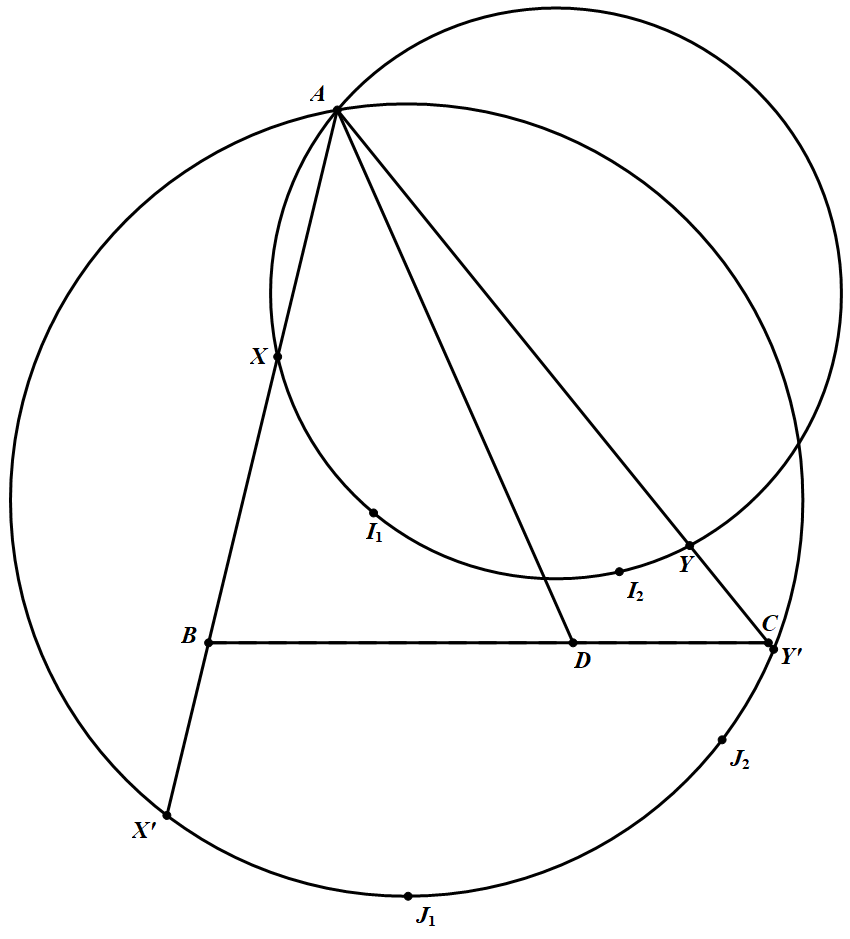
在 $\triangle ABC$ 中，已知点 $D$ 为 $BC$ 边上一点．$I_{1}, I_{2}$ 分别为 $\triangle A B D, \triangle A D C$ 的内心，$J_{1}, J_{2}$ 分别为 $\triangle A B D, \triangle A D C$ 的点 $A$ 所对旁心．$\triangle AI_1I_2$ 的外接圆分别交 $AB,AC$ 于点 $X,Y$，$\triangle AJ_1J_2$ 的外接圆分别交 $AB,AC$ 延长线于点 $X^{\prime} , Y^{\prime}$．
求证：$B X-B X^{\prime}=C Y-C Y^{\prime}$．
在 $\triangle ABC$ 中，已知点 $D$ 为 $BC$ 边上一点．$I_{1}, I_{2}$ 分别为 $\triangle A B D, \triangle A D C$ 的内心，$J_{1}, J_{2}$ 分别为 $\triangle A B D, \triangle A D C$ 的点 $A$ 所对旁心．$\triangle AI_1I_2$ 的外接圆分别交 $AB,AC$ 于点 $X,Y$，$\triangle AJ_1J_2$ 的外接圆分别交 $AB,AC$ 延长线于点 $X^{\prime} , Y^{\prime}$．求证：$B X-B X^{\prime}=C Y-C Y^{\prime}$．
【难度】
【出处】
2019年爱尖子数学能力测评
【标注】
【答案】
略
【解析】
略
答案
解析
备注
