如图
在圆内接 $\triangle ABC$ 中，$\angle A$ 为最大角，不含点 $A$ 的 弧 $\overparen{BC}$ 上两点 $D、E$ 分别为弧 $\overparen{ABC},\overparen{ACB}$ 的中点记过点 $A、B$ 且与 $AC$ 相切的圆为 $\odot O_1$，，过点 $A、E$ 且与 $AD$ 相切的圆为 $\odot O_2$，$\odot O_1$ 与 $\odot O_2$ 交于点 $A、P$．证明：$ AP$ 平分 $\angle BAC$．
在圆内接 $\triangle ABC$ 中，$\angle A$ 为最大角，不含点 $A$ 的 弧 $\overparen{BC}$ 上两点 $D、E$ 分别为弧 $\overparen{ABC},\overparen{ACB}$ 的中点记过点 $A、B$ 且与 $AC$ 相切的圆为 $\odot O_1$，，过点 $A、E$ 且与 $AD$ 相切的圆为 $\odot O_2$，$\odot O_1$ 与 $\odot O_2$ 交于点 $A、P$．证明：$ AP$ 平分 $\angle BAC$．【难度】
【出处】
2012第27届CMO试题
【标注】
【答案】
略
【解析】
如图，联结 $EP、AE、BE、BP、CD$．
分别记 $\angle B A C, \angle A B C, \angle A C B$ 为 $\angle A, \angle B, \angle C$，$X,Y$ 分别为 $CA$ 延长线，$DA$ 延长线上的任意一点．
由已知条件易得 $AD =DC,AE =EB$．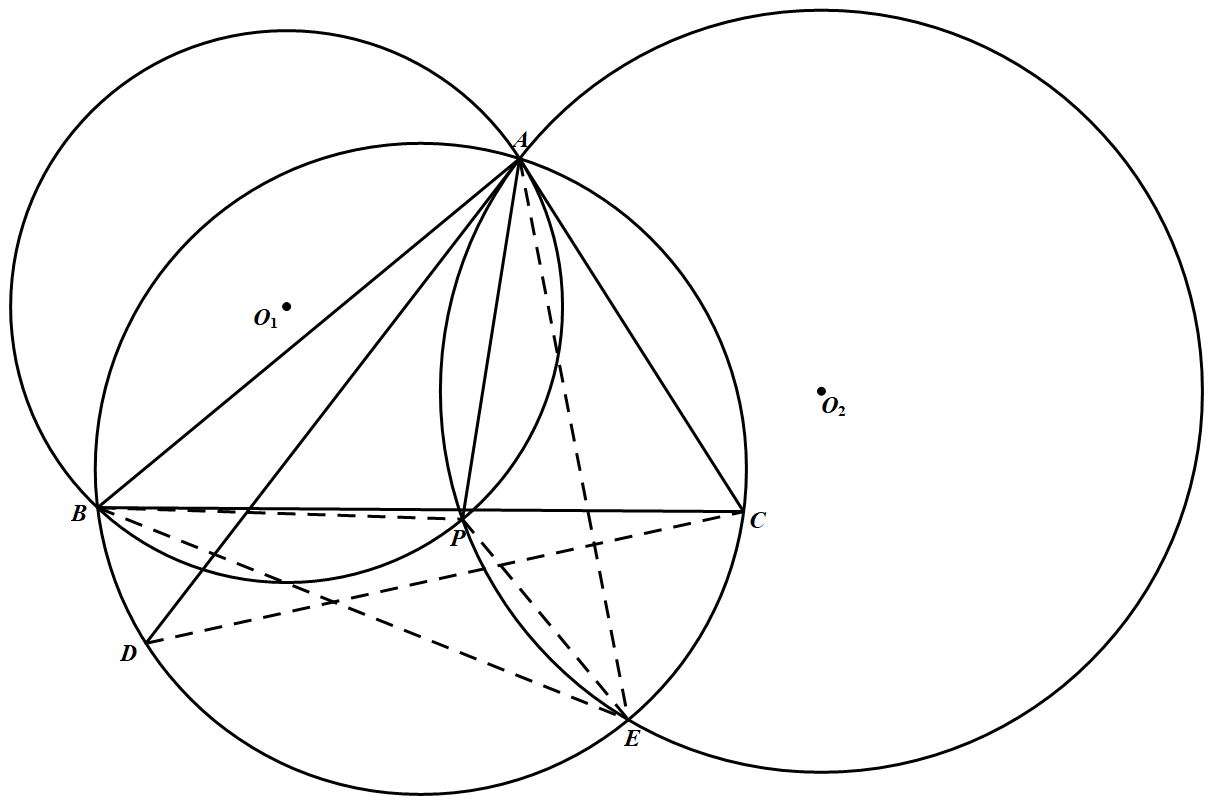
结合 $A、B、D、E、C$ 五点共圆得 $\angle B A E=90^{\circ}-\dfrac{1}{2} \angle A E B=90^{\circ}-\dfrac{\angle C}{2},\angle C A D=90^{\circ}-\dfrac{1}{2} \angle A D C=90^{\circ}-\dfrac{\angle B}{2}$
由 $AC、AD$ 分别切 $\odot O_1 ,\odot O_2$ 于点 $A$ 得
$\angle A P B=\angle B A X=180^{\circ}-\angle A,\angle A B P=\angle C A P$
及 $\angle A P E=\angle E A Y=180^{\circ}-\angle D A E$
$=180^{\circ}-(\angle B A E+\angle C A D-\angle A)$
$=180^{\circ}-\left(90^{\circ}-\dfrac{\angle C}{2}\right)-\left(90^{\circ}-\dfrac{\angle B}{2}\right)+\angle A$
$=90^{\circ}+\dfrac{\angle A}{2}$
故 $\angle B P E=360^{\circ}-\angle A P B-\angle A P E=90^{\circ}+\dfrac{\angle A}{2}=\angle A P E$
在 $\triangle APE$ 与 $\triangle BPE$ 中，分别运用正弦定
理并结合 $AE=BE$，得 $\dfrac{\sin \angle P A E}{\sin \angle A P E}=\dfrac{P E}{A E}=\dfrac{P E}{B E}=\dfrac{\sin \angle P B E}{\sin \angle B P E}$
故 $\sin \angle P A E=\sin \angle P B E$
又因为 $\angle APE,\angle BPE$ 均为钝角，所以，$\angle PAE,\angle PBE$ 均为锐角．
于是，$\angle P A E=\angle P B E$．
故 $\angle B A P=\angle B A E-\angle P A E=\angle A B E-\angle P B E=\angle A B P=\angle C A P$．
分别记 $\angle B A C, \angle A B C, \angle A C B$ 为 $\angle A, \angle B, \angle C$，$X,Y$ 分别为 $CA$ 延长线，$DA$ 延长线上的任意一点．
由已知条件易得 $AD =DC,AE =EB$．
结合 $A、B、D、E、C$ 五点共圆得 $\angle B A E=90^{\circ}-\dfrac{1}{2} \angle A E B=90^{\circ}-\dfrac{\angle C}{2},\angle C A D=90^{\circ}-\dfrac{1}{2} \angle A D C=90^{\circ}-\dfrac{\angle B}{2}$由 $AC、AD$ 分别切 $\odot O_1 ,\odot O_2$ 于点 $A$ 得
$\angle A P B=\angle B A X=180^{\circ}-\angle A,\angle A B P=\angle C A P$
及 $\angle A P E=\angle E A Y=180^{\circ}-\angle D A E$
$=180^{\circ}-(\angle B A E+\angle C A D-\angle A)$
$=180^{\circ}-\left(90^{\circ}-\dfrac{\angle C}{2}\right)-\left(90^{\circ}-\dfrac{\angle B}{2}\right)+\angle A$
$=90^{\circ}+\dfrac{\angle A}{2}$
故 $\angle B P E=360^{\circ}-\angle A P B-\angle A P E=90^{\circ}+\dfrac{\angle A}{2}=\angle A P E$
在 $\triangle APE$ 与 $\triangle BPE$ 中，分别运用正弦定
理并结合 $AE=BE$，得 $\dfrac{\sin \angle P A E}{\sin \angle A P E}=\dfrac{P E}{A E}=\dfrac{P E}{B E}=\dfrac{\sin \angle P B E}{\sin \angle B P E}$
故 $\sin \angle P A E=\sin \angle P B E$
又因为 $\angle APE,\angle BPE$ 均为钝角，所以，$\angle PAE,\angle PBE$ 均为锐角．
于是，$\angle P A E=\angle P B E$．
故 $\angle B A P=\angle B A E-\angle P A E=\angle A B E-\angle P B E=\angle A B P=\angle C A P$．
答案
解析
备注
