如图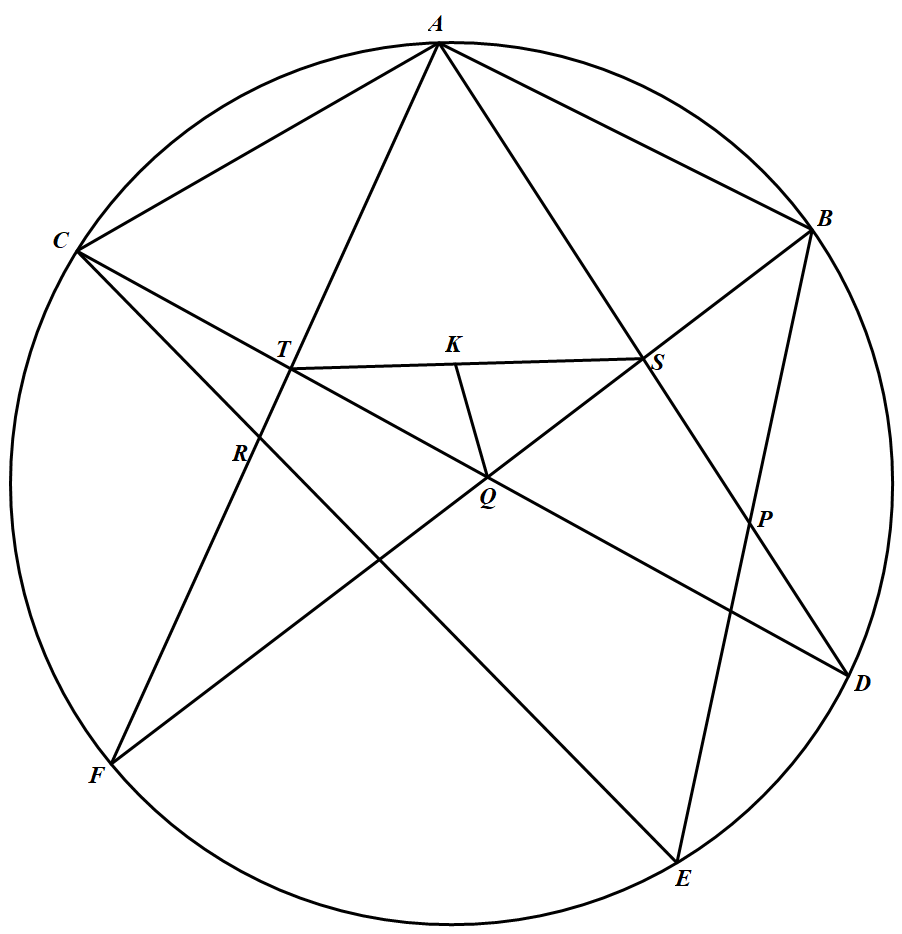
设 $A、B、D、E、F、C$ 依次为一个圆上的六个点，满足 $AB=AC$．直线 $AD$ 与 $BE$ 交于点 $P$，直线 $AF$ 与 $CE$ 交于点 $R$，直线 $BF$ 与 $CD$ 交于点 $Q$，直线 $AD$ 与 $BF$ 交于点 $S$，直线 $AF$ 与 $CD$ 交于点 $T$．点 $K$ 在线段 $ST$ 上，使得 $\angle S K Q=\angle A C E$．证明：$\dfrac{S K}{K T}=\dfrac{P Q}{Q R}$．
设 $A、B、D、E、F、C$ 依次为一个圆上的六个点，满足 $AB=AC$．直线 $AD$ 与 $BE$ 交于点 $P$，直线 $AF$ 与 $CE$ 交于点 $R$，直线 $BF$ 与 $CD$ 交于点 $Q$，直线 $AD$ 与 $BF$ 交于点 $S$，直线 $AF$ 与 $CD$ 交于点 $T$．点 $K$ 在线段 $ST$ 上，使得 $\angle S K Q=\angle A C E$．证明：$\dfrac{S K}{K T}=\dfrac{P Q}{Q R}$．【难度】
【出处】
2014第30届CMO试题
【标注】
【答案】
略
【解析】
如图，联结 $BC、RP、DF$．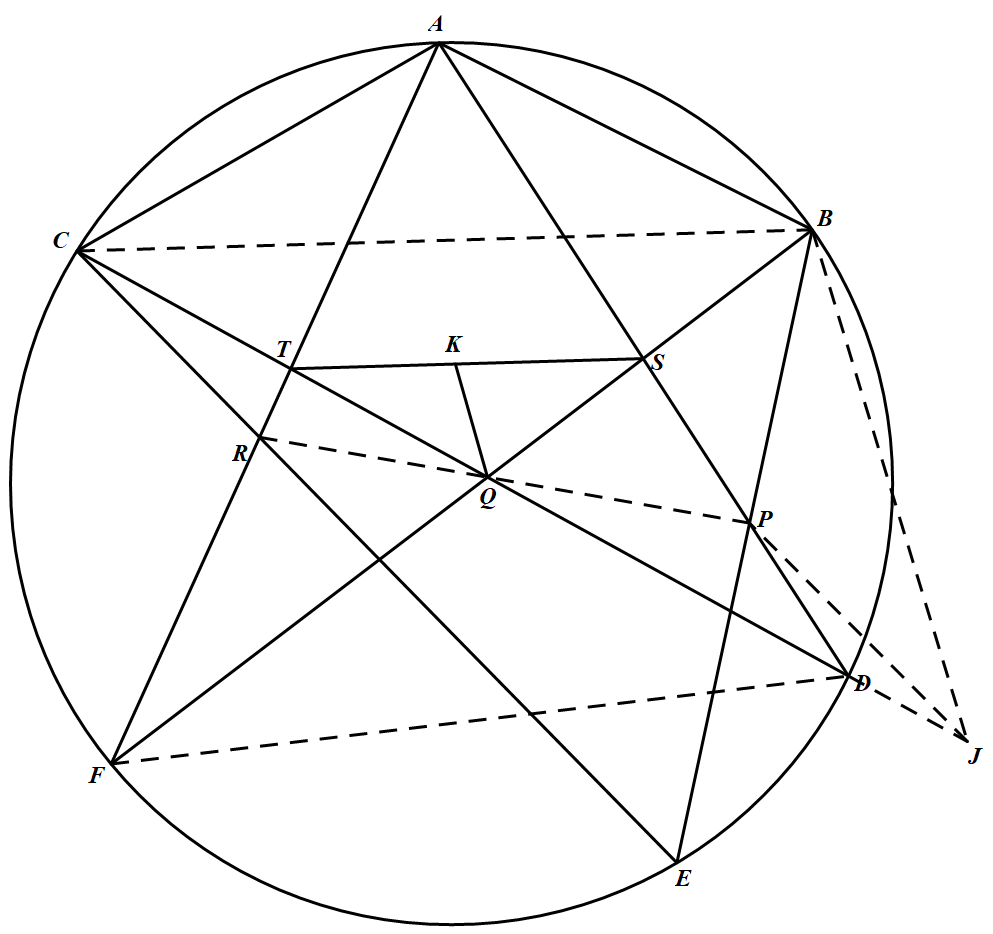
由 $AB=AC$，知 $\angle A D C=\angle A F B$．所以，$S、D、F、T$ 四点共圆．
于是，$\angle Q S K=\angle T D F=\angle R A C$．
结合 $\angle S K Q=\angle A C E$，得 $\triangle Q S K \sim \triangle R A C$．
类似地，$\triangle Q T K \sim \triangle P A B$．
从而，$\dfrac{S K}{K Q}=\dfrac{A C}{C R}, \dfrac{K Q}{K T}=\dfrac{B P}{B A}$．
故 $\dfrac{S K}{K T}=\dfrac{S K}{K Q} \cdot \dfrac{K Q}{K T}=\dfrac{A C}{C R} \cdot \dfrac{B P}{B A}=\dfrac{B P}{C R}$ ①
由帕斯卡定理知 $P、Q、R$ 三点共线．
设点 $J$ 在射线 $CD$ 上，使 $\triangle B C J \sim \triangle B A P$，联结 $PJ$．
由 $\dfrac{B P}{B J}=\dfrac{A B}{C B}$，及 $\angle A B C=\angle P B A-\angle P B C=\angle J B C-\angle P B C=\angle J B P$ 得 $\triangle B P J \sim\triangle B A C$．
结合 $AB=AC$，知 $PB=PJ$．
又 $\angle D P E=\angle B P A=\angle B J C$，则 $B, J, D,P$ 四点共圆．
故 $\angle P J Q=\angle D B E=\angle D C E$．
从而，$P J \parallel C R$．
于是，$\dfrac{B P}{C R}=\dfrac{P J}{C R}=\dfrac{P Q}{Q R}$．②
由式 ①、② 知命题成立．
由 $AB=AC$，知 $\angle A D C=\angle A F B$．所以，$S、D、F、T$ 四点共圆．于是，$\angle Q S K=\angle T D F=\angle R A C$．
结合 $\angle S K Q=\angle A C E$，得 $\triangle Q S K \sim \triangle R A C$．
类似地，$\triangle Q T K \sim \triangle P A B$．
从而，$\dfrac{S K}{K Q}=\dfrac{A C}{C R}, \dfrac{K Q}{K T}=\dfrac{B P}{B A}$．
故 $\dfrac{S K}{K T}=\dfrac{S K}{K Q} \cdot \dfrac{K Q}{K T}=\dfrac{A C}{C R} \cdot \dfrac{B P}{B A}=\dfrac{B P}{C R}$ ①
由帕斯卡定理知 $P、Q、R$ 三点共线．
设点 $J$ 在射线 $CD$ 上，使 $\triangle B C J \sim \triangle B A P$，联结 $PJ$．
由 $\dfrac{B P}{B J}=\dfrac{A B}{C B}$，及 $\angle A B C=\angle P B A-\angle P B C=\angle J B C-\angle P B C=\angle J B P$ 得 $\triangle B P J \sim\triangle B A C$．
结合 $AB=AC$，知 $PB=PJ$．
又 $\angle D P E=\angle B P A=\angle B J C$，则 $B, J, D,P$ 四点共圆．
故 $\angle P J Q=\angle D B E=\angle D C E$．
从而，$P J \parallel C R$．
于是，$\dfrac{B P}{C R}=\dfrac{P J}{C R}=\dfrac{P Q}{Q R}$．②
由式 ①、② 知命题成立．
答案
解析
备注
