如图
在凸四边形 $ABCD$ 中，$K、L、M、N$ 分别为边 $AB、BC、CD、DA$ 上的点，满足 $\dfrac{A K}{K B}=\dfrac{D A}{B C}, \dfrac{B L}{L C}=\dfrac{A B}{C D}, \dfrac{C M}{M D}=\dfrac{B C}{D A}, \dfrac{D N}{N A}=\dfrac{C D}{A B}$．
延长 $AB、DC$ 交于点 $E$，延长 $AD、BC$ 交于点 $F$．设 $\triangle AEF$ 的内切圆在边 $AE、AF$ 上的切点分别为 $S,T$，$\triangle CEF$ 的内切圆在边 $CE、CF$ 上的切点分别为 $U,V$，证明：若 $K、L、M、N$ 四点共圆，则 $S、T、U、V$ 四点共圆．
在凸四边形 $ABCD$ 中，$K、L、M、N$ 分别为边 $AB、BC、CD、DA$ 上的点，满足 $\dfrac{A K}{K B}=\dfrac{D A}{B C}, \dfrac{B L}{L C}=\dfrac{A B}{C D}, \dfrac{C M}{M D}=\dfrac{B C}{D A}, \dfrac{D N}{N A}=\dfrac{C D}{A B}$．延长 $AB、DC$ 交于点 $E$，延长 $AD、BC$ 交于点 $F$．设 $\triangle AEF$ 的内切圆在边 $AE、AF$ 上的切点分别为 $S,T$，$\triangle CEF$ 的内切圆在边 $CE、CF$ 上的切点分别为 $U,V$，证明：若 $K、L、M、N$ 四点共圆，则 $S、T、U、V$ 四点共圆．
【难度】
【出处】
2015第31届CMO试题
【标注】
【答案】
略
【解析】
设 $AB=a ,BC=b,CD=c,DA=d$．
由已知得
$A K=\dfrac{a d}{b+d}, B K=\dfrac{a b}{b+d}, B L=\dfrac{a b}{a+c}$
$C L=\dfrac{b c}{a+c}, C M=\dfrac{b c}{b+d}, D M=\dfrac{c d}{b+d}$
$D N=\dfrac{c d}{a+c}, A N=\dfrac{a d}{a+c}$
若 $a+c>b+d$，则 $A K>A N \Rightarrow \angle A K N<\angle K N A$．
类似地，$\angle B K L<\angle K L B,\angle C M L<\angle M L C, \angle D M N<\angle M N D$
由此推出
$2 \pi-\angle A K N-\angle B K L-\angle C M L-\angle D M N>2 \pi-\angle K N A-\angle K I B-\angle M N C-\angle M N D\Rightarrow \angle N M L+\angle N K L>\angle M N K+\angle M L K$
这与 $K, L, M, N$ 四点共圆矛盾．
故 $ a+c>b+d$ 不成立．
类似地，$a+c<b+d$ 也不成立．
因而，$ a+c=b+d$，故四边形 $ABCD$ 有内切圆 $\Gamma$
如图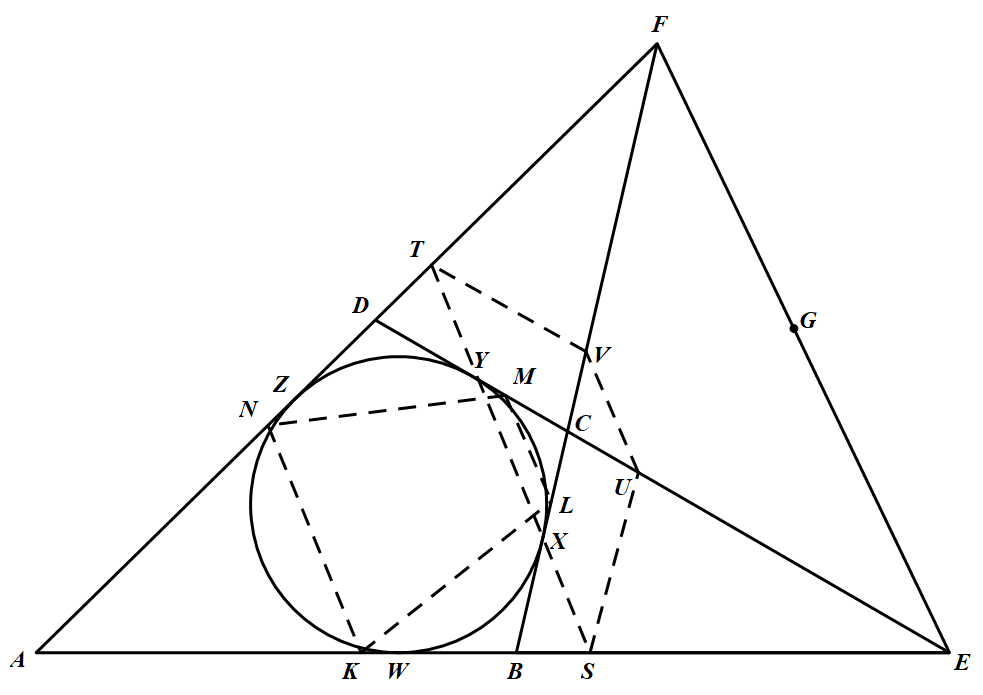
设圆 $Gamma$ 与边 $AB、BC、CD、DA$ 分别切于点 $W,X,Y,Z$．则 $A E-A F=W E-Z F=E Y-F X=E C-C F$．
设 $\triangle AEF$ 的内切圆、$\triangle CEF$ 的内切圆在边 $EF$ 上的切点分别为 $G、H$ 则
$2(F G-F H)=(E F+A F-A E)-(E F+C F-C E)=(A F-A E)-(C F-C E)=0$
因此，$\triangle AEF$ 的内切圆、$\triangle CEF$ 的内切圆与边 $EF$ 切于同一点，仍记为 $G$．
由 $ES=EG=EU$ 及 $FT=FG=FV$，知
$\angle E U S=\dfrac{\pi-\angle U E S}{2}=\dfrac{\angle A+\angle A D C}{2},\angle F T V=\dfrac{\pi-\angle T F V}{2}=\dfrac{\angle A+\angle A B C}{2}$．
而 $\angle A T S=\dfrac{\pi-\angle A}{2}, \angle C U V=\dfrac{\pi-\angle B C D}{2}$，
故
$\angle V T S+\angle V U S=(\pi-\angle F T V-\angle A T S)+(\angle C U V+\pi-\angle E U S) \\=\left(\pi-\dfrac{\angle A+\angle A B C}{2}-\dfrac{\pi-\angle A}{2}\right)+\left(\dfrac{\pi-\angle B C D}{2}+\pi-\dfrac{\angle A+\angle A D C}{2}\right) = \pi $
从而，$S、T、V、U$ 四点共圆．
由已知得
$A K=\dfrac{a d}{b+d}, B K=\dfrac{a b}{b+d}, B L=\dfrac{a b}{a+c}$
$C L=\dfrac{b c}{a+c}, C M=\dfrac{b c}{b+d}, D M=\dfrac{c d}{b+d}$
$D N=\dfrac{c d}{a+c}, A N=\dfrac{a d}{a+c}$
若 $a+c>b+d$，则 $A K>A N \Rightarrow \angle A K N<\angle K N A$．
类似地，$\angle B K L<\angle K L B,\angle C M L<\angle M L C, \angle D M N<\angle M N D$
由此推出
$2 \pi-\angle A K N-\angle B K L-\angle C M L-\angle D M N>2 \pi-\angle K N A-\angle K I B-\angle M N C-\angle M N D\Rightarrow \angle N M L+\angle N K L>\angle M N K+\angle M L K$
这与 $K, L, M, N$ 四点共圆矛盾．
故 $ a+c>b+d$ 不成立．
类似地，$a+c<b+d$ 也不成立．
因而，$ a+c=b+d$，故四边形 $ABCD$ 有内切圆 $\Gamma$
如图
设圆 $Gamma$ 与边 $AB、BC、CD、DA$ 分别切于点 $W,X,Y,Z$．则 $A E-A F=W E-Z F=E Y-F X=E C-C F$．设 $\triangle AEF$ 的内切圆、$\triangle CEF$ 的内切圆在边 $EF$ 上的切点分别为 $G、H$ 则
$2(F G-F H)=(E F+A F-A E)-(E F+C F-C E)=(A F-A E)-(C F-C E)=0$
因此，$\triangle AEF$ 的内切圆、$\triangle CEF$ 的内切圆与边 $EF$ 切于同一点，仍记为 $G$．
由 $ES=EG=EU$ 及 $FT=FG=FV$，知
$\angle E U S=\dfrac{\pi-\angle U E S}{2}=\dfrac{\angle A+\angle A D C}{2},\angle F T V=\dfrac{\pi-\angle T F V}{2}=\dfrac{\angle A+\angle A B C}{2}$．
而 $\angle A T S=\dfrac{\pi-\angle A}{2}, \angle C U V=\dfrac{\pi-\angle B C D}{2}$，
故
$\angle V T S+\angle V U S=(\pi-\angle F T V-\angle A T S)+(\angle C U V+\pi-\angle E U S) \\=\left(\pi-\dfrac{\angle A+\angle A B C}{2}-\dfrac{\pi-\angle A}{2}\right)+\left(\dfrac{\pi-\angle B C D}{2}+\pi-\dfrac{\angle A+\angle A D C}{2}\right) = \pi $
从而，$S、T、V、U$ 四点共圆．
答案
解析
备注
