在平面中，对任意给定的凸四边形 $ABCD$，证明：存在正方形 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$（其顶点可以按顺时针或逆时针标记），使得点 $A^\prime$ 与 $A$、点 $B^\prime$ 与 $B$、点 $C^\prime$ 与 $C$、点 $D^\prime$ 与 $D$ 分别不重合，且直线 $AA^\prime、BB^\prime、CC^\prime、DD^\prime$ 经过同一个点．
【难度】
【出处】
2015第31届CMO试题
【标注】
【答案】
略
【解析】
当四边形 $ABCD$ 为矩形时，在 $\angle BAD$ 的平分线上取一点 $A^\prime$，使得 $A^\prime$ 在射线 $AB、AD$ 上的投影分别为 $B^\prime、D^\prime$，满足点 $B^\prime$ 与 $B$、点 $D^\prime$ 与 $D$ 分别不重合．再令点 $C^\prime$ 与 $A$ 重合此时，四边形 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ 为正方形，且 $AA^\prime、BB^\prime、CC^\prime、DD^\prime$ 经过点 $A$．如图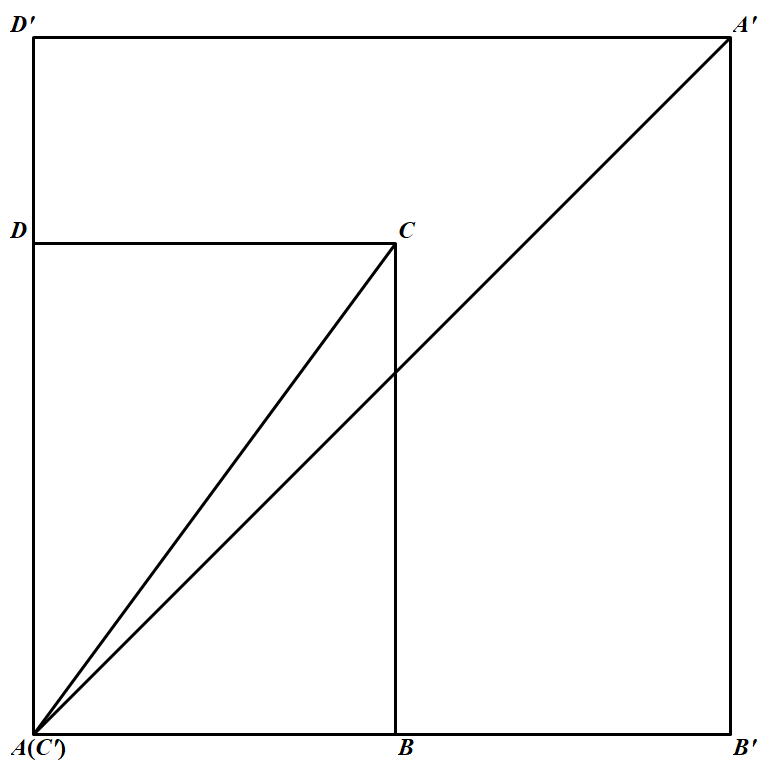
当四边形 $ABCD$ 不为矩形时，四个内角中必有锐角，不妨
设 $\angle BAD$ 为锐角，点 $C$ 在 $\angle BAD$ 内．
如图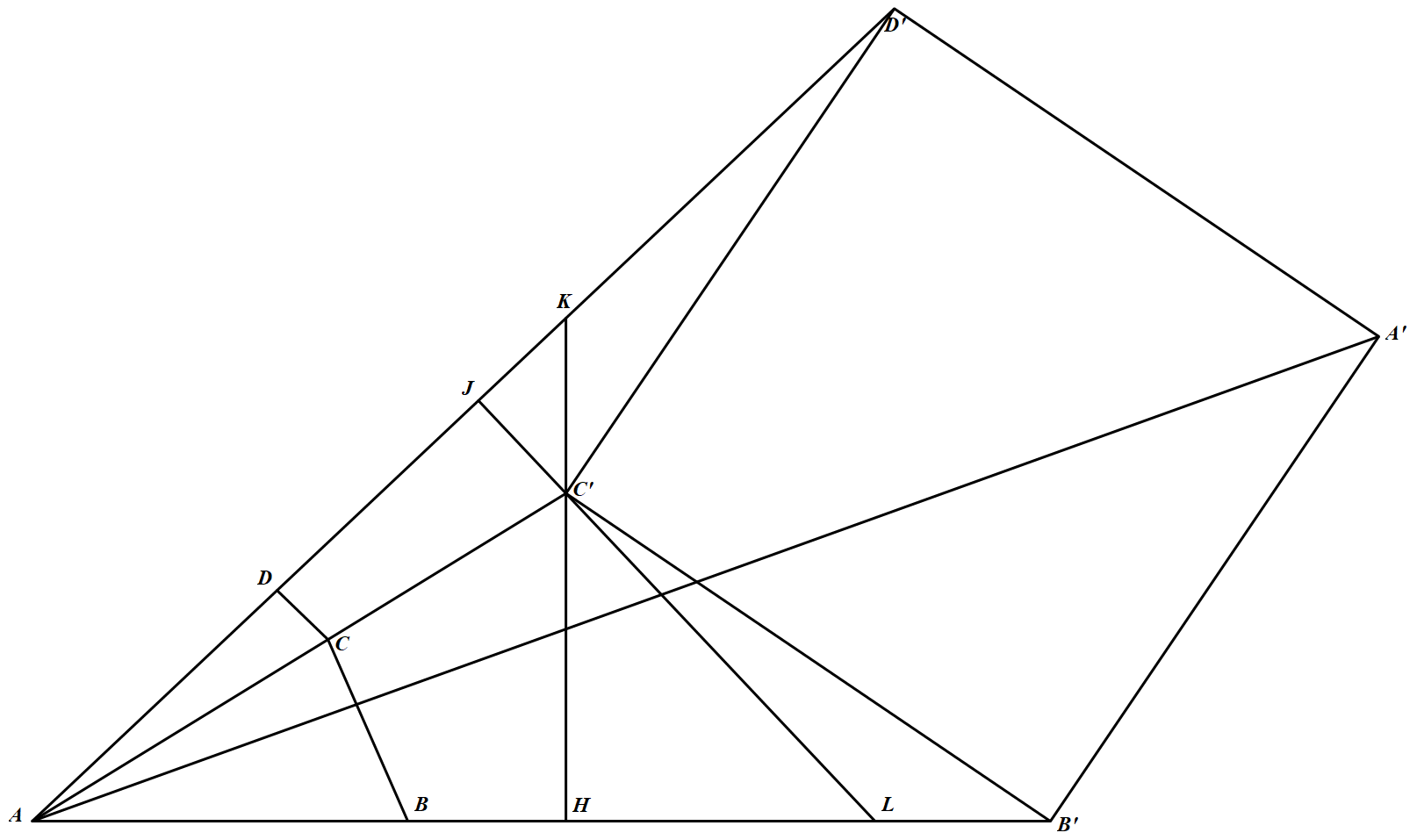
在 $AC$ 延长线上取一点 $C^\prime$，使得 $C^\prime$ 在 $AB、AD$ 上的投影 $H,J$，分别在 $AB、AD$ 的延长线上．设 $HC^\prime$ 与 $AJ$ 的延长线交于点 $K$，$JC^\prime$ 与 $AH$ 的延长线交于点 $L$．分别延长 $AL,AK$ 至点 $B^\prime,D^\prime$，使得 $L B^{\prime}=K C^{\prime}, K D^{\prime}=L C^{\prime}$．
又注意到，$\angle B^{\prime} L C^{\prime}=90^{\circ}+\angle L A K=\angle C^{\prime} K D^{\prime}$，则
$\triangle B^{\prime} L C^{\prime} \cong \triangle C^{\prime} K D^{\prime}\Rightarrow B^{\prime} C^{\prime}=C^{\prime} D^{\prime}, \angle B^{\prime} C^{\prime} D^{\prime}=180^{\circ}-\angle K C^{\prime} D^{\prime}-\angle B^{\prime} C^{\prime} H=180^{\circ}-\angle L B^{\prime} C^{\prime}-\left(90^{\circ}-\angle L B^{\prime} C^{\prime}\right)=90^{\circ}$
于是，存在以 $B^\prime、C^\prime、D^\prime$ 为三个顶点的正方形 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$，其中，点 $A^\prime$ 在 $\angle B^{\prime} C^{\prime} D^{\prime}$ 内．
故点 $A^\prime$ 与 $A$ 不重合．此时，直线 $AA^\prime、BB^\prime、CC^\prime、DD^\prime$ 经过点 $A$．
当四边形 $ABCD$ 不为矩形时，四个内角中必有锐角，不妨设 $\angle BAD$ 为锐角，点 $C$ 在 $\angle BAD$ 内．
如图
在 $AC$ 延长线上取一点 $C^\prime$，使得 $C^\prime$ 在 $AB、AD$ 上的投影 $H,J$，分别在 $AB、AD$ 的延长线上．设 $HC^\prime$ 与 $AJ$ 的延长线交于点 $K$，$JC^\prime$ 与 $AH$ 的延长线交于点 $L$．分别延长 $AL,AK$ 至点 $B^\prime,D^\prime$，使得 $L B^{\prime}=K C^{\prime}, K D^{\prime}=L C^{\prime}$．又注意到，$\angle B^{\prime} L C^{\prime}=90^{\circ}+\angle L A K=\angle C^{\prime} K D^{\prime}$，则
$\triangle B^{\prime} L C^{\prime} \cong \triangle C^{\prime} K D^{\prime}\Rightarrow B^{\prime} C^{\prime}=C^{\prime} D^{\prime}, \angle B^{\prime} C^{\prime} D^{\prime}=180^{\circ}-\angle K C^{\prime} D^{\prime}-\angle B^{\prime} C^{\prime} H=180^{\circ}-\angle L B^{\prime} C^{\prime}-\left(90^{\circ}-\angle L B^{\prime} C^{\prime}\right)=90^{\circ}$
于是，存在以 $B^\prime、C^\prime、D^\prime$ 为三个顶点的正方形 $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$，其中，点 $A^\prime$ 在 $\angle B^{\prime} C^{\prime} D^{\prime}$ 内．
故点 $A^\prime$ 与 $A$ 不重合．此时，直线 $AA^\prime、BB^\prime、CC^\prime、DD^\prime$ 经过点 $A$．
答案
解析
备注
