如图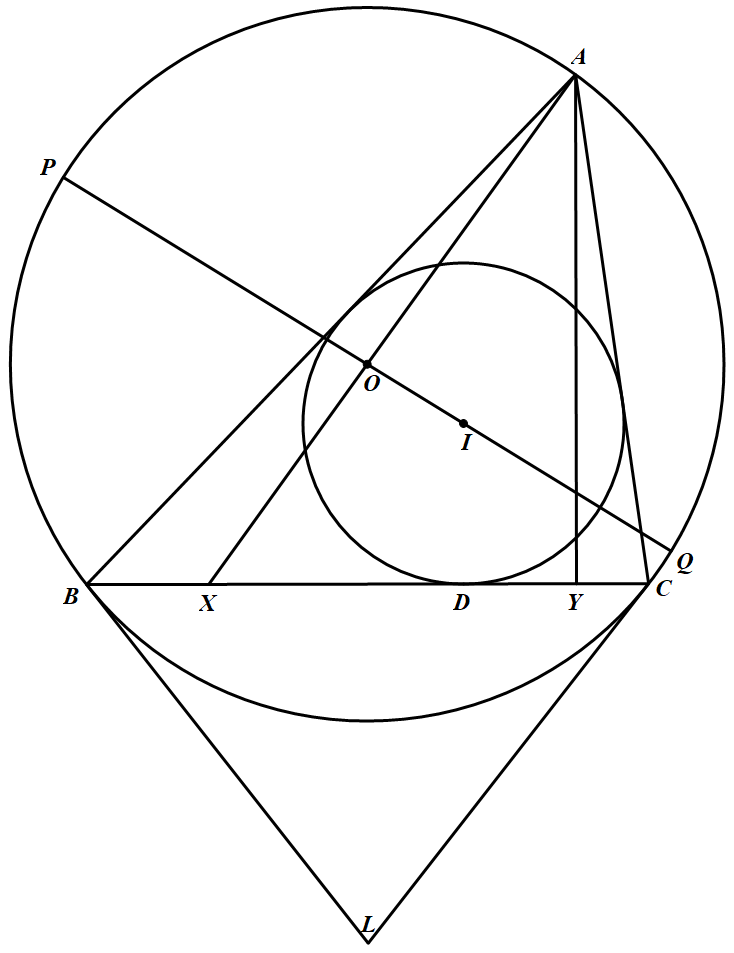
在锐角 $\triangle ABC$ 中，$AB>AC$，$\odot O,\odot I$ 分别为 $\triangle ABC$ 的外接圆、内切圆，$\odot I$，与边 $BC$ 切于点 $D$，直线 $AO$ 与边 $BC$ 交于点 $X$，$AY$ 为边 $BC$ 上的高，$\odot O$ 在点 $B,C$ 处的切线交于点 $l$，$PQ$ 为过点 $I$ 的 $\odot O$ 直径．证明：$A、D、L$ 三点共线当且仅当 $P、X、Y、Q$ 四点共圆．
在锐角 $\triangle ABC$ 中，$AB>AC$，$\odot O,\odot I$ 分别为 $\triangle ABC$ 的外接圆、内切圆，$\odot I$，与边 $BC$ 切于点 $D$，直线 $AO$ 与边 $BC$ 交于点 $X$，$AY$ 为边 $BC$ 上的高，$\odot O$ 在点 $B,C$ 处的切线交于点 $l$，$PQ$ 为过点 $I$ 的 $\odot O$ 直径．证明：$A、D、L$ 三点共线当且仅当 $P、X、Y、Q$ 四点共圆．【难度】
【出处】
2016第32届CMO试题
【标注】
【答案】
略
【解析】
如图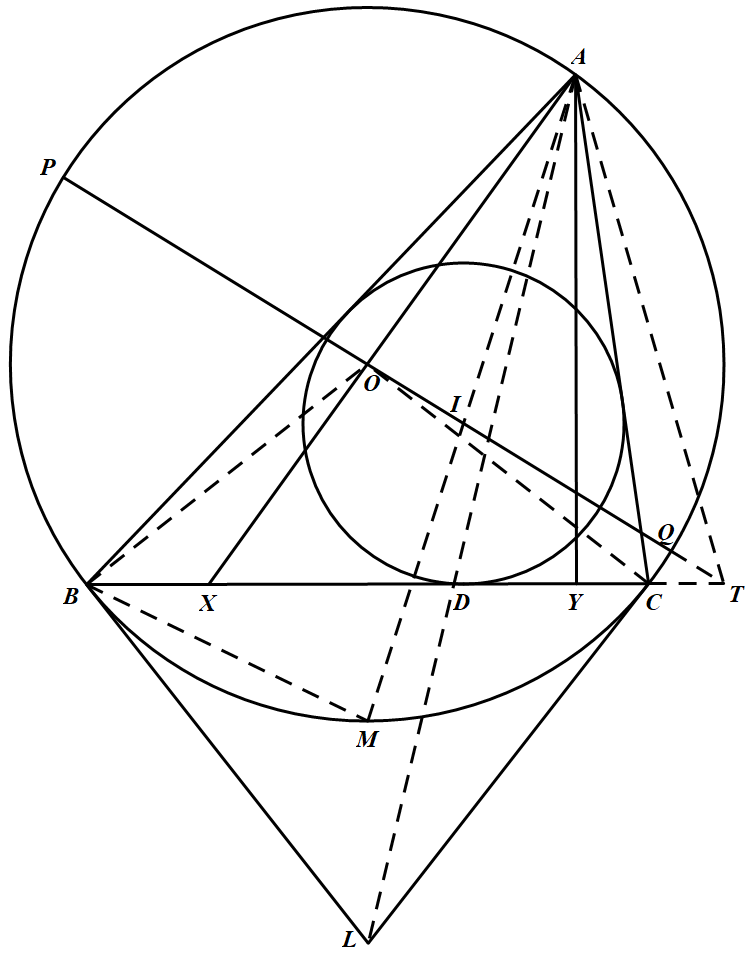
记 $a=B C, b=C A, c=A B, p=\dfrac{1}{2}(a+b+c)$ 为 $\triangle ABC$ 的半周长．
于是，$B D=p-b, C D=p-c$．
首先，$A, D, L $ 三点共线 $\Leftrightarrow \dfrac{S_{\triangle A B L}}{S_{\triangle A C L}}=\dfrac{B D}{C D}$．
注意到，
$\dfrac{B D}{C D}=\dfrac{p-b}{p-c}=\dfrac{a-b+c}{a+b-c}$
$\dfrac{S_{\triangle A B L}}{S_{\triangle A C L}}=\dfrac{\dfrac{1}{2} A B \cdot B L \sin \angle A B L}{\dfrac{1}{2} A C \cdot C L \sin \angle A C L}$
$=\dfrac{c}{b} \cdot \dfrac{\sin \angle A B L}{\sin \angle A C L}=\dfrac{c}{b} \cdot \dfrac{\sin \angle A C B}{\sin \angle A B C}=\dfrac{c^{2}}{b^{2}}$
只要证 $\dfrac{c^{2}}{b^{2}}=\dfrac{a-b+c}{a+b-c}$．
再由 $b<c$，化简得 $b^{2}+c^{2}=a(b+c)$．
故 $A, D, L$ 三点共线 $\Leftrightarrow b^{2}+c^{2}=a(b+c)$．
过点 $A$ 作 $\odot O$ 的切线，与 $BC$ 的延长线交于点 $T$．延长 $AI$ 与 $BC$ 交于点 $F$．
下面证明：$O, I, T$ 三点共线 $\Leftrightarrow b^{2}+c^{2}=a(b+c)$．
由梅涅劳斯定理知 $O,I,T$ 三点共线 $\Leftrightarrow \dfrac{A O}{O X} \cdot \dfrac{X T}{T F} \cdot \dfrac{F I}{I A}=1$ ①
记 $\angle A T X=\theta, \angle B A C=\alpha,\angle A B C=\beta, \angle A C B=\gamma$．
则 $\theta=\angle A C B-\angle C A T=\gamma-\beta$．
由面积比与面积正弦定理知
$\dfrac{A O}{O X}=\dfrac{S_{\triangle A O B}+S_{\triangle A O C}}{S_{\triangle B O C}}=\dfrac{\sin 2 \beta+\sin 2 \gamma}{\sin 2 \alpha}=\dfrac{2 \sin (\beta+\gamma) \cdot \cos (\beta-\gamma)}{2 \sin \alpha \cdot \cos \alpha}=\dfrac{\cos \theta}{\cos \alpha}$
取弧 $\overparen{BC}$ 的中点 $M$，由 $\triangle A F C \sim \triangle A B M$ 结合弦切角定理有 $\angle T A F=\angle A B M=\angle A F C \Rightarrow T F=T A$．
故 $\dfrac{X T}{T F}=\dfrac{X T}{T A}=\dfrac{1}{\cos \theta}$．
由角平分线定理及比例性质得 $\dfrac{F I}{I A}=\dfrac{B F}{c}=\dfrac{C F}{b}=\dfrac{B F+C F}{b+c}=\dfrac{a}{b+c}$．
于是，式 ① 左边为 $\dfrac{A O}{O X} \cdot \dfrac{X T}{T F} \cdot \dfrac{F I}{I A}=\dfrac{\cos \theta}{\cos \alpha} \cdot \dfrac{1}{\cos \theta} \cdot \dfrac{a}{b+c}=\dfrac{1}{\cos \alpha} \cdot \dfrac{a}{b+c}=\dfrac{2 a b c}{(b+c)\left(b^{2}+c^{2}-a^{2}\right)}$
由 $(b+c)\left(b^{2}+c^{2}-a^{2}\right)-2 a b c=(a+b+c)\left(b^{2}+c^{2}-a(b+c)\right)$
知式 ① 成立等价于 $b^{2}+c^{2}=a(b+c)$．
所以，$A、D、L$ 三点共线当且仅当 $O,I,T$ 三点共线．
当 $O、I、T$ 三点共线时，点 $T$ 也在直线 $PQ$ 上．
由圆幂定理以及 $Rt\triangle XAT$ 中的射影定理有 $T Q \cdot T P=T A^{2}=T Y \cdot T X$．
故 $P、X、Y、Q$ 四点共圆．
反之，若 $P ,X,Y,Q$ 四点共圆，考虑 $\triangle ABC$ 的外接圆 $\Gamma_1$，点 $P、X、Y、Q$ 所在圆周 $\Gamma_2$ 以及 $\triangle AXY$ 的外接圆 $\Gamma_3$．
由 $\angle B A X=\dfrac{\pi}{2}-\gamma=\angle C A Y\Rightarrow \angle T A Y=\angle T A C+\angle C A Y=\beta+\angle B A X=\angle A X C$
从而，$TA$ 也为圆 $\Gamma_3$ 的切线，圆 $\Gamma_1$ 与 $\Gamma_3$ 切于点 $A$．
注意到，圆 $\Gamma_1$ 与 $\Gamma_3$，圆 $\Gamma_1$ 与圆 $\Gamma_2$，
圆 $\Gamma_2$ 与圆 $\Gamma_3$ 的根轴分别为直线 $AT、PQ、XY$．
由蒙日定理，知 $AT、PQ、XY$ 三线共点，即 $O,I,T$ 三点共线．
从而，$A、D、L$ 三点共线当且仅当 $O,I,T$ 三点共线，当且仅当 $P、X、Y、Q$ 四点共圆．
记 $a=B C, b=C A, c=A B, p=\dfrac{1}{2}(a+b+c)$ 为 $\triangle ABC$ 的半周长．于是，$B D=p-b, C D=p-c$．
首先，$A, D, L $ 三点共线 $\Leftrightarrow \dfrac{S_{\triangle A B L}}{S_{\triangle A C L}}=\dfrac{B D}{C D}$．
注意到，
$\dfrac{B D}{C D}=\dfrac{p-b}{p-c}=\dfrac{a-b+c}{a+b-c}$
$\dfrac{S_{\triangle A B L}}{S_{\triangle A C L}}=\dfrac{\dfrac{1}{2} A B \cdot B L \sin \angle A B L}{\dfrac{1}{2} A C \cdot C L \sin \angle A C L}$
$=\dfrac{c}{b} \cdot \dfrac{\sin \angle A B L}{\sin \angle A C L}=\dfrac{c}{b} \cdot \dfrac{\sin \angle A C B}{\sin \angle A B C}=\dfrac{c^{2}}{b^{2}}$
只要证 $\dfrac{c^{2}}{b^{2}}=\dfrac{a-b+c}{a+b-c}$．
再由 $b<c$，化简得 $b^{2}+c^{2}=a(b+c)$．
故 $A, D, L$ 三点共线 $\Leftrightarrow b^{2}+c^{2}=a(b+c)$．
过点 $A$ 作 $\odot O$ 的切线，与 $BC$ 的延长线交于点 $T$．延长 $AI$ 与 $BC$ 交于点 $F$．
下面证明：$O, I, T$ 三点共线 $\Leftrightarrow b^{2}+c^{2}=a(b+c)$．
由梅涅劳斯定理知 $O,I,T$ 三点共线 $\Leftrightarrow \dfrac{A O}{O X} \cdot \dfrac{X T}{T F} \cdot \dfrac{F I}{I A}=1$ ①
记 $\angle A T X=\theta, \angle B A C=\alpha,\angle A B C=\beta, \angle A C B=\gamma$．
则 $\theta=\angle A C B-\angle C A T=\gamma-\beta$．
由面积比与面积正弦定理知
$\dfrac{A O}{O X}=\dfrac{S_{\triangle A O B}+S_{\triangle A O C}}{S_{\triangle B O C}}=\dfrac{\sin 2 \beta+\sin 2 \gamma}{\sin 2 \alpha}=\dfrac{2 \sin (\beta+\gamma) \cdot \cos (\beta-\gamma)}{2 \sin \alpha \cdot \cos \alpha}=\dfrac{\cos \theta}{\cos \alpha}$
取弧 $\overparen{BC}$ 的中点 $M$，由 $\triangle A F C \sim \triangle A B M$ 结合弦切角定理有 $\angle T A F=\angle A B M=\angle A F C \Rightarrow T F=T A$．
故 $\dfrac{X T}{T F}=\dfrac{X T}{T A}=\dfrac{1}{\cos \theta}$．
由角平分线定理及比例性质得 $\dfrac{F I}{I A}=\dfrac{B F}{c}=\dfrac{C F}{b}=\dfrac{B F+C F}{b+c}=\dfrac{a}{b+c}$．
于是，式 ① 左边为 $\dfrac{A O}{O X} \cdot \dfrac{X T}{T F} \cdot \dfrac{F I}{I A}=\dfrac{\cos \theta}{\cos \alpha} \cdot \dfrac{1}{\cos \theta} \cdot \dfrac{a}{b+c}=\dfrac{1}{\cos \alpha} \cdot \dfrac{a}{b+c}=\dfrac{2 a b c}{(b+c)\left(b^{2}+c^{2}-a^{2}\right)}$
由 $(b+c)\left(b^{2}+c^{2}-a^{2}\right)-2 a b c=(a+b+c)\left(b^{2}+c^{2}-a(b+c)\right)$
知式 ① 成立等价于 $b^{2}+c^{2}=a(b+c)$．
所以，$A、D、L$ 三点共线当且仅当 $O,I,T$ 三点共线．
当 $O、I、T$ 三点共线时，点 $T$ 也在直线 $PQ$ 上．
由圆幂定理以及 $Rt\triangle XAT$ 中的射影定理有 $T Q \cdot T P=T A^{2}=T Y \cdot T X$．
故 $P、X、Y、Q$ 四点共圆．
反之，若 $P ,X,Y,Q$ 四点共圆，考虑 $\triangle ABC$ 的外接圆 $\Gamma_1$，点 $P、X、Y、Q$ 所在圆周 $\Gamma_2$ 以及 $\triangle AXY$ 的外接圆 $\Gamma_3$．
由 $\angle B A X=\dfrac{\pi}{2}-\gamma=\angle C A Y\Rightarrow \angle T A Y=\angle T A C+\angle C A Y=\beta+\angle B A X=\angle A X C$
从而，$TA$ 也为圆 $\Gamma_3$ 的切线，圆 $\Gamma_1$ 与 $\Gamma_3$ 切于点 $A$．
注意到，圆 $\Gamma_1$ 与 $\Gamma_3$，圆 $\Gamma_1$ 与圆 $\Gamma_2$，
圆 $\Gamma_2$ 与圆 $\Gamma_3$ 的根轴分别为直线 $AT、PQ、XY$．
由蒙日定理，知 $AT、PQ、XY$ 三线共点，即 $O,I,T$ 三点共线．
从而，$A、D、L$ 三点共线当且仅当 $O,I,T$ 三点共线，当且仅当 $P、X、Y、Q$ 四点共圆．
答案
解析
备注
