矩形 $R$ 被分割成 $2 016$ 个小矩形,每个小矩形的边均平行于矩形 $R$ 的边,小矩形的顶点称为“结点”.一条在小矩形边上的线段,若其两个端点均为结点,且其内部不含其他结点,则称这条线段为“基本线段”.考虑所有分割方式,求基本线段条数的最大值和最小值.
如图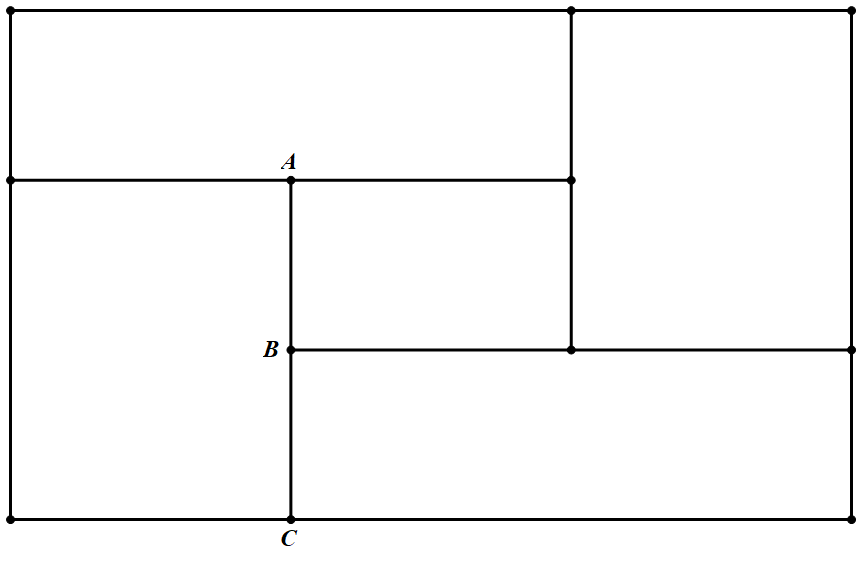 矩形 $R$ 被分割成五个小矩形,共有 $16$ 条基本线段.线段 $AB、BC$ 为基本线段,线段 $AC$ 不为基本线段.
矩形 $R$ 被分割成五个小矩形,共有 $16$ 条基本线段.线段 $AB、BC$ 为基本线段,线段 $AC$ 不为基本线段.
如图
 矩形 $R$ 被分割成五个小矩形,共有 $16$ 条基本线段.线段 $AB、BC$ 为基本线段,线段 $AC$ 不为基本线段.
矩形 $R$ 被分割成五个小矩形,共有 $16$ 条基本线段.线段 $AB、BC$ 为基本线段,线段 $AC$ 不为基本线段.【难度】
【出处】
2016第32届CMO试题
【标注】
【答案】
略
【解析】
以所有结点为顶点、基本线段为边作图 $G$.设基本线段共有 $N$ 条,$N$ 即为图 $G$ 的边数.易知,图 $G$ 的顶点的度只能为 $2、3$ 或 $4$.
度为 $2$ 的顶点恰有四个,即矩形 $R$ 的四个顶点.
设度为 $3、4$ 的顶点分别有 $x,y$ 个.由图的边数与顶点度数的关系有
$N=\dfrac{1}{2}(4 \times 2+3 x+4 y)=4+\dfrac{3}{2} x+2 y$ ①
又每个小矩形有四个顶点,按重复计算,共有 $2 016\times 4$ 个顶点,度为 $2$ 的顶点恰为一个小矩形的顶点,被计算 $1$ 次,度为 $3$ 的顶点恰为两个小矩形的顶点,被计算 $2$ 次,度为 $4$ 的顶点恰为四个小矩形的顶点,被计算 $4$ 次.
故 $2016 \times 4=4+2 x+4 y\Rightarrow x+2 y=4030$ ②
将式 ② 代人式 ① 得 $N=4034+\dfrac{1}{2} x$ ③
由式 ③,知求 $N$ 的最大值和最小值等价于求 $x$ 的最大值和最小值,并由式 ②,知也等价于求 $y$ 的最小值和最大值.
考虑将矩形 $R$ 用 $2 015$ 条垂直线段分割成 $2 016$ 个小矩形,此时没有度为 $4$ 的顶点,$y$ 取得最小值 $0$,$x$ 取得最大值 $4 030$.
因此,$N_{\max }=6049$.
下面求 $N$ 的最小值.
设在矩形 $R$ 的内部的所有基本线段落在 $s$ 条水平直线和 $t$ 条垂直直线上.则矩形 $R$ 至多被分成 $(s+1)(t+1)$ 个小矩形.
故 $(s+1)(t+1) \geqslant 2016$.
设在一条垂直直线 $l$ 上有一条基本线段 $e$,将 $e$ 向两端延长至两个结点直至无法延长(再延长就进人其他小矩形内部或走出矩形 $R$),这样得到的两个结点均为图 $G$ 中度数为 $3$ 的顶点,形如“$\top$”和“$bot$”,这样,$l$ 对应了至少两个度为 $3$ 的顶点.类似地,每条含有矩形 $R$ 内部基本线段的水平直线也对应了至少两个度为 $3$ 的顶点,形如“$\vdash$”和“$\dashv$”,这些度为 $3$ 的顶点互不相同.
故 $x \geqslant 2 s+2 t$ ④
由 $ s+t=(s+1)+(t+1)-2$
$\geqslant 2 \sqrt{(s+1)(t+1)}-2$
$\geqslant 2 \sqrt{2016}-2>87$
$\Rightarrow s+t \geqslant 88$
代入式 ④ 得 $x\geqslant 176$
再代入式 ③ 有 $N \geqslant 4122$.
考虑用 $44$ 条水平直线和 $44$ 条垂直直线先将矩形 $R$ 分成 $45^2=2 025$ 个小矩形,再将第一行中任意十个连续的小矩形合并为一个小矩形,此时,矩形 $R$ 被分割成 $2 016$ 个小矩形,且度为 $3$ 的顶点恰有 $176$ 个,$N$ 取到最小值 $N_{\min }=4122$.
度为 $2$ 的顶点恰有四个,即矩形 $R$ 的四个顶点.
设度为 $3、4$ 的顶点分别有 $x,y$ 个.由图的边数与顶点度数的关系有
$N=\dfrac{1}{2}(4 \times 2+3 x+4 y)=4+\dfrac{3}{2} x+2 y$ ①
又每个小矩形有四个顶点,按重复计算,共有 $2 016\times 4$ 个顶点,度为 $2$ 的顶点恰为一个小矩形的顶点,被计算 $1$ 次,度为 $3$ 的顶点恰为两个小矩形的顶点,被计算 $2$ 次,度为 $4$ 的顶点恰为四个小矩形的顶点,被计算 $4$ 次.
故 $2016 \times 4=4+2 x+4 y\Rightarrow x+2 y=4030$ ②
将式 ② 代人式 ① 得 $N=4034+\dfrac{1}{2} x$ ③
由式 ③,知求 $N$ 的最大值和最小值等价于求 $x$ 的最大值和最小值,并由式 ②,知也等价于求 $y$ 的最小值和最大值.
考虑将矩形 $R$ 用 $2 015$ 条垂直线段分割成 $2 016$ 个小矩形,此时没有度为 $4$ 的顶点,$y$ 取得最小值 $0$,$x$ 取得最大值 $4 030$.
因此,$N_{\max }=6049$.
下面求 $N$ 的最小值.
设在矩形 $R$ 的内部的所有基本线段落在 $s$ 条水平直线和 $t$ 条垂直直线上.则矩形 $R$ 至多被分成 $(s+1)(t+1)$ 个小矩形.
故 $(s+1)(t+1) \geqslant 2016$.
设在一条垂直直线 $l$ 上有一条基本线段 $e$,将 $e$ 向两端延长至两个结点直至无法延长(再延长就进人其他小矩形内部或走出矩形 $R$),这样得到的两个结点均为图 $G$ 中度数为 $3$ 的顶点,形如“$\top$”和“$bot$”,这样,$l$ 对应了至少两个度为 $3$ 的顶点.类似地,每条含有矩形 $R$ 内部基本线段的水平直线也对应了至少两个度为 $3$ 的顶点,形如“$\vdash$”和“$\dashv$”,这些度为 $3$ 的顶点互不相同.
故 $x \geqslant 2 s+2 t$ ④
由 $ s+t=(s+1)+(t+1)-2$
$\geqslant 2 \sqrt{(s+1)(t+1)}-2$
$\geqslant 2 \sqrt{2016}-2>87$
$\Rightarrow s+t \geqslant 88$
代入式 ④ 得 $x\geqslant 176$
再代入式 ③ 有 $N \geqslant 4122$.
考虑用 $44$ 条水平直线和 $44$ 条垂直直线先将矩形 $R$ 分成 $45^2=2 025$ 个小矩形,再将第一行中任意十个连续的小矩形合并为一个小矩形,此时,矩形 $R$ 被分割成 $2 016$ 个小矩形,且度为 $3$ 的顶点恰有 $176$ 个,$N$ 取到最小值 $N_{\min }=4122$.
答案
解析
备注