如图，圆内接四边形 $ABCD$ 的对角线交于点 $P$，$\triangle APD$ 的外接圆、$\triangle BPC$ 的外接圆分别与线段 $AB$ 交于另一点 $E、F,I、J$ 分别为 $\triangle ADE、\triangle BCF$ 的内心，线段 $IJ$ 与 $AC$ 交于点 $K$．证明：$A、I、K,E$ 四点共圆．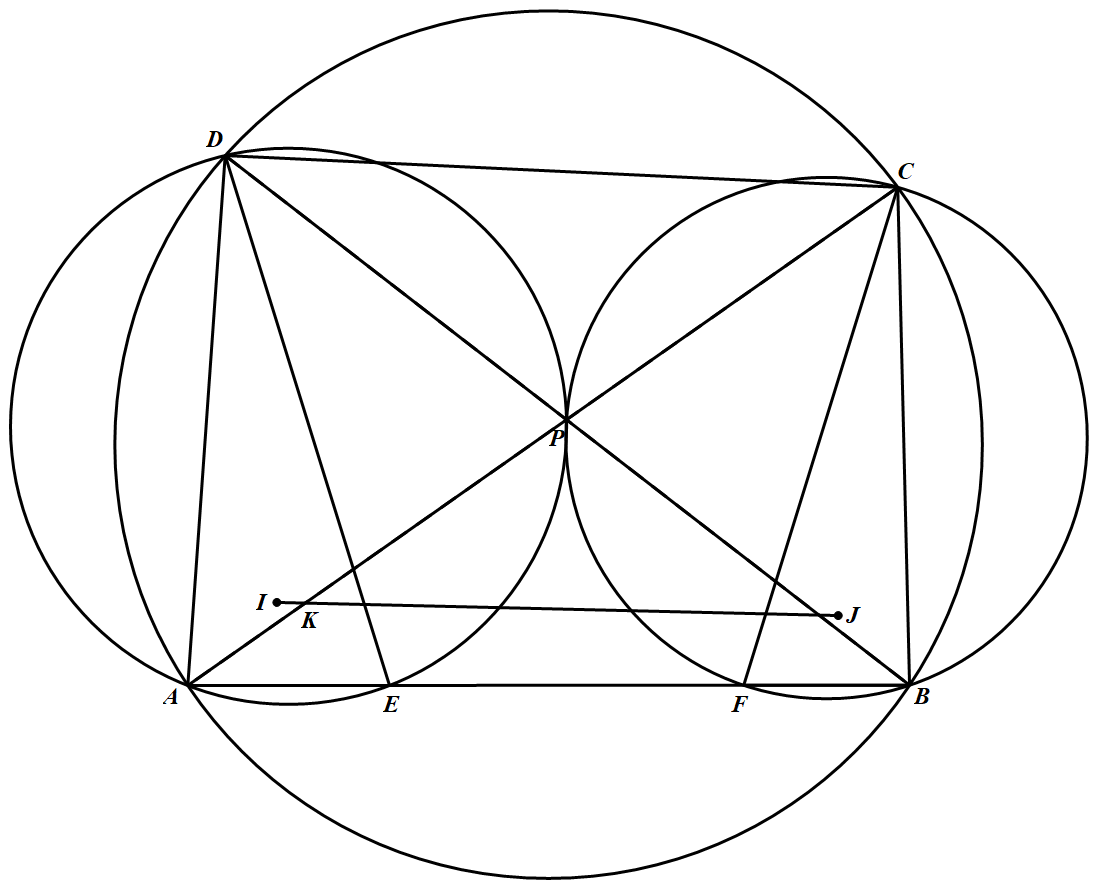
【难度】
【出处】
2017第33届CMO试题
【标注】
【答案】
略
【解析】
如图，延长 $EI$，与 $\triangle APD$ 的外接圆交于点 $X$；延长 $FJ$，与 $\triangle BPC$ 的外接圆交于点 $Y$，联结 $PX、PY、XA、YB$．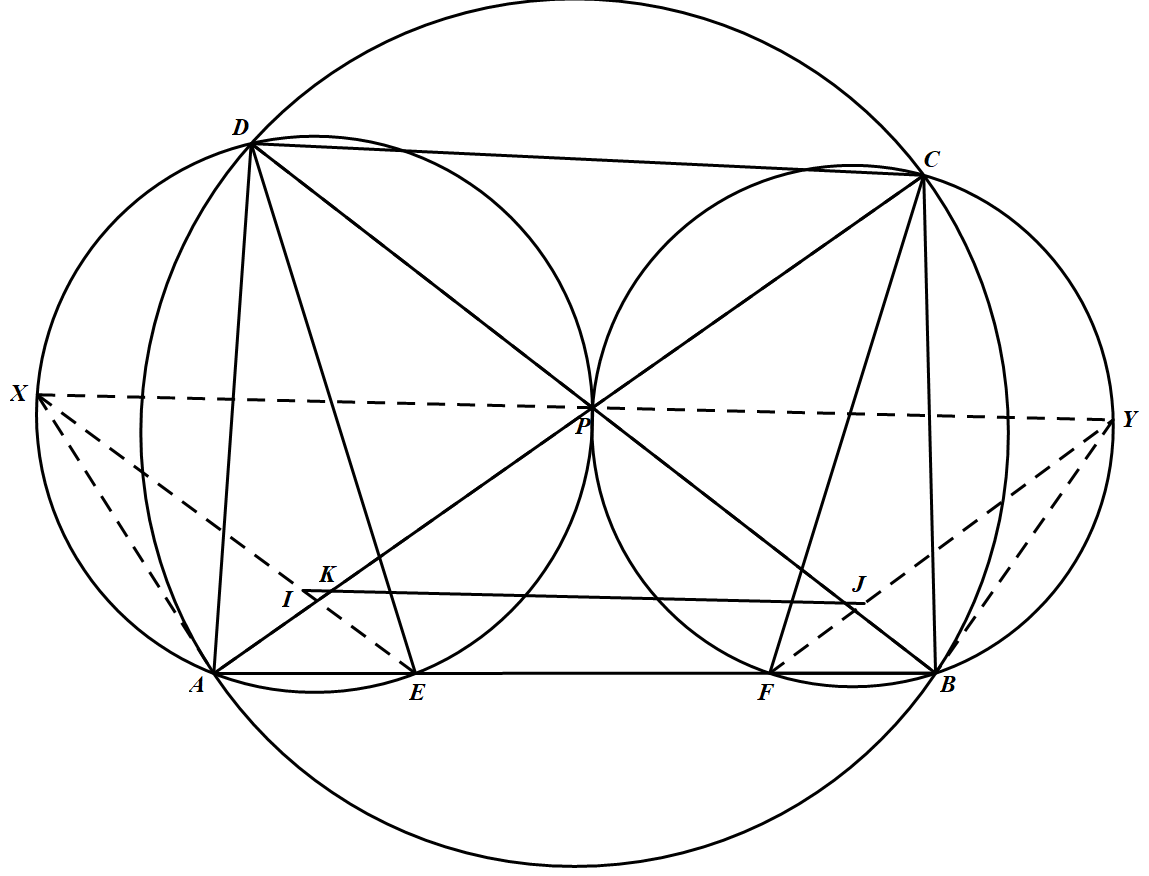
注意到，$l、J$ 分别为 $\triangle ADE、\triangle BCF$ 的内心．据内心性质知 $XI =XA,YJ = YB$．
易知，$PX、PY $ 分别为 $\angle APD、\angle BPC$ 的平分线．故 $X,P,Y$ 点共线．
由 $\angle A P X=\angle C P Y=\angle B P Y,\angle A X P=\angle A D P=\angle B C P=\angle B Y P$，知
$\triangle A P X \sim \triangle B P Y \Rightarrow \dfrac{X A}{Y B}=\dfrac{A P}{B P}\Rightarrow \dfrac{X I \sin \angle I X P}{YJ \sin \angle J Y P}\\=\dfrac{X A}{Y B} \cdot \dfrac{\sin \angle E A P}{\sin \angle F B P}=\dfrac{A P}{B P} \cdot \dfrac{\sin \angle B A P}{\sin \angle A B P}=1.$
这表明，点 $I、J $ 到直线 $XY$ 的距离相等注意到，$E、F$ 两点位于 $XY$ 的同侧．从而，$I、J$ 两点位于 $XY$ 的同侧，有 $IJ\parallel XY$．故 $\angle AKI=\angle APX=\angle AEI\Rightarrow A, I, K, E$ 四点共圆．
注意到，$l、J$ 分别为 $\triangle ADE、\triangle BCF$ 的内心．据内心性质知 $XI =XA,YJ = YB$．易知，$PX、PY $ 分别为 $\angle APD、\angle BPC$ 的平分线．故 $X,P,Y$ 点共线．
由 $\angle A P X=\angle C P Y=\angle B P Y,\angle A X P=\angle A D P=\angle B C P=\angle B Y P$，知
$\triangle A P X \sim \triangle B P Y \Rightarrow \dfrac{X A}{Y B}=\dfrac{A P}{B P}\Rightarrow \dfrac{X I \sin \angle I X P}{YJ \sin \angle J Y P}\\=\dfrac{X A}{Y B} \cdot \dfrac{\sin \angle E A P}{\sin \angle F B P}=\dfrac{A P}{B P} \cdot \dfrac{\sin \angle B A P}{\sin \angle A B P}=1.$
这表明，点 $I、J $ 到直线 $XY$ 的距离相等注意到，$E、F$ 两点位于 $XY$ 的同侧．从而，$I、J$ 两点位于 $XY$ 的同侧，有 $IJ\parallel XY$．故 $\angle AKI=\angle APX=\angle AEI\Rightarrow A, I, K, E$ 四点共圆．
答案
解析
备注
