2018第34届CMO试题

• 知识点

  >

  二试组合部分

略

解法一：先求最小值
（1）若 $a+b,b+c,c+d,d+e,e+a$ 中恰一个负数，不妨设 $a+b<0$，则 $a+b\geqslant -2,(b + c)(c + d)(d + e)(e + a)\leqslant(\dfrac{10 − a − b
}{4})^4\leqslant 81$ 从而原式 $\geqslant-162$．
（2）若 $ a + b, b + c, c + d, d + e,e + a $ 中恰 $3$ 个负数均 $\geqslant -2$，另外 $2$ 个非负数之和 $\leqslant 16$，故 $2$ 个非负数之积 $\geqslant 64$，从而原式 $\geqslant -512$．
又显然 $a + b, b + c, c + d, d + e, e + a$ 不能全负，故原式 $\geqslant -512$，当 $a = b = c = d = −1; e = 9$ 时取等．再求最大值
（1）若 $a+b, b+c, c+d, d+e, e+a$ 均为正，则原式 $\leqslant\left(\dfrac{2 a+2 b+2 c+2 d+2 e}{5}\right)^{5}=32$
（2）若 $a+b, b+c, c+d, d+e, e+a$ 中恰 $3$ 个正数，将若 $a+b, b+c, c+d, d+e, e+a$ 排成一个圆周，则必有 $2$ 个正数不相邻．
不妨设 $a+b, c+d>0$，则 $a+b+c+d=5-e \leqslant 6$，从而 $(a+b)(c+d) \leqslant 9$．
又显然 $a+b, b+c, c+d, d+e, e+a \in[-2,8]$，故原式 $\leqslant(-2)^{2} \times 9 \times 8=288$．
（3）若 $a+b, b+c, c+d, d+e, e+a$ 中恰一个正，不妨设 $a+b>0$，由 $(b+c)+(d+e) \leqslant 0$ 知 $a \geqslant 5$，由 $e \geqslant-1$，知 $e+a \geqslant 4$，矛盾．
综上，原式 $\leqslant 288$，当 $a=b=c=-1, d=e=4$ 时取等．
解法二
令 $a_{1}=a+b, \quad a_{2}=c+d, \quad a_{3}=e+a, \quad a_{4}=b+c, \quad a_{5}=d+e$ 则有 $\displaystyle \sum\limits_{i=1}^{5} a_{i}=2(a+b+c+d+e)=10$，所以 $a=5-a_{4}-a_{5}$，类似可表示出实数 $b, c, d, e$．因为 $a, b, c, d, e \geqslant-1 \Leftrightarrow a_{i}+a_{i+1} \leqslant 6\left(a_{6}=a_{1}\right)$
所以问题可转化为：
已知 $\displaystyle \sum a_{i}=10, a_{i}+a_{i+1} \leqslant 6\left(a_{6}=a_{1}\right)$，求 $\displaystyle \prod a_{i}$ 的最大值及最小值．对 $\left\{a_{i}\right\}$ 中哪些为正，哪些为负的情况讨论，轮换对称的情况只讨论一种；将 $a_i$ 放在正 $5$ 边形顶点上，对于所讨论的情况，非负标为红，负标为蓝，若有正 $5$ 边形的一个反射变换 $T$，使得所有 $a_i$ 与 $a_T(i)$ 颜色相同，则取极值时 $a_i=a_T(i)$，这是因为，将变量 $a_i$ 与 $a_T(i)$ 都换成相应的平均后，乘积绝对值变大，其它限制条件仍然满足，这个可以简化讨论过程．
（1）全红，乘积为正 $\displaystyle \prod\limits a_{i} \leqslant 2^{5}=32$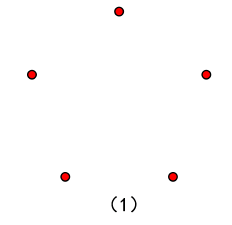 （2）一蓝四红
$\left\{\begin{array}{ll}{-x+2 y+2 z=10} \\ {-x+y \leqslant 6} {\Rightarrow x y^{2} z^{2} \leqslant x\left(\frac{y+z}{2}\right)^{4} \leqslant 2 \cdot\left(\frac{6}{2}\right)^{4}=162} \\ {y+z \leqslant 6}\end{array}\right.$
所以 $\displaystyle \prod\limits a_{i} \geqslant-162$，当 $\{a, b, c, d, e\}=\{-1,-1,4,-1,4\}$ 时取到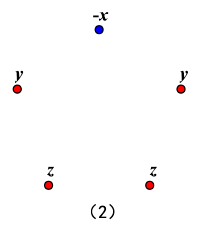（3）二蓝三红（i）
$\left\{\begin{array}{l}{y+z \leqslant 6} \\ {2 y+z=10+2 x \leqslant 12-z}\end{array} \Rightarrow 2 x+z \leqslant 2\right.$
由均值不等式 $x^{2} y^{2} z \leqslant\left(\dfrac{2}{3}\right)^{3} \cdot y^{2} \leqslant\left(\dfrac{2}{3}\right)^{3} \cdot 6^{2}<32$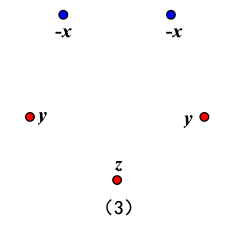（4）二蓝三红（ii）
$\left\{\begin{array}{l}{z \leqslant 3} \\ {y \leqslant 6+x \qquad \qquad y \leqslant 8} \\ {y+2 z=10+2 x}\end{array} \Rightarrow\left\{\begin{array}{l}{x \leqslant 2} \\ {y \leqslant 8} \\ {z \leqslant 3}\end{array}\right.\right.$ 则有 $x^{2} z^{2} y \leqslant 4 \cdot 9 \cdot 8=288$，当 $\{a, b, c, d, e\}=\{-1,-1,-1,4,4\}$ 时达到．（5）三蓝二红（i）
$\left\{\begin{array}{l}{x \leqslant 3} \\ {y \leqslant 2 \quad \Rightarrow x^{2} y^{2} z \leqslant 8 \cdot 9=72} \\ {z \leqslant 2}\end{array}\right.$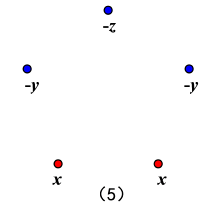（6）三蓝二红（ii）
$\left\{\begin{array}{l}{y, z \leqslant 2} \\ {x \leqslant 8}\end{array} \Rightarrow x^{2} y^{2} z \leqslant 2^{9}=512,\{a, b, c, d, e\}=\{-1,-1,-1,-1,9\}\right.$ 时达到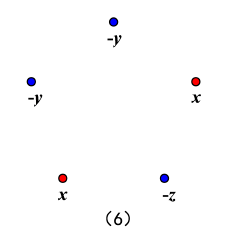（7）四蓝一红
由 $\left\{\begin{array}{l}{x \leqslant 6+y \leqslant 8} \\ {y, z \leqslant 2}\end{array}\right.$ 得 $x y^{2} z^{2} \leqslant 8 \cdot 2^{4}<288$
最大值为 $288$，$a,b,c,d,e$ 依次为 $-1,-1,-1,4,4$ 时达到；
最小值为 $-512$，$a, b, c, d, e$ 依次为 $-1,-1,-1,-1,9$ 时达到．