在 $\triangle ABC$ 中，$AB<AC$，$O$ 是三角形的外心，$D$ 是 $\angle BAC$ 角分线上一点，$E$ 在 $BC$ 上，满足 $OE\parallel AD$，$DE\bot BC$，在射线 $EB$ 上取一点 $K$，满足 $EK=EA$，$\triangle ADK$ 外接圆与 $BC$ 交于另外一点 $P\ne D$，$\triangle ADK$ 外接圆与 $\triangle ABC$ 外接圆交于另外一点 $Q\ne A$，求证：$PQ$ 与 $\triangle ABC$ 外接圆相切．
【难度】
【出处】
2018第34届CMO试题
【标注】
【答案】
略
【解析】
证法一
设 $O_2$ 为 $\triangle AKD$ 外心，$F$ 为 $AD$ 与 $\odot O$ 交点，则相切等价于 $\angle P Q A+\angle A B Q=180^{\circ}$．连结 $O O_{2}, O E, O_{2} E$．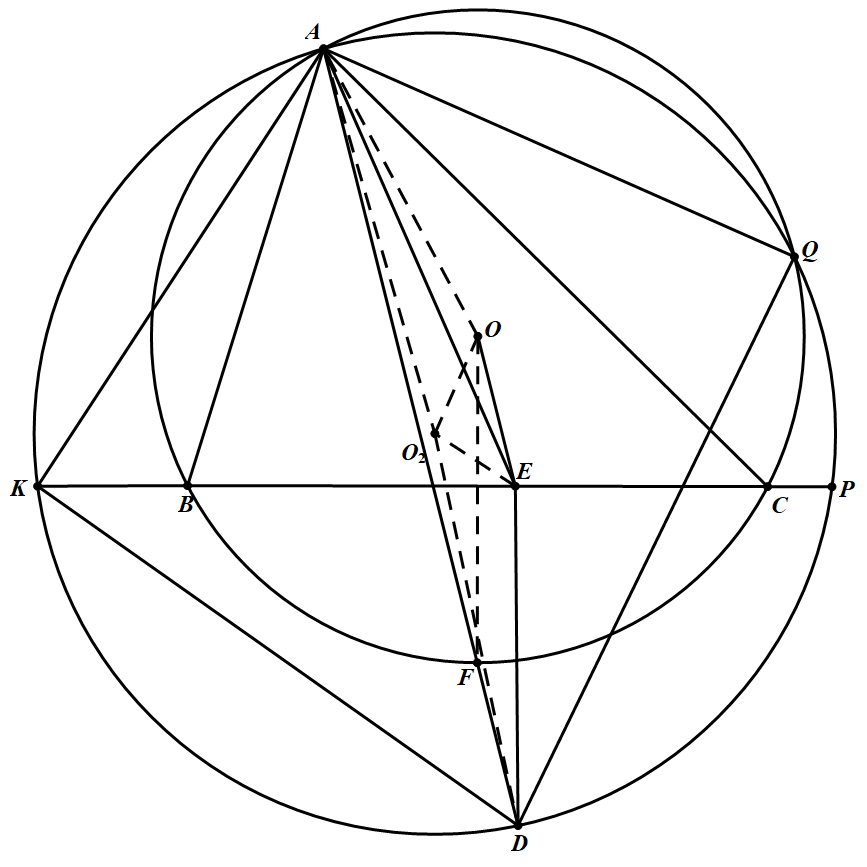
注意到 $O F \perp B C$，所以有 $O F \| E D$，所以四边形 $OFED$ 为平行四边形．
其次有 $A O=O F=D E$，所以有四边形 $AOED$ 为等腰梯形．
注意到 $O_{2} A=O_{2} D$，所以 $O_2$ 在 $OE$ 中垂线上，所以有 $\triangle O_{2} O E$ 为等腰三角形．
注意到 $\angle A B Q=\frac{1}{2} \angle A O Q=\angle A O_{2} O+\angle O_{2} A O$；
又 $E O_{2} \perp A K, E D \perp K C$，所以 $\angle A K C=180^{\circ}-\angle O_{2} E D=180^{\circ}-\angle O_{2} O A=\angle A B Q$．
证法二
思路分析：先尝试最自然的思路-消点法
已知条件略有些复杂，先根据题意用尺柜作出精确的图形，理解各个几何元素的生成过程．
（1）先作圆 $O$，任取三点 $A,B,C$ 使得 $AB<AC$
（2）过 $O$ 作 $BC$ 垂线交不含 $A$ 的 $\overparen{BC}$ 与 $S$，则 $AS$ 为 $\angle BAC$ 角平分线
（3）过 $E$ 作 $BC$ 垂线交 $AS$ 于 $D$
（4）在射线 $EB$ 上取点 $K$ 满足 $EK=EA$
（5）作 $\triangle ADK$ 外接圆交 $BC$ 于点 $P$，交圆 $O$ 于点 $Q$，连 $PQ$，图如下所示
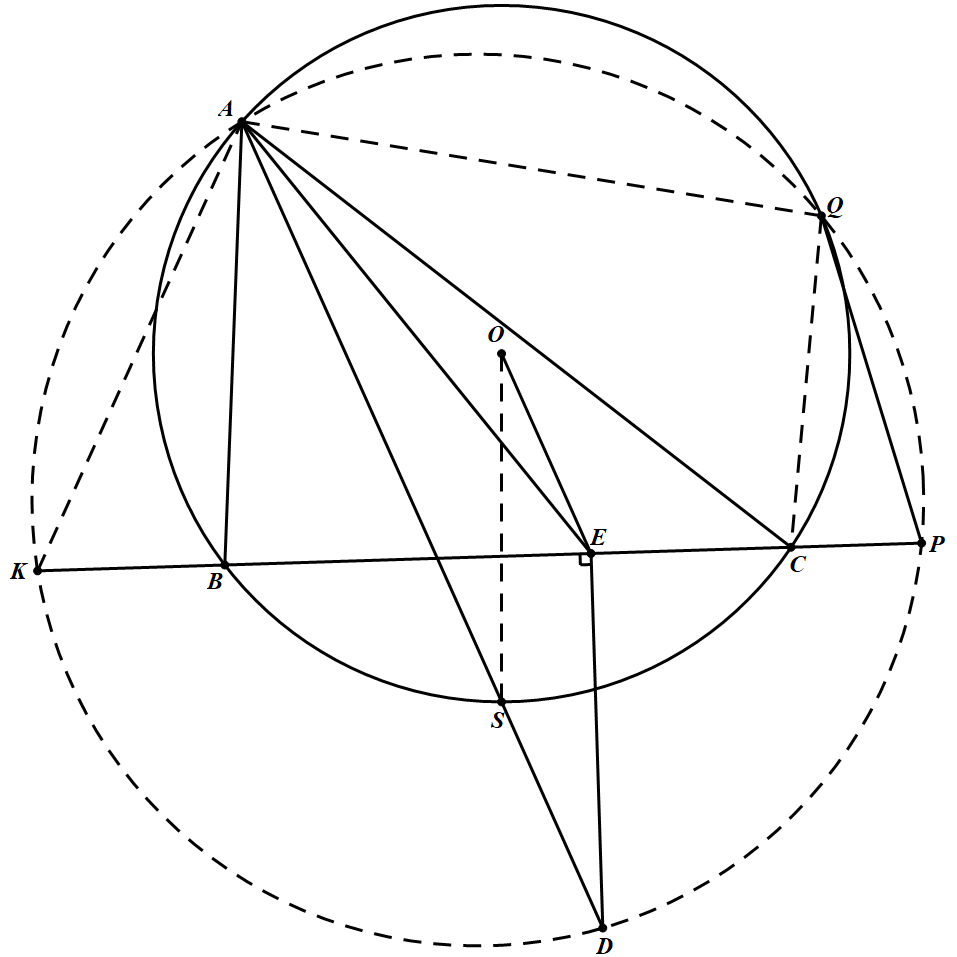下面由结果入手尽可能通过消点简化图形．
欲证 $PQ$ 为圆 $O$ 切线，即证 $\angle C Q P=\angle C A Q$．
由 $A, B, C, Q, A, K, P, Q$ 共圆得 $\angle C Q P=\angle A Q P-\angle A Q C=\left(180^{\circ}-\angle A K P\right)-\left(180^{\circ}-\angle A B P\right)=\angle A B P-\angle A K P=\angle B A K$
从而需证 $\angle B A K=\angle C A Q$，这样消去了点 $P$，这是一个进展的标志，思路应该有希望．消去 $P$，从而得到下图：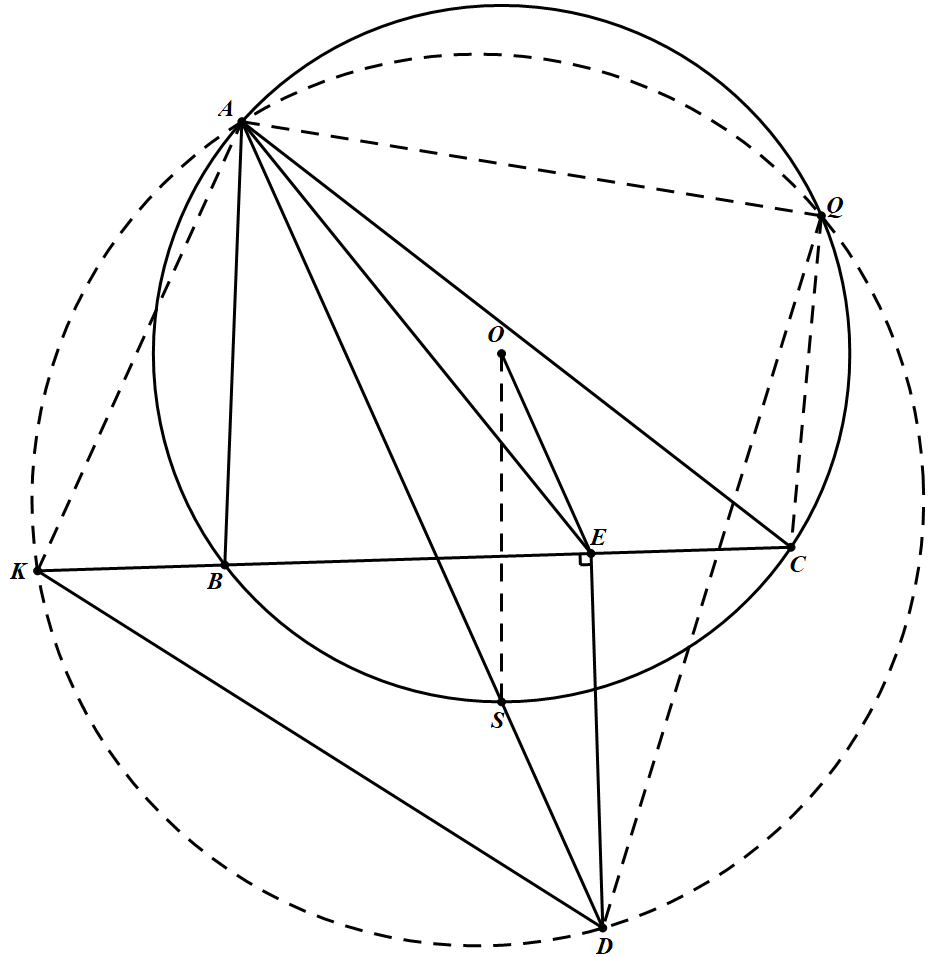
欲证 $\angle B A K=\angle C A Q$，而显然 $\angle A B K=\angle A Q C$，从而 $\triangle A B K \sim \triangle A Q C$，图形中显然最后生成的是点 $Q$，它最难描述，它是两圆交点，但是 $A,K,D,Q$ 共圆很难用，而 $\triangle A B K \sim \triangle A Q C$ 很好用．
考虑到点 $Q$ 的唯一性可以考虑用同一法，即在圆 $O$ 上取 $Q^\prime$ 使得 $\angle A B K=\angle A Q^{\prime} C$，下面只需证明 $A,K,D,Q^\prime$ 共圆即可，如下图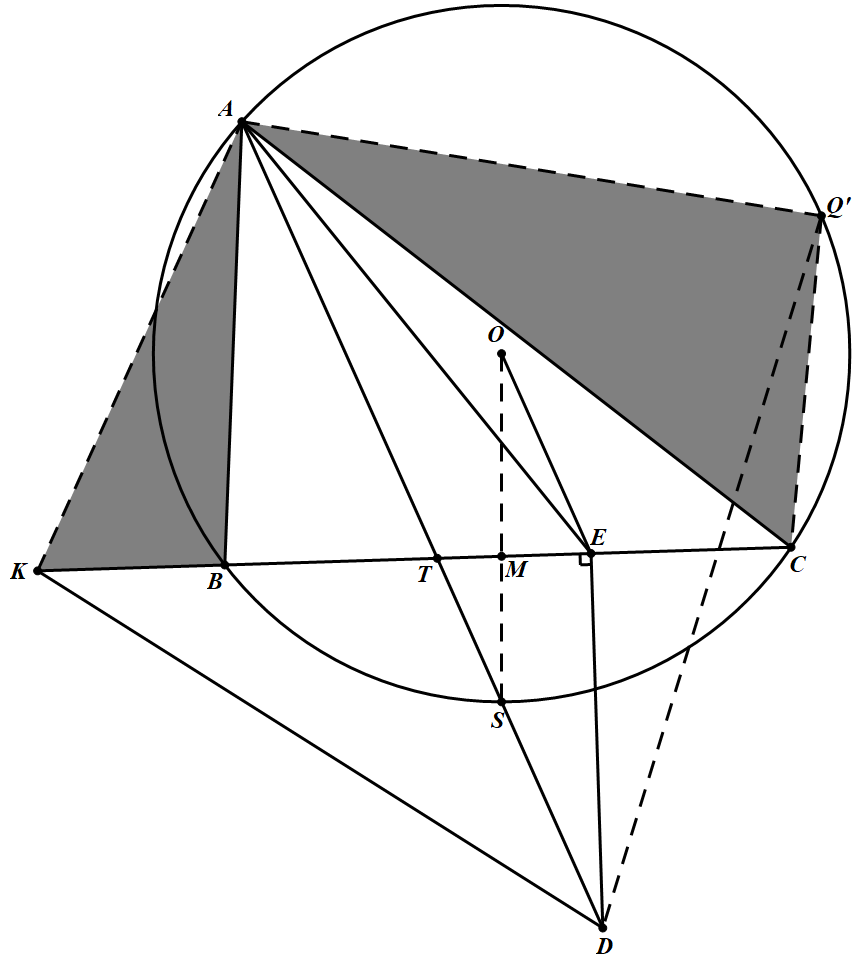
由 $\triangle A B K \sim \triangle A Q^{\prime} C$ 知 $A Q^{\prime} \cdot A K=A B \cdot A C$；
由 $\angle A B K=\angle A Q^{\prime} C$ 及 $AD$ 为 $\angle BAC$ 角平分线知 $\angle D A K=\angle D A Q^{\prime}=\theta$．
欲证 $A, K, D, Q^{\prime}$ 共圆，倒角希望渺茫，想到了托勒密定理的逆定理-三弦定理，即需证 $A K \cdot \sin \theta+A Q^{\prime} \cdot \sin \theta=A D \cdot \sin 2 \theta$
把 $AQ^\prime$ 代入，由二倍角公式即需证 $A K+A B \cdot A C / A K=2 A D \cdot \cos \theta$
即证 $A B \cdot A C=2 A D \cdot A K \cos \theta-A K^{2}$
这样消去了"讨厌"的点 $Q^\prime$，得到下图：
此时图穷匕见，图形已经不能化解，就必须面对点 $D$ 研究点 $D$ 的性质了．
由已知 $O E\|A D, O S\| D E$，则 $OSDE$ 为平行四边形，从而 $D E=O S=R$ 为圆 $O$ 半径，这个性质很简单，但是很漂亮，应该很重要．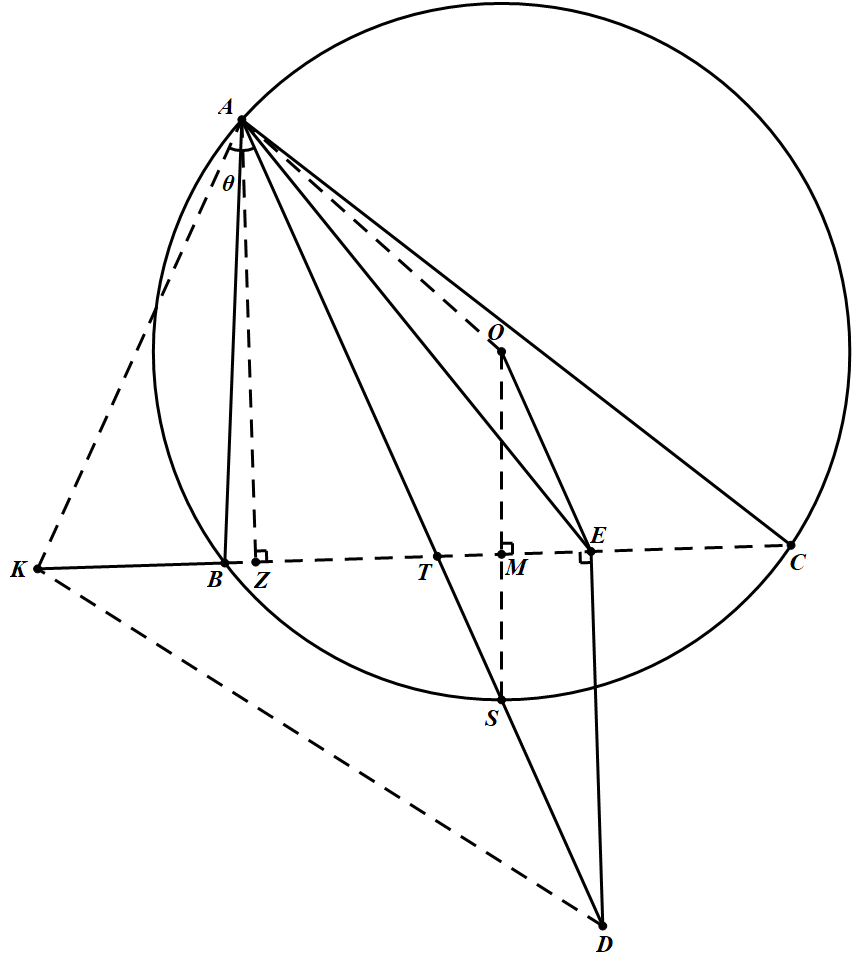
下面继续分析目标，即证 $A B \cdot A C=2 A D \cdot A K \cos \theta-A K^{2}$
后面的式子很像余弦定理，由余弦定理，从而需证 $A B \cdot A C=D A^{2}-D K^{2}$
我们希望用到条件 $EK=EA$ 及 $DE=R$，则在 $\triangle K D E$ 中由勾股定理，需证 $A B \cdot A C=D A^{2}-E K^{2}-E D^{2}$
即证 $A B \cdot A C=D A^{2}-E A^{2}-E D^{2}$
后面在 $\triangle ADE$ 中，又是一个余弦定理，从而需证 $A B \cdot A C=2 A E \cdot D E \sin \angle A E B=2 R \cdot A E \sin \angle A E B$
看到 $A E \sin \angle A E B$，自然的思路是作出高线 $AZ$，从而需证 $A B \cdot A C=2 R \cdot A Z$
这样就消去了点 $D,E,K$，得到下图的基本图形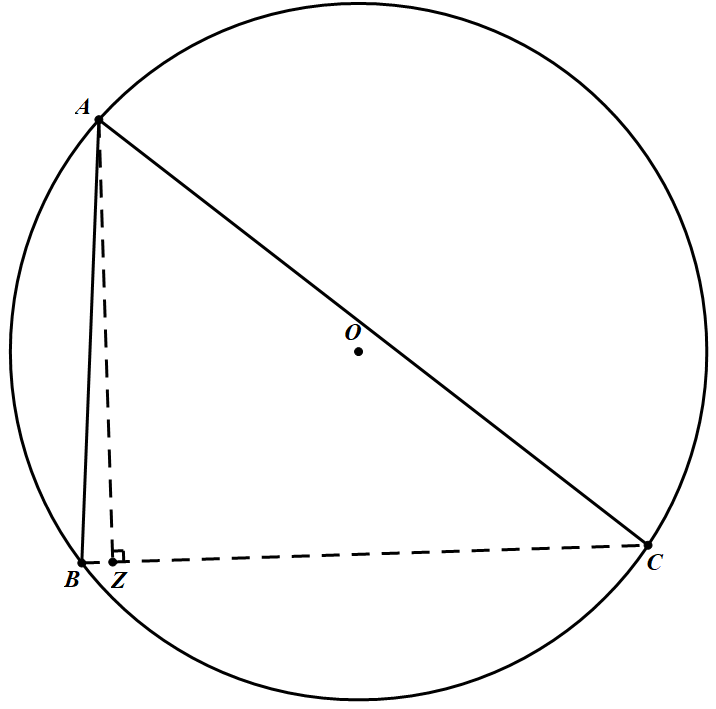
上述结果是一个非常简单而常见的经典结果，即可以利用正弦定理，也可以用相似．
例如由正弦定理 $A B \cdot A C=2 R \sin B \cdot A B=2 R \cdot A Z$ 从而完成了证明．
下面把详细过程书写如下：
如图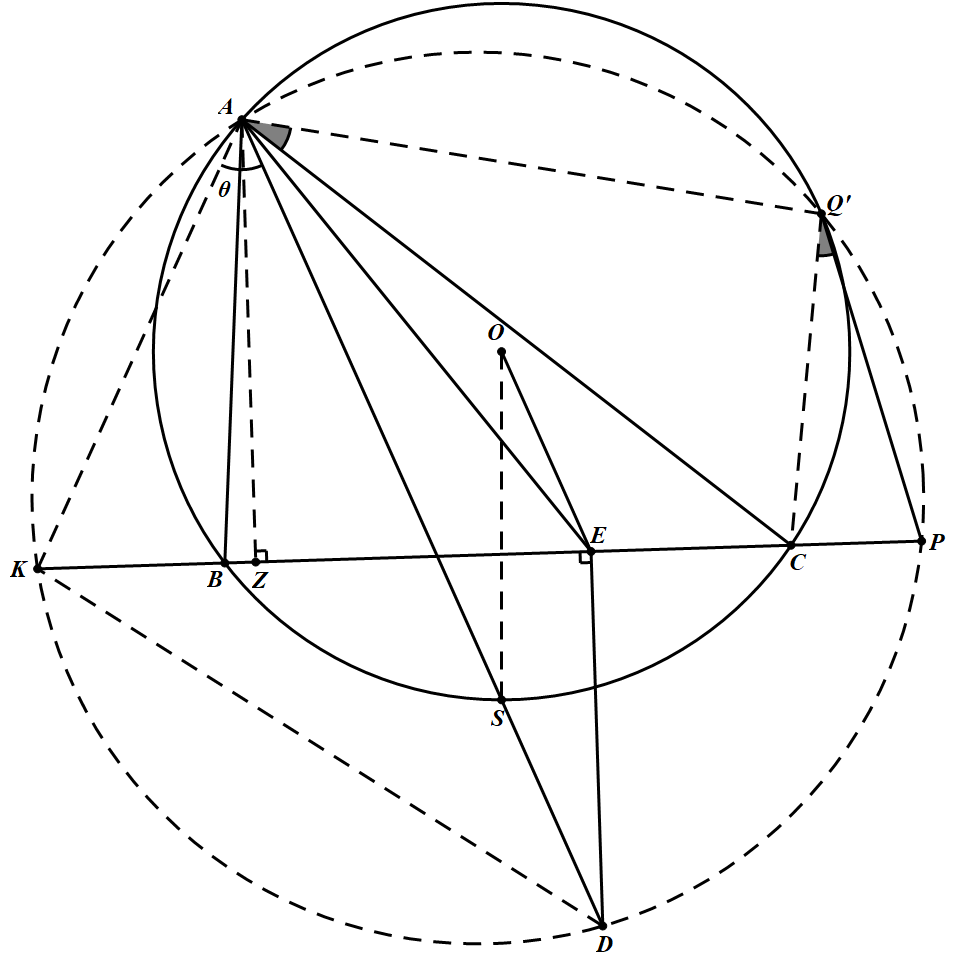
在圆 $O$ 上作 $Q^\prime$ 使 $\angle B A K=\angle C A Q^{\prime}$，设 $\angle S A K=\theta$，$AD$ 交圆 $O$ 于 $S$，作 $A Z \perp B C$ 于 $Z$．
由已知 $O E\|A D, O S\| D E$，则 $OSDE$ 为平行四边形，从而 $D E=O S=R$ 为圆 $O$ 半径，则
$ A B \cdot A C =2 R \sin B \cdot A B=2 R \cdot A Z=2 A E \cdot D E \sin \angle A E B=2 R \cdot A E \sin \angle A E B \\ =D A^{2}-E A^{2}-E D^{2}=D A^{2}-E K^{2}-E D^{2}=D A^{2}-D K^{2} =2 A D \cdot A K \cos \theta-A K^{2} $
由 $\triangle A B K \sim \triangle A Q^{\prime} C$ 知 $A Q^{\prime} \cdot A K=A B \cdot A C$；
由 $\angle A B K=\angle A Q^{\prime} C$ 及 $AD$ 为 $\angle BAC$ 角平分线知 $\angle D A K=\angle D A Q^{\prime}=\theta$，则 $A K \cdot \sin \theta+A Q^{\prime} \cdot \sin \theta=A D \cdot \sin 2 \theta$
由托勒密定理的逆定理-三弦定理知 $A, K, D, Q^{\prime}$ 共圆，故 $Q,Q^\prime$ 重合，故
$\begin{aligned} \angle C Q P &=\angle A Q P-\angle A Q C=\left(180^{\circ}-\angle A K P\right)-\left(180^{\circ}-\angle A B P\right) =\angle A B P-\angle A K P=\angle B A K=\angle C A Q \end{aligned}$
从而 $PQ$ 为圆 $O$ 的切线．
设 $O_2$ 为 $\triangle AKD$ 外心，$F$ 为 $AD$ 与 $\odot O$ 交点，则相切等价于 $\angle P Q A+\angle A B Q=180^{\circ}$．连结 $O O_{2}, O E, O_{2} E$．
注意到 $O F \perp B C$，所以有 $O F \| E D$，所以四边形 $OFED$ 为平行四边形．其次有 $A O=O F=D E$，所以有四边形 $AOED$ 为等腰梯形．
注意到 $O_{2} A=O_{2} D$，所以 $O_2$ 在 $OE$ 中垂线上，所以有 $\triangle O_{2} O E$ 为等腰三角形．
注意到 $\angle A B Q=\frac{1}{2} \angle A O Q=\angle A O_{2} O+\angle O_{2} A O$；
又 $E O_{2} \perp A K, E D \perp K C$，所以 $\angle A K C=180^{\circ}-\angle O_{2} E D=180^{\circ}-\angle O_{2} O A=\angle A B Q$．
证法二
思路分析：先尝试最自然的思路-消点法
已知条件略有些复杂，先根据题意用尺柜作出精确的图形，理解各个几何元素的生成过程．
（1）先作圆 $O$，任取三点 $A,B,C$ 使得 $AB<AC$
（2）过 $O$ 作 $BC$ 垂线交不含 $A$ 的 $\overparen{BC}$ 与 $S$，则 $AS$ 为 $\angle BAC$ 角平分线
（3）过 $E$ 作 $BC$ 垂线交 $AS$ 于 $D$
（4）在射线 $EB$ 上取点 $K$ 满足 $EK=EA$
（5）作 $\triangle ADK$ 外接圆交 $BC$ 于点 $P$，交圆 $O$ 于点 $Q$，连 $PQ$，图如下所示
下面由结果入手尽可能通过消点简化图形．欲证 $PQ$ 为圆 $O$ 切线，即证 $\angle C Q P=\angle C A Q$．
由 $A, B, C, Q, A, K, P, Q$ 共圆得 $\angle C Q P=\angle A Q P-\angle A Q C=\left(180^{\circ}-\angle A K P\right)-\left(180^{\circ}-\angle A B P\right)=\angle A B P-\angle A K P=\angle B A K$
从而需证 $\angle B A K=\angle C A Q$，这样消去了点 $P$，这是一个进展的标志，思路应该有希望．消去 $P$，从而得到下图：
欲证 $\angle B A K=\angle C A Q$，而显然 $\angle A B K=\angle A Q C$，从而 $\triangle A B K \sim \triangle A Q C$，图形中显然最后生成的是点 $Q$，它最难描述，它是两圆交点，但是 $A,K,D,Q$ 共圆很难用，而 $\triangle A B K \sim \triangle A Q C$ 很好用．考虑到点 $Q$ 的唯一性可以考虑用同一法，即在圆 $O$ 上取 $Q^\prime$ 使得 $\angle A B K=\angle A Q^{\prime} C$，下面只需证明 $A,K,D,Q^\prime$ 共圆即可，如下图
由 $\triangle A B K \sim \triangle A Q^{\prime} C$ 知 $A Q^{\prime} \cdot A K=A B \cdot A C$；由 $\angle A B K=\angle A Q^{\prime} C$ 及 $AD$ 为 $\angle BAC$ 角平分线知 $\angle D A K=\angle D A Q^{\prime}=\theta$．
欲证 $A, K, D, Q^{\prime}$ 共圆，倒角希望渺茫，想到了托勒密定理的逆定理-三弦定理，即需证 $A K \cdot \sin \theta+A Q^{\prime} \cdot \sin \theta=A D \cdot \sin 2 \theta$
把 $AQ^\prime$ 代入，由二倍角公式即需证 $A K+A B \cdot A C / A K=2 A D \cdot \cos \theta$
即证 $A B \cdot A C=2 A D \cdot A K \cos \theta-A K^{2}$
这样消去了"讨厌"的点 $Q^\prime$，得到下图：
此时图穷匕见，图形已经不能化解，就必须面对点 $D$ 研究点 $D$ 的性质了．由已知 $O E\|A D, O S\| D E$，则 $OSDE$ 为平行四边形，从而 $D E=O S=R$ 为圆 $O$ 半径，这个性质很简单，但是很漂亮，应该很重要．
下面继续分析目标，即证 $A B \cdot A C=2 A D \cdot A K \cos \theta-A K^{2}$后面的式子很像余弦定理，由余弦定理，从而需证 $A B \cdot A C=D A^{2}-D K^{2}$
我们希望用到条件 $EK=EA$ 及 $DE=R$，则在 $\triangle K D E$ 中由勾股定理，需证 $A B \cdot A C=D A^{2}-E K^{2}-E D^{2}$
即证 $A B \cdot A C=D A^{2}-E A^{2}-E D^{2}$
后面在 $\triangle ADE$ 中，又是一个余弦定理，从而需证 $A B \cdot A C=2 A E \cdot D E \sin \angle A E B=2 R \cdot A E \sin \angle A E B$
看到 $A E \sin \angle A E B$，自然的思路是作出高线 $AZ$，从而需证 $A B \cdot A C=2 R \cdot A Z$
这样就消去了点 $D,E,K$，得到下图的基本图形
上述结果是一个非常简单而常见的经典结果，即可以利用正弦定理，也可以用相似．例如由正弦定理 $A B \cdot A C=2 R \sin B \cdot A B=2 R \cdot A Z$ 从而完成了证明．
下面把详细过程书写如下：
如图
在圆 $O$ 上作 $Q^\prime$ 使 $\angle B A K=\angle C A Q^{\prime}$，设 $\angle S A K=\theta$，$AD$ 交圆 $O$ 于 $S$，作 $A Z \perp B C$ 于 $Z$．由已知 $O E\|A D, O S\| D E$，则 $OSDE$ 为平行四边形，从而 $D E=O S=R$ 为圆 $O$ 半径，则
$ A B \cdot A C =2 R \sin B \cdot A B=2 R \cdot A Z=2 A E \cdot D E \sin \angle A E B=2 R \cdot A E \sin \angle A E B \\ =D A^{2}-E A^{2}-E D^{2}=D A^{2}-E K^{2}-E D^{2}=D A^{2}-D K^{2} =2 A D \cdot A K \cos \theta-A K^{2} $
由 $\triangle A B K \sim \triangle A Q^{\prime} C$ 知 $A Q^{\prime} \cdot A K=A B \cdot A C$；
由 $\angle A B K=\angle A Q^{\prime} C$ 及 $AD$ 为 $\angle BAC$ 角平分线知 $\angle D A K=\angle D A Q^{\prime}=\theta$，则 $A K \cdot \sin \theta+A Q^{\prime} \cdot \sin \theta=A D \cdot \sin 2 \theta$
由托勒密定理的逆定理-三弦定理知 $A, K, D, Q^{\prime}$ 共圆，故 $Q,Q^\prime$ 重合，故
$\begin{aligned} \angle C Q P &=\angle A Q P-\angle A Q C=\left(180^{\circ}-\angle A K P\right)-\left(180^{\circ}-\angle A B P\right) =\angle A B P-\angle A K P=\angle B A K=\angle C A Q \end{aligned}$
从而 $PQ$ 为圆 $O$ 的切线．
答案
解析
备注
