如图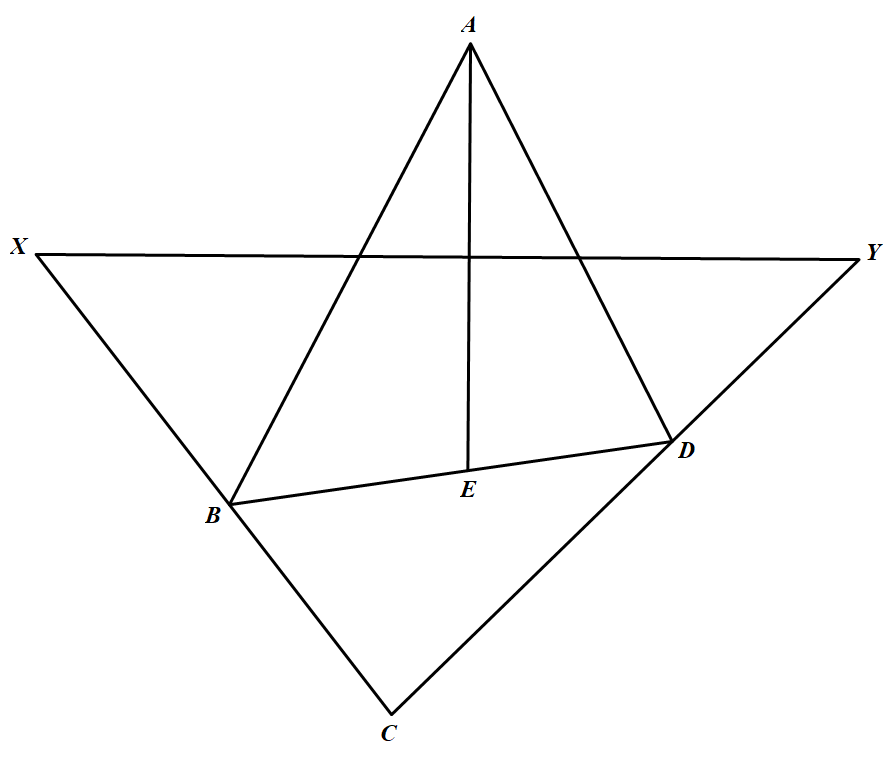
在凸四边形 $ABCD$ 中，$\angle B A D+2 \angle B C D=180^{\circ}$，$\angle B A D$ 的平分线交线段 $BD$ 于点 $E$，线段 $AE$ 的中垂线与直线 $CB、CD$ 分别交于点 $X、Y$．
证明：$A、X、C, Y$ 四点共圆．
在凸四边形 $ABCD$ 中，$\angle B A D+2 \angle B C D=180^{\circ}$，$\angle B A D$ 的平分线交线段 $BD$ 于点 $E$，线段 $AE$ 的中垂线与直线 $CB、CD$ 分别交于点 $X、Y$．证明：$A、X、C, Y$ 四点共圆．
【难度】
【出处】
2017第16届CGMO试题
【标注】
【答案】
略
【解析】
证法一
如图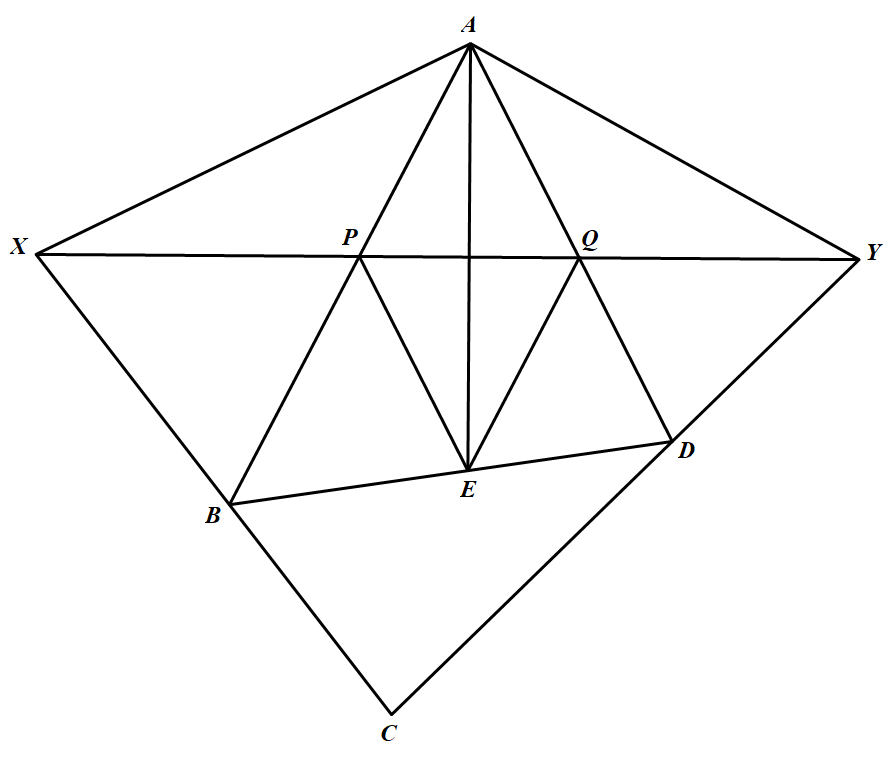
设 $X,Y$ 分别与 $AB,AD$ 相交于点 $P,Q$，连结 $EP、EQ$．由于 $PQ$ 垂直于 $\angle BAD$ 的平分线 $AE$，故 $\angle A P Q=\angle A Q P$，因此 $A P=A Q$．由于 $P,Q$ 均在 $AE$ 的中垂线上．故 $A P=E P, A Q=E Q$．因此四边形 $APEQ$ 的四边长均相等，即四边形 $APEQ$ 是菱形．
由于 $ \angle P X B =180^{\circ}-\angle C-\angle Q Y C =90^{\circ}+\angle F A D-\angle Q Y C =\angle A Q Y-\angle Q Y C=\angle Q D Y $
又 $\angle X P B=\angle A P Q=\angle A Q P=\angle D Q Y$，故 $\triangle X P B \sim \triangle D Q Y$．因此 $\dfrac{P X}{P B}=\dfrac{Q D}{Q Y}$．即 $P X \cdot Q Y=P B \cdot Q D$．由四边形 $ APEQ$ 是菱形知 $PE\parallel AD, QE \parallel AB$，故 $\dfrac{P B}{P E}=\dfrac{A B}{A D}=\dfrac{Q E}{Q D}$．
因此 $P A \cdot Q A=P E \cdot Q E=P B \cdot Q D=P X \cdot Q Y$，即 $\dfrac{P A}{P X}=\dfrac{Q Y}{Q A}$．结合 $\angle A P X=180^{\circ}-\angle A P Q=180^{\circ}-\angle A Q P=\angle Y Q A$，知 $\triangle A P X \sim \triangle \triangle Y Q A$，因此
$ \angle X A Y =\angle X A Q+\angle Y A Q =\angle X A Q+\angle A X Q =180^{\circ}-\angle A Q X $，又 $\angle C=90^{\circ}-\angle E A D=\angle A Q X$，故 $\angle X A Y+\angle C=180^{\circ}$，即 $A, X, C, Y$ 四点共圆．
证法二
如图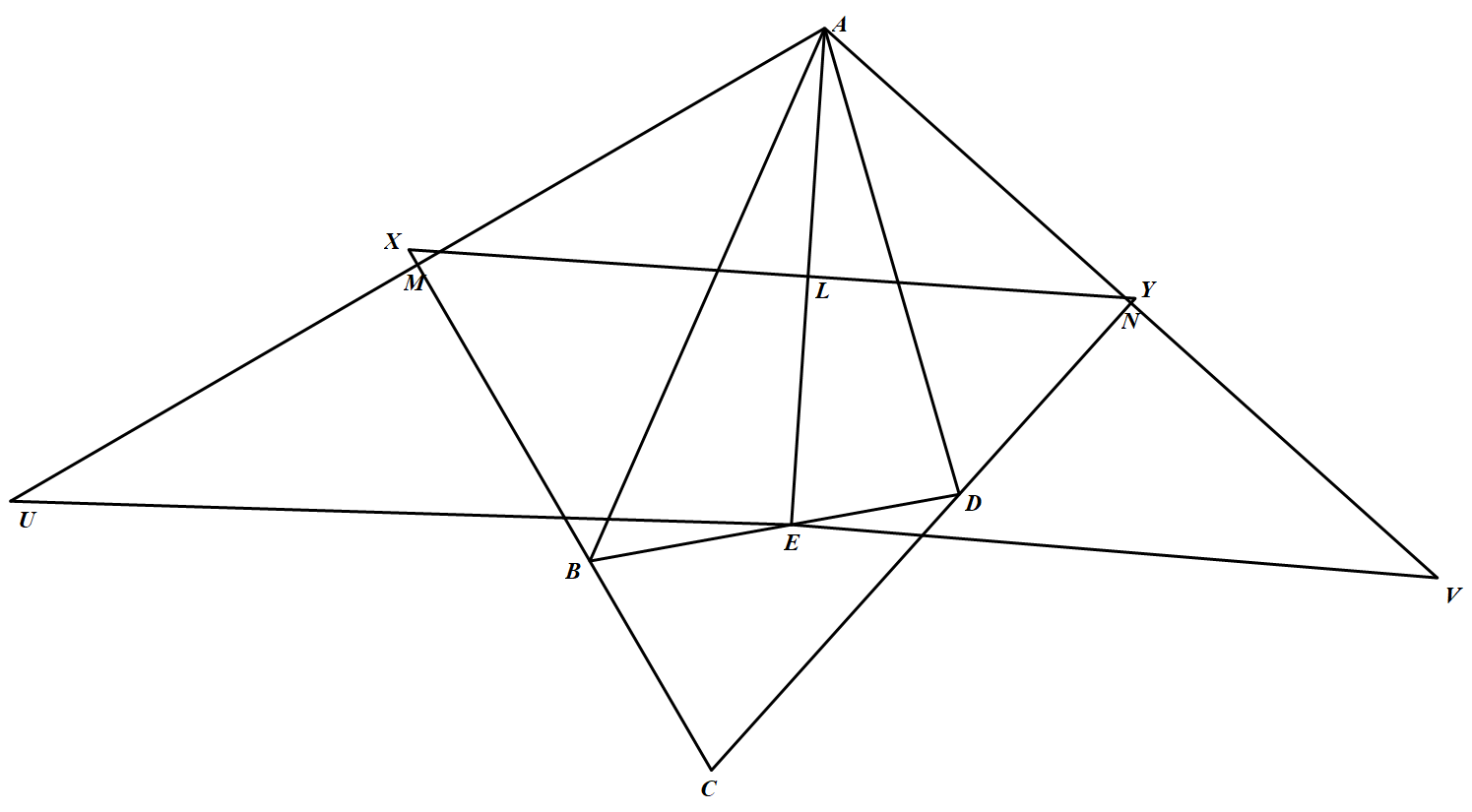
设 $L、M、N$ 分别为点 $A$ 到直线 $XY、BC、CD$ 的垂足，$U、V$ 分别为点 $A$ 关于直线 $BC、CD$ 的对称点．为证明 $A、X、C、Y$ 四点共 圆，由西姆松逆定理知只需证明 $L、M、N$ 三点共线．显然 $L、M、N$ 分别是线段 $AE、AU、AV$ 的中点．故只需证明 $E、U、V$ 三点共线由于 $\dfrac{B U}{B E}=\dfrac{A B}{B E}=\dfrac{A D}{D E}=\dfrac{D V}{D E}$，又
$ \angle U B X+\angle X B D+\angle B D Y+\angle Y D V =\angle A B X+180^{\circ}+\angle B C D+\angle A D Y \\=540^{\circ}+\angle B C D-\angle A B C-\angle A D C =180^{\circ}+\angle B A D+2 \angle B C D =360^{\circ}$
故 $U、V$ 在直线 $BD$ 的两侧，且 $\angle UBE=\angle VDE$．因此 $\triangle UBE \sim \triangle VDE$，故 $\angle BEU=\angle DEV$，结合 $U、V$ 在直线 $BD$ 的两侧知 $E、U、V$ 三点共线．故有 $A、X、C、Y$ 四点共圆．
如图
设 $X,Y$ 分别与 $AB,AD$ 相交于点 $P,Q$，连结 $EP、EQ$．由于 $PQ$ 垂直于 $\angle BAD$ 的平分线 $AE$，故 $\angle A P Q=\angle A Q P$，因此 $A P=A Q$．由于 $P,Q$ 均在 $AE$ 的中垂线上．故 $A P=E P, A Q=E Q$．因此四边形 $APEQ$ 的四边长均相等，即四边形 $APEQ$ 是菱形．由于 $ \angle P X B =180^{\circ}-\angle C-\angle Q Y C =90^{\circ}+\angle F A D-\angle Q Y C =\angle A Q Y-\angle Q Y C=\angle Q D Y $
又 $\angle X P B=\angle A P Q=\angle A Q P=\angle D Q Y$，故 $\triangle X P B \sim \triangle D Q Y$．因此 $\dfrac{P X}{P B}=\dfrac{Q D}{Q Y}$．即 $P X \cdot Q Y=P B \cdot Q D$．由四边形 $ APEQ$ 是菱形知 $PE\parallel AD, QE \parallel AB$，故 $\dfrac{P B}{P E}=\dfrac{A B}{A D}=\dfrac{Q E}{Q D}$．
因此 $P A \cdot Q A=P E \cdot Q E=P B \cdot Q D=P X \cdot Q Y$，即 $\dfrac{P A}{P X}=\dfrac{Q Y}{Q A}$．结合 $\angle A P X=180^{\circ}-\angle A P Q=180^{\circ}-\angle A Q P=\angle Y Q A$，知 $\triangle A P X \sim \triangle \triangle Y Q A$，因此
$ \angle X A Y =\angle X A Q+\angle Y A Q =\angle X A Q+\angle A X Q =180^{\circ}-\angle A Q X $，又 $\angle C=90^{\circ}-\angle E A D=\angle A Q X$，故 $\angle X A Y+\angle C=180^{\circ}$，即 $A, X, C, Y$ 四点共圆．
证法二
如图
设 $L、M、N$ 分别为点 $A$ 到直线 $XY、BC、CD$ 的垂足，$U、V$ 分别为点 $A$ 关于直线 $BC、CD$ 的对称点．为证明 $A、X、C、Y$ 四点共 圆，由西姆松逆定理知只需证明 $L、M、N$ 三点共线．显然 $L、M、N$ 分别是线段 $AE、AU、AV$ 的中点．故只需证明 $E、U、V$ 三点共线由于 $\dfrac{B U}{B E}=\dfrac{A B}{B E}=\dfrac{A D}{D E}=\dfrac{D V}{D E}$，又$ \angle U B X+\angle X B D+\angle B D Y+\angle Y D V =\angle A B X+180^{\circ}+\angle B C D+\angle A D Y \\=540^{\circ}+\angle B C D-\angle A B C-\angle A D C =180^{\circ}+\angle B A D+2 \angle B C D =360^{\circ}$
故 $U、V$ 在直线 $BD$ 的两侧，且 $\angle UBE=\angle VDE$．因此 $\triangle UBE \sim \triangle VDE$，故 $\angle BEU=\angle DEV$，结合 $U、V$ 在直线 $BD$ 的两侧知 $E、U、V$ 三点共线．故有 $A、X、C、Y$ 四点共圆．
答案
解析
备注
