如图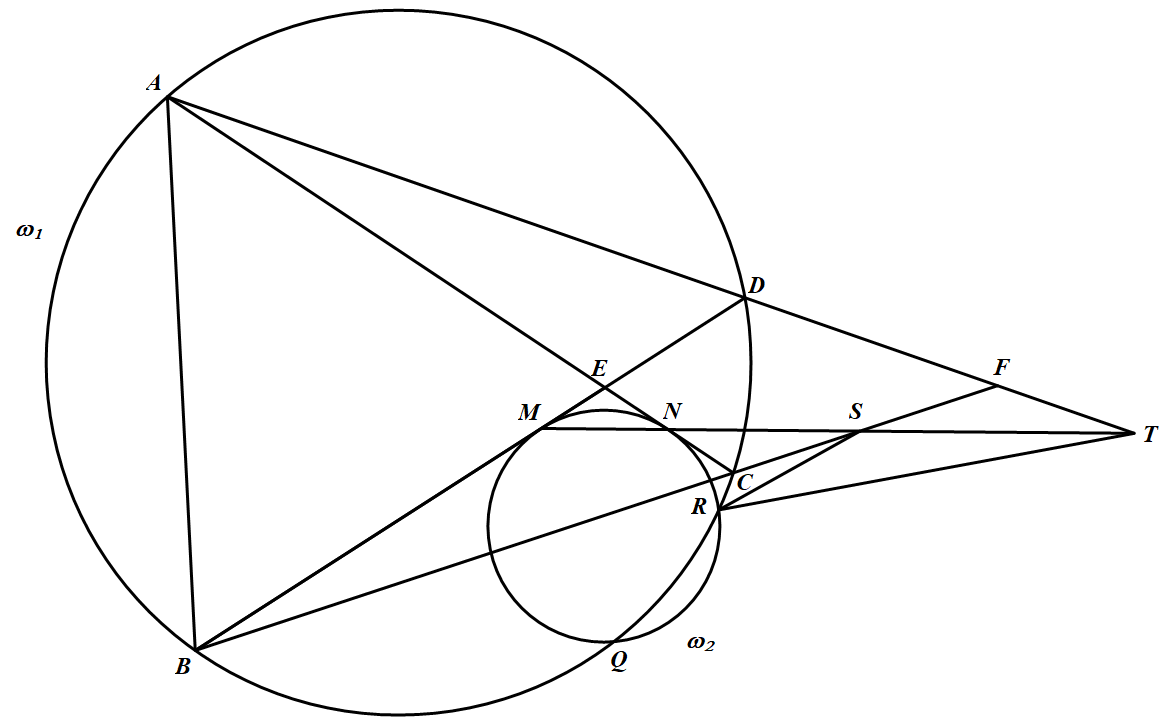
圆 $\omega_1$ 是四边形 $ABCD$ 的外接圆，$AC$ 交 $BD$ 于 $E$，$AD$ 交 $BC$ 于 $F$．圆 $\omega_2$ 分别与线段 $ EB、EC$ 相切于点 $M、N$，且与圆 $\omega_1$ 相交于 $Q、R$ 两点，直线 $BC、AD$ 分别交直线 $MN $ 于点 $S、T$．
求证：$Q,R,S,T$ 四点共圆．
圆 $\omega_1$ 是四边形 $ABCD$ 的外接圆，$AC$ 交 $BD$ 于 $E$，$AD$ 交 $BC$ 于 $F$．圆 $\omega_2$ 分别与线段 $ EB、EC$ 相切于点 $M、N$，且与圆 $\omega_1$ 相交于 $Q、R$ 两点，直线 $BC、AD$ 分别交直线 $MN $ 于点 $S、T$．求证：$Q,R,S,T$ 四点共圆．
【难度】
【出处】
2017第16届CGMO试题
【标注】
【答案】
略
【解析】
证法一
如图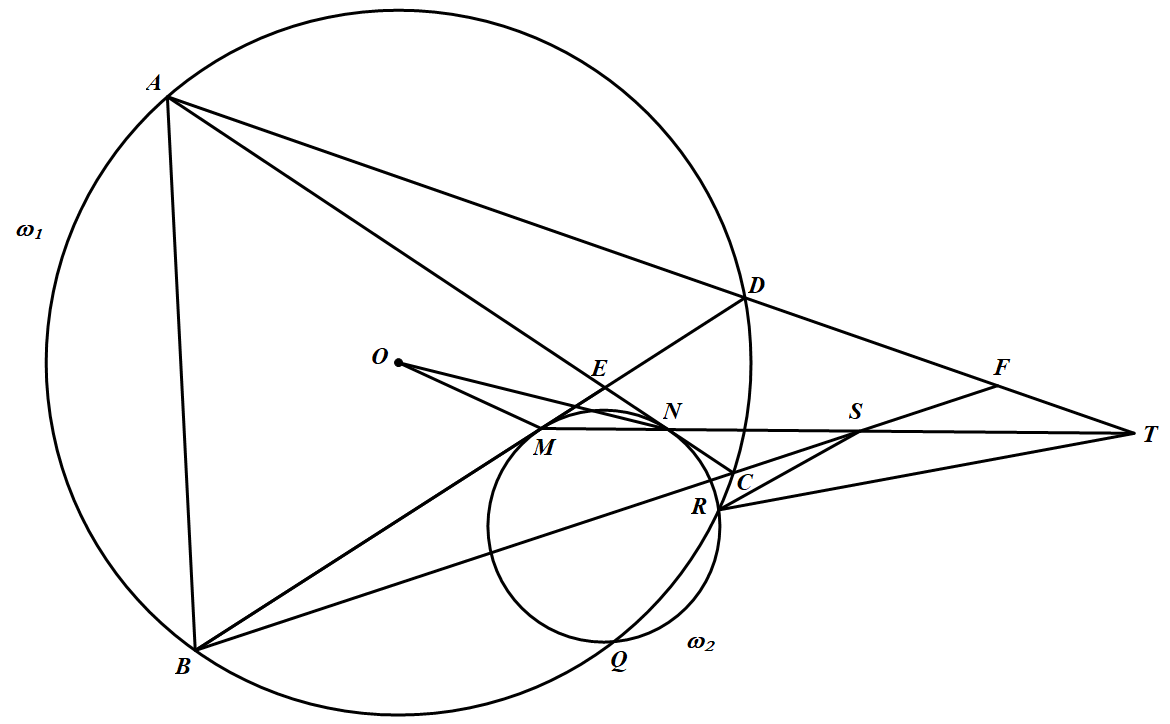
设 $MN=a,NS=b,ST=c$，$\omega_1$ 的圆心为 $O$，半径为 $r$．由于
$\begin{aligned} \angle D T M &=\angle E N M-\angle N A T =\angle E M N-\angle M B S =\angle C S N \end{aligned}$，
又 $\angle D M T=\angle E N M=\angle C N T$，故 $\triangle D M T \sim \triangle C N S$；由于 $\angle A T N=\angle D T M=\angle C S N=\angle B S M, \angle T A N=\angle S B M$，故 $\triangle A N T \sim \triangle B M S$．因此，$\dfrac{A N}{b+c}=\dfrac{B M}{a+b}, \dfrac{C N}{b}=\dfrac{D M}{a+b+c}$，故 $\dfrac{A N \cdot C N}{b(b+c)}=\dfrac{B M \cdot D M}{(a+b)(a+b+c)}$，设此比值为 $\lambda$，则
$Q M^{2}=r^{2}-B M \cdot M D=r^{2}-\lambda(a+b)(a+b+c),O N^{2}=r^{2}-A N \cdot C N=r^{2}-\lambda b(b+c)$
设 $QR,MN$ 交于点 $K$，并设 $NK=x$，则 $O K^{2}=r^{2}+K R \cdot K Q=r^{2}+K M \cdot K N=r^{2}+x(a+x)$．由于 $N$ 为 $\triangle OMK$（可能退化）的 $MK$ 边上的点，由斯台沃特定理得 $\mathrm{OM}^{2} \cdot \mathrm{NK}+\mathrm{OK}^{2} \cdot \mathrm{MN}=\mathrm{ON}^{2} \cdot \mathrm{MK}+\mathrm{MN} \cdot \mathrm{NK} \cdot \mathrm{MK}$，此即 $x\left[r^{2}-\lambda(a+b)(a+b+c)\right]+a\left[r^{2}+x(a+x)\right]=(a+x)\left[r^{2}-\lambda b(b+c)\right]+a x(a+x)$
两边同时减去 $(a+x) r^{2}+a x(a+x)$ 得 $-\lambda x(a+b)(a+b+c)=-\lambda(a+x) b(b+c)$．因此，$x(a+b)(a+b+c)=(a+x) b(b+c)$，故
$x=\dfrac{a b(b+c)}{(a+b)(a+b+c)-b(b+c)}=\dfrac{b(b+c)}{a+2 b+c},M K \cdot N K-S K \cdot T K=x(a+x)-(b-x)(b+c-x)=x(a+2 b+c)-b(b+c)=0$
因此，$S K \cdot T K=M K \cdot N K=Q K \cdot R K$，故 $Q、R、S、T$ 四点共圆．
证法二
首先 $\angle D T M=\angle E N M-\angle N A T=\angle E M N-\angle M B S=\angle C S N$，故 $\angle F S T=\angle C S N=\angle D T M=\angle F T S$，因此 $F S=F T$．由正弦定理知
$\dfrac{A T}{A N}=\dfrac{\sin \angle A N T}{\sin \angle A^{\prime} T^{\prime} N}, \dfrac{B S}{B M}=\dfrac{\sin \angle B M S}{\sin \angle B S M}$
$\dfrac{C S}{C N}=\dfrac{\sin \angle C N S}{\sin \angle C S N}, \dfrac{D T}{D M}=\dfrac{\sin \angle D M T}{\sin \angle D T M}$ ①
由于 $\angle A T N=\angle D T M=\angle C S N=\angle B S M$．又 $180^{\circ}-\angle B M S=\angle D M T=\angle A N M=\angle C N S=180^{\circ}-\angle A N T$，
故 ① 式中每个等式右边的分子和分母均相同，因此 $\dfrac{A T}{A N}=\dfrac{B S}{B M}=\dfrac{C S}{C N}=\dfrac{D T}{D M}$．
设此比值为 $k$．记 $\omega_3$ 为与 $ FS、FT$ 分别切于点 $S、T$ 的圆（由 $FS = FT$ 知此 圆存在）．如图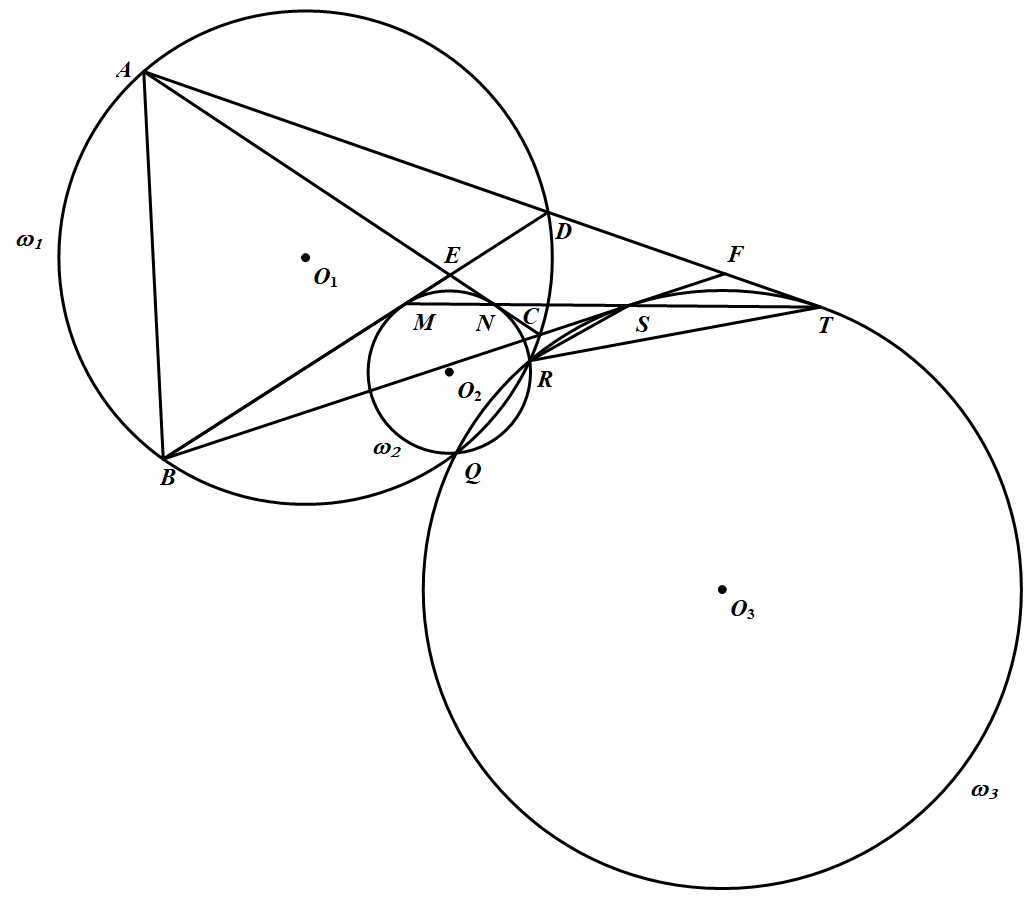
，设 $\omega_{1}, \omega_{2}, \omega_{3}$ 的圆心分别为 $O_{1}, O_{2}, O_{3}$，半径分别为 $r_1, r_2 , r_3$．对平面上任意一点 $ P$，定义 $f(P)=\left(k^{2}-1\right)\left(P O_{1}^{2}-r_{1}^{2}\right)-k^{2}\left(P\left(O_{2}^{2}-r_{2}^{2}\right)+\left(P O_{3}^{2}-r_{3}^{2}\right)\right.$．
那么 $f(A)=\left(k^{2}-1\right) \cdot 0-k^{2} \cdot A N^{2}+A T^{2}=0$，同理 $f(B)=f(C)=f(D)=0$．建立平面直角坐标系，设 $O_i$ 的坐标为 $\left(x_{i}, y_{i}\right)(i=1,2,3)$，则
$ f(x, y)=\left(k^{2}-1\right)\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}-r_{1}^{2}\right] -k^{2}\left[\left(x-x_{2}\right)^{2}+\left(y-y_{2}\right)^{2}-r_{2}^{2}\right] +\left[\left(x-x_{3}\right)^{2}+\left(y-y_{3}\right)^{2}-r_{3}^{2}\right] = a x+b y+c $（$a,b,c$ 为常数）
若 $a、b、c$ 不全为零，则满足 $f(x, y) = 0$ 的点 $(x, y)$（若存在）的轨迹是 一条直线，但此直线须过 $A,B,C,D $ 四个点，矛盾！因此 $a = b=c = d = 0$，即 $f$ 恒为 $ 0$．由 $RO_1^2 = r_1^2, RO_2^2= r_2^2$ 及 $f(R)= 0$ 知 $RO_3^2 = r_3^2$．即 $ R $ 在 $\omega_3$ 上．同理，$ Q $ 在 $ \omega_3 $ 上．因此 $ Q、R、S、T $ 四点共圆 $ \omega_3$．
如图
设 $MN=a,NS=b,ST=c$，$\omega_1$ 的圆心为 $O$，半径为 $r$．由于$\begin{aligned} \angle D T M &=\angle E N M-\angle N A T =\angle E M N-\angle M B S =\angle C S N \end{aligned}$，
又 $\angle D M T=\angle E N M=\angle C N T$，故 $\triangle D M T \sim \triangle C N S$；由于 $\angle A T N=\angle D T M=\angle C S N=\angle B S M, \angle T A N=\angle S B M$，故 $\triangle A N T \sim \triangle B M S$．因此，$\dfrac{A N}{b+c}=\dfrac{B M}{a+b}, \dfrac{C N}{b}=\dfrac{D M}{a+b+c}$，故 $\dfrac{A N \cdot C N}{b(b+c)}=\dfrac{B M \cdot D M}{(a+b)(a+b+c)}$，设此比值为 $\lambda$，则
$Q M^{2}=r^{2}-B M \cdot M D=r^{2}-\lambda(a+b)(a+b+c),O N^{2}=r^{2}-A N \cdot C N=r^{2}-\lambda b(b+c)$
设 $QR,MN$ 交于点 $K$，并设 $NK=x$，则 $O K^{2}=r^{2}+K R \cdot K Q=r^{2}+K M \cdot K N=r^{2}+x(a+x)$．由于 $N$ 为 $\triangle OMK$（可能退化）的 $MK$ 边上的点，由斯台沃特定理得 $\mathrm{OM}^{2} \cdot \mathrm{NK}+\mathrm{OK}^{2} \cdot \mathrm{MN}=\mathrm{ON}^{2} \cdot \mathrm{MK}+\mathrm{MN} \cdot \mathrm{NK} \cdot \mathrm{MK}$，此即 $x\left[r^{2}-\lambda(a+b)(a+b+c)\right]+a\left[r^{2}+x(a+x)\right]=(a+x)\left[r^{2}-\lambda b(b+c)\right]+a x(a+x)$
两边同时减去 $(a+x) r^{2}+a x(a+x)$ 得 $-\lambda x(a+b)(a+b+c)=-\lambda(a+x) b(b+c)$．因此，$x(a+b)(a+b+c)=(a+x) b(b+c)$，故
$x=\dfrac{a b(b+c)}{(a+b)(a+b+c)-b(b+c)}=\dfrac{b(b+c)}{a+2 b+c},M K \cdot N K-S K \cdot T K=x(a+x)-(b-x)(b+c-x)=x(a+2 b+c)-b(b+c)=0$
因此，$S K \cdot T K=M K \cdot N K=Q K \cdot R K$，故 $Q、R、S、T$ 四点共圆．
证法二
首先 $\angle D T M=\angle E N M-\angle N A T=\angle E M N-\angle M B S=\angle C S N$，故 $\angle F S T=\angle C S N=\angle D T M=\angle F T S$，因此 $F S=F T$．由正弦定理知
$\dfrac{A T}{A N}=\dfrac{\sin \angle A N T}{\sin \angle A^{\prime} T^{\prime} N}, \dfrac{B S}{B M}=\dfrac{\sin \angle B M S}{\sin \angle B S M}$
$\dfrac{C S}{C N}=\dfrac{\sin \angle C N S}{\sin \angle C S N}, \dfrac{D T}{D M}=\dfrac{\sin \angle D M T}{\sin \angle D T M}$ ①
由于 $\angle A T N=\angle D T M=\angle C S N=\angle B S M$．又 $180^{\circ}-\angle B M S=\angle D M T=\angle A N M=\angle C N S=180^{\circ}-\angle A N T$，
故 ① 式中每个等式右边的分子和分母均相同，因此 $\dfrac{A T}{A N}=\dfrac{B S}{B M}=\dfrac{C S}{C N}=\dfrac{D T}{D M}$．
设此比值为 $k$．记 $\omega_3$ 为与 $ FS、FT$ 分别切于点 $S、T$ 的圆（由 $FS = FT$ 知此 圆存在）．如图
，设 $\omega_{1}, \omega_{2}, \omega_{3}$ 的圆心分别为 $O_{1}, O_{2}, O_{3}$，半径分别为 $r_1, r_2 , r_3$．对平面上任意一点 $ P$，定义 $f(P)=\left(k^{2}-1\right)\left(P O_{1}^{2}-r_{1}^{2}\right)-k^{2}\left(P\left(O_{2}^{2}-r_{2}^{2}\right)+\left(P O_{3}^{2}-r_{3}^{2}\right)\right.$．那么 $f(A)=\left(k^{2}-1\right) \cdot 0-k^{2} \cdot A N^{2}+A T^{2}=0$，同理 $f(B)=f(C)=f(D)=0$．建立平面直角坐标系，设 $O_i$ 的坐标为 $\left(x_{i}, y_{i}\right)(i=1,2,3)$，则
$ f(x, y)=\left(k^{2}-1\right)\left[\left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}-r_{1}^{2}\right] -k^{2}\left[\left(x-x_{2}\right)^{2}+\left(y-y_{2}\right)^{2}-r_{2}^{2}\right] +\left[\left(x-x_{3}\right)^{2}+\left(y-y_{3}\right)^{2}-r_{3}^{2}\right] = a x+b y+c $（$a,b,c$ 为常数）
若 $a、b、c$ 不全为零，则满足 $f(x, y) = 0$ 的点 $(x, y)$（若存在）的轨迹是 一条直线，但此直线须过 $A,B,C,D $ 四个点，矛盾！因此 $a = b=c = d = 0$，即 $f$ 恒为 $ 0$．由 $RO_1^2 = r_1^2, RO_2^2= r_2^2$ 及 $f(R)= 0$ 知 $RO_3^2 = r_3^2$．即 $ R $ 在 $\omega_3$ 上．同理，$ Q $ 在 $ \omega_3 $ 上．因此 $ Q、R、S、T $ 四点共圆 $ \omega_3$．
答案
解析
备注
