如图,已知椭圆 $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0)$ 上 $A$、$B$ 两点的切线垂直交于点 $P$,$F_{1}$、$F_{2}$ 是该椭圆的两个焦点。
$(1)$ 当点 $A$、$B$ 在椭圆上运动时,试求动点 $P$ 的轨迹 $E$ 的方程。
$(2)$ 当 $P$ 为曲线 $E$ 上任意一点,证明:$\overrightarrow{P F}_{1} \cdot \overrightarrow{P F}_{2}$ 为定值。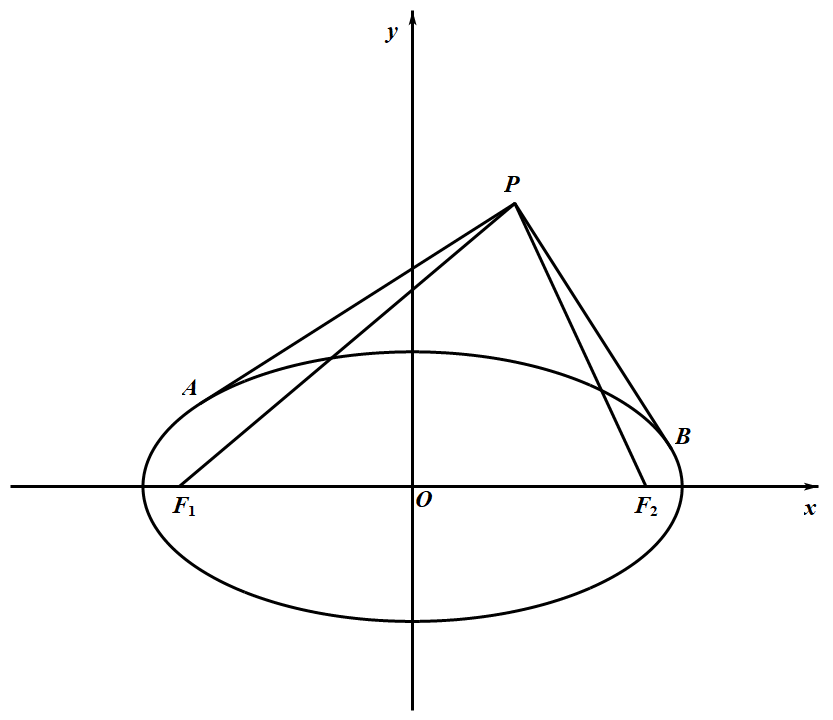
$(1)$ 当点 $A$、$B$ 在椭圆上运动时,试求动点 $P$ 的轨迹 $E$ 的方程。
$(2)$ 当 $P$ 为曲线 $E$ 上任意一点,证明:$\overrightarrow{P F}_{1} \cdot \overrightarrow{P F}_{2}$ 为定值。

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注