如图,在 $\triangle ABC$ 中,$P$、$Q$ 分别为边 $AB$、$AC$ 上的点,且 $AP=AQ$;$R$、$S$ 均在边 $BC$ 上,且 $\angle RPB = \angle PSR, \angle SPQ = \angle SQC$,线段 $PS$ 与 $RQ$ 交于点 $D$;过 $D$ 点分别作 $PR$、$QS$ 的平行线,分别与 $AB$、$AC$ 交于点 $M$、$N$,与 $BC$ 交于点 $F$、$E$ 。证明:$M$、$N$、$F$、$E$ 四点共圆。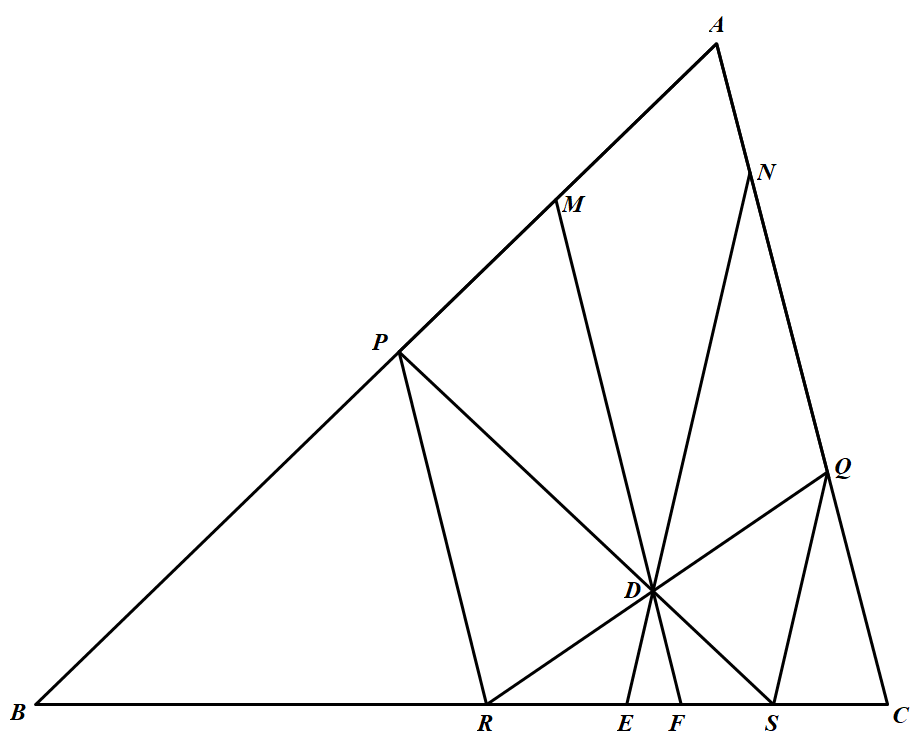

【难度】
【出处】
无
【标注】
【答案】
中等数学 2017_8_3
【解析】
略
答案
解析
备注