如图,已知 $A$、$B$ 分别为椭圆 $\dfrac{x^{2}}{r^{2}}+y^{2}=1(r>0)$ 的左、右顶点,$P A \perp A B$,$M B \perp A B$ 。过点 $P$ 作椭圆的切线,切点为异于点 $A$ 的点 $F$,过点 $M$ 作椭圆的切线,切点为异于点 $B$ 的点 $E$ 。 $AE$ 与 $BF$ 交于点 $C$ 。证明:$P$、$C$、$M$ 三点共线。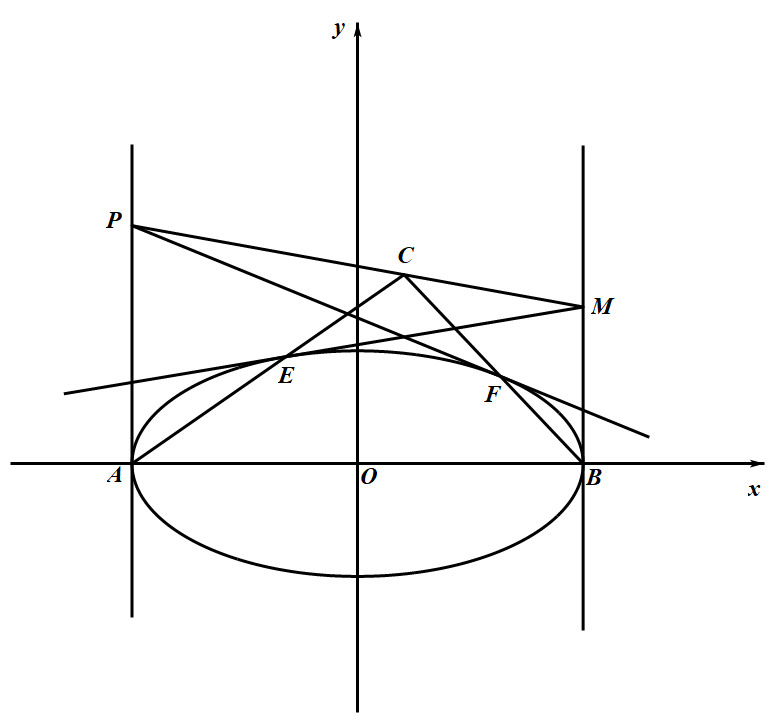

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注