如图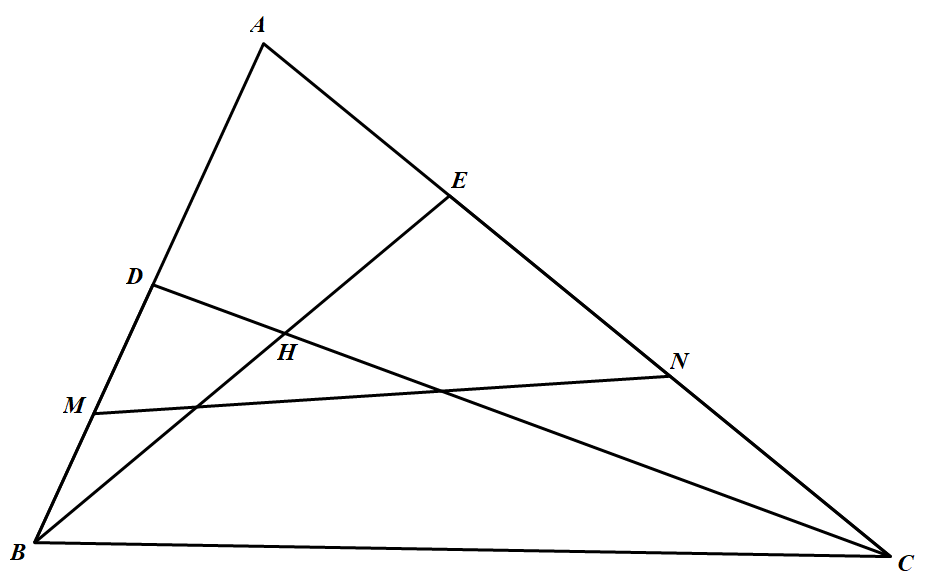 在锐角 $\triangle ABC$ 中,点 $DE$ 分别在边 $AB,AC$ 上,线段 $BE,DC$ 交于点 $H$,点 $M、N$ 分别为线段 $BD、CE$ 的中点.
在锐角 $\triangle ABC$ 中,点 $DE$ 分别在边 $AB,AC$ 上,线段 $BE,DC$ 交于点 $H$,点 $M、N$ 分别为线段 $BD、CE$ 的中点.
证明:点 $H$ 为 $\triangle AMN$ 的垂心的充要条件是 $B,C,E,D$ 四点共圆且 $BE$ 上 $CD$.
 在锐角 $\triangle ABC$ 中,点 $DE$ 分别在边 $AB,AC$ 上,线段 $BE,DC$ 交于点 $H$,点 $M、N$ 分别为线段 $BD、CE$ 的中点.
在锐角 $\triangle ABC$ 中,点 $DE$ 分别在边 $AB,AC$ 上,线段 $BE,DC$ 交于点 $H$,点 $M、N$ 分别为线段 $BD、CE$ 的中点.证明:点 $H$ 为 $\triangle AMN$ 的垂心的充要条件是 $B,C,E,D$ 四点共圆且 $BE$ 上 $CD$.
【难度】
【出处】
2017年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
如图 延长 $MH$ 交 $AC$ 于点 $P$,延长 $NH$ 交 $AB$ 于点 $Q$.
延长 $MH$ 交 $AC$ 于点 $P$,延长 $NH$ 交 $AB$ 于点 $Q$.
先证充分性:由于 $B,C,E,D$ 四点共圆,故 $\angle B D H=\angle C E H$.又 $BE\bot CD$,从而 $\triangle DHB,\triangle EHC$ 均为直角三角形,注意到点 $M,N$ 分别为斜边 $B D, C E$ 的中点,故 $\angle M D H=\angle M H D$,$\angle M H B=\angle M B H$,从而 $\begin{aligned} \angle E H P+\angle H E C &=\angle M H B+\angle H D B =\angle M B H+\angle H D B=90^{\circ} \end{aligned}$
即 $MH\bot AC$.同理 $NH\bot AB$,从而点 $H$ 为 $\triangle AMN$ 的垂心.
再证必要性:若点 $H$ 为 $\triangle AMN$ 的垂心,则 $MP\bot AN, NQ\bot AM$,从而 $\dfrac{D Q}{Q B}=\dfrac{D H \cdot \sin \angle D H Q}{B H \cdot \sin \angle B H Q}=\dfrac{D H \cdot \sin \angle C H N}{B H \cdot \sin \angle E H N}=\dfrac{D H \cdot E H}{B H \cdot C H}$.
同理 $\dfrac{E P}{P C}=\dfrac{D H \cdot E H}{B H \cdot C H}$,故 $\dfrac{E P}{P C}=\dfrac{D Q}{Q B}$.利用比例性质及 $D M=M B, E N=NC$,可知 $\dfrac{E C}{P C}=\dfrac{D B}{Q B} \Rightarrow \dfrac{N C}{P C}=\dfrac{M B}{Q B} \Rightarrow \dfrac{N C}{P N}=\dfrac{M B}{Q M} \Rightarrow \dfrac{E N}{P N}=\dfrac{D M}{Q M}$
又因为点 $H$ 为 $\triangle AMN$ 的垂心,故 $\angle DMH=\angle ENH$,从而有 $\dfrac{Q M}{M H}=\dfrac{P N}{N H}$,因此 $\dfrac{D M}{M H}=\dfrac{E N}{N H}$,从而 $\triangle D M H \sim \triangle E N H$,故 $\angle M D H=\angle N E H$,因此 $B,C,E,D$ 四点共圆.
设四边形 $BCED$ 的外心为 $ O$,易知 $OM\bot AB$,从而 $OM \parallel NH$,同理 $ON\parallel MH$.故四边形 $MHNO$ 为平行四边形,因此 $MH=ON$.过点 $B$ 作 $MH$ 的平行线交 $DC$ 于点 $X$,注意到 $M$ 为 $DB$ 的中点,故 $BX = 2MH = 2ON$,由熟 知的外心性质可知 $X$ 为 $\triangle BCE$ 的垂心,从而 $CX\bot BE$,即 $CD\bot BE$.
 延长 $MH$ 交 $AC$ 于点 $P$,延长 $NH$ 交 $AB$ 于点 $Q$.
延长 $MH$ 交 $AC$ 于点 $P$,延长 $NH$ 交 $AB$ 于点 $Q$.先证充分性:由于 $B,C,E,D$ 四点共圆,故 $\angle B D H=\angle C E H$.又 $BE\bot CD$,从而 $\triangle DHB,\triangle EHC$ 均为直角三角形,注意到点 $M,N$ 分别为斜边 $B D, C E$ 的中点,故 $\angle M D H=\angle M H D$,$\angle M H B=\angle M B H$,从而 $\begin{aligned} \angle E H P+\angle H E C &=\angle M H B+\angle H D B =\angle M B H+\angle H D B=90^{\circ} \end{aligned}$
即 $MH\bot AC$.同理 $NH\bot AB$,从而点 $H$ 为 $\triangle AMN$ 的垂心.
再证必要性:若点 $H$ 为 $\triangle AMN$ 的垂心,则 $MP\bot AN, NQ\bot AM$,从而 $\dfrac{D Q}{Q B}=\dfrac{D H \cdot \sin \angle D H Q}{B H \cdot \sin \angle B H Q}=\dfrac{D H \cdot \sin \angle C H N}{B H \cdot \sin \angle E H N}=\dfrac{D H \cdot E H}{B H \cdot C H}$.
同理 $\dfrac{E P}{P C}=\dfrac{D H \cdot E H}{B H \cdot C H}$,故 $\dfrac{E P}{P C}=\dfrac{D Q}{Q B}$.利用比例性质及 $D M=M B, E N=NC$,可知 $\dfrac{E C}{P C}=\dfrac{D B}{Q B} \Rightarrow \dfrac{N C}{P C}=\dfrac{M B}{Q B} \Rightarrow \dfrac{N C}{P N}=\dfrac{M B}{Q M} \Rightarrow \dfrac{E N}{P N}=\dfrac{D M}{Q M}$
又因为点 $H$ 为 $\triangle AMN$ 的垂心,故 $\angle DMH=\angle ENH$,从而有 $\dfrac{Q M}{M H}=\dfrac{P N}{N H}$,因此 $\dfrac{D M}{M H}=\dfrac{E N}{N H}$,从而 $\triangle D M H \sim \triangle E N H$,故 $\angle M D H=\angle N E H$,因此 $B,C,E,D$ 四点共圆.
设四边形 $BCED$ 的外心为 $ O$,易知 $OM\bot AB$,从而 $OM \parallel NH$,同理 $ON\parallel MH$.故四边形 $MHNO$ 为平行四边形,因此 $MH=ON$.过点 $B$ 作 $MH$ 的平行线交 $DC$ 于点 $X$,注意到 $M$ 为 $DB$ 的中点,故 $BX = 2MH = 2ON$,由熟 知的外心性质可知 $X$ 为 $\triangle BCE$ 的垂心,从而 $CX\bot BE$,即 $CD\bot BE$.
答案
解析
备注