2016IMO Short List

若 $n$ 为偶数，则可以选取的对角线的数目的最大值为 $n-2$；若 $n$ 为奇数，则可以选取的对角线的数目的最大值为 $n-3$．
（1）若 $n$ 为奇数，则不存在两条对角线互相垂直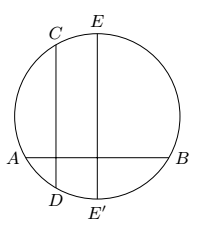．由于 $EC=E'D$，且 $C,D,E$ 均为正 $n$ 边形的顶点，则 $E'$ 也应为正 $n$ 边形的顶点．这与正 $n$ 边形的所有奇数个顶点中不存在其外接圆上的一对对径点矛盾．于是，只需考虑对角线不相交的情况．
选取的对角线的数目达到最大值时选取的对角线应该将正 $n$ 边形分成 $n-2$ 个三角形．从而，最多可以选取 $n-3$ 条对角线，这个最大值是能够取到的．例如，考虑从一个顶点引出的所有对角线共有 $n-3$ 条，且满足条件，如图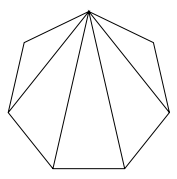．（2）若 $n$ 为偶数，如果选取的对角线中任意两条均不相交，则由（1），知选取的对角线的数目的最大值为 $n-3$．
假设存在两条选取的对角线互相垂直．考虑选取的对角线中与这两条对角线之一平行且与某条选取的对角线相交的对角线的集合为 $S$．假设 $S$ 中包含 $k$ 条对角线，且这 $k$ 条对角线包含的不同端点的个数为 $l$．
首先，考虑在集合 $S$ 中两个方向之一的对角线中最长的一条．则 $S$ 中其他对角线均不是由这条对角线的端点引出的．否则，这条由最长对角线的端点引出的对角线就会与 $S$ 中的一条更长的对角线相交（如图），矛盾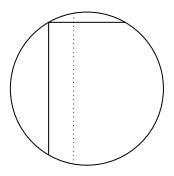．类似地，对另一个方向，可得同样结论．
去掉这两条最长的对角线和其四个端点，剩下 $k-2$ 条对角线和 $l-4$ 个端点，且每个端点最多属于两条对角线．则$$2(l-4)\geqslant 2(k-2)~\Rightarrow ~k\leqslant l-2$$其次，考虑正 $n$ 边形相邻顶点构成的点集，使得两个边界上的顶点中的每一个均为集合 $S$ 中的一条对角线的一个端点，且其内部的点均不为 $S$ 中的对角线的端点．则有 $l$ 个这样的点集，并依次设这些点集为 $P_1 , P_2 ,\ldots , P_l$．
接下来证明：选取的每条不在集合 $S$ 中的对角线一定是同一个点集 $P_i$ 中的两个顶点所连的线段．
假设存在选取的对角线 $d$ 不在集合 $S$ 中，且其两个端点分别在不同的点集 $P_i , P_j$ 中．设 $d_1 , d_2$ 为集合 $S$ 中的两条对角线，且每一条均有一个端点为 $P_i$ 的边界上的点之一．则 $d$ 要么与 $d_1$ 或 $d_2$ 相交，要么与 $S$ 中的一条与 $d_1 , d_2$ 均垂直的对角线相交，如下面的两幅图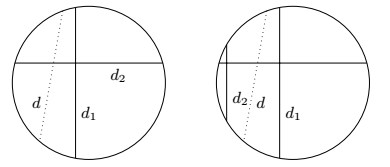．由集合 $S$ 的定义，知 $d\in S$，矛盾．
在同一个点集 $P_i$ 中，由于顶点属于正 $n$ 边形外接圆直径的同一侧，则没有互相垂直的对角线．故在 $P_i$ 中最多可以选取 $|P_i |-2$ 条对角线，其中，当 $|P_i |>2$ 时，包含连接 $P_i$ 的两个边界上的顶点得到的对角线．
因此，选取的对角线的数目的最大值为$$\begin{aligned}&\sum_{i=1}^{l}\left(\left|P_{i}\right|-2\right)+k=\sum_{i=1}^{l}\left|P_{i}\right|-2 l+k \\=&(n+l)-2 l+k=n-l+k \\ \leqslant &n-2\end{aligned}$$下面的例子说明此上界是能够取到的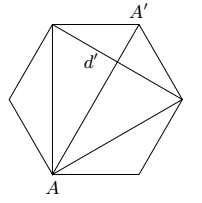．如图，对于正 $n$ 边形的任意一个顶点 $A$，设 $A'$ 为正 $n$ 边形上的另一个点，使得 $AA'$ 为正 $n$ 边形外接圆的直径．选取所有由点 $A$ 引出的对角线及对角线 $d'$，其中，$d'$ 为连接与 $A'$ 相邻的两个顶点的对角线．则只有一条对角线 $AA'$ 和 $d'$ 相交，且互相垂直，这些对角线共有 $n-2$ 条．
因此，可选取的对角线的数目的最大值为 $n-2$ 条

略