如图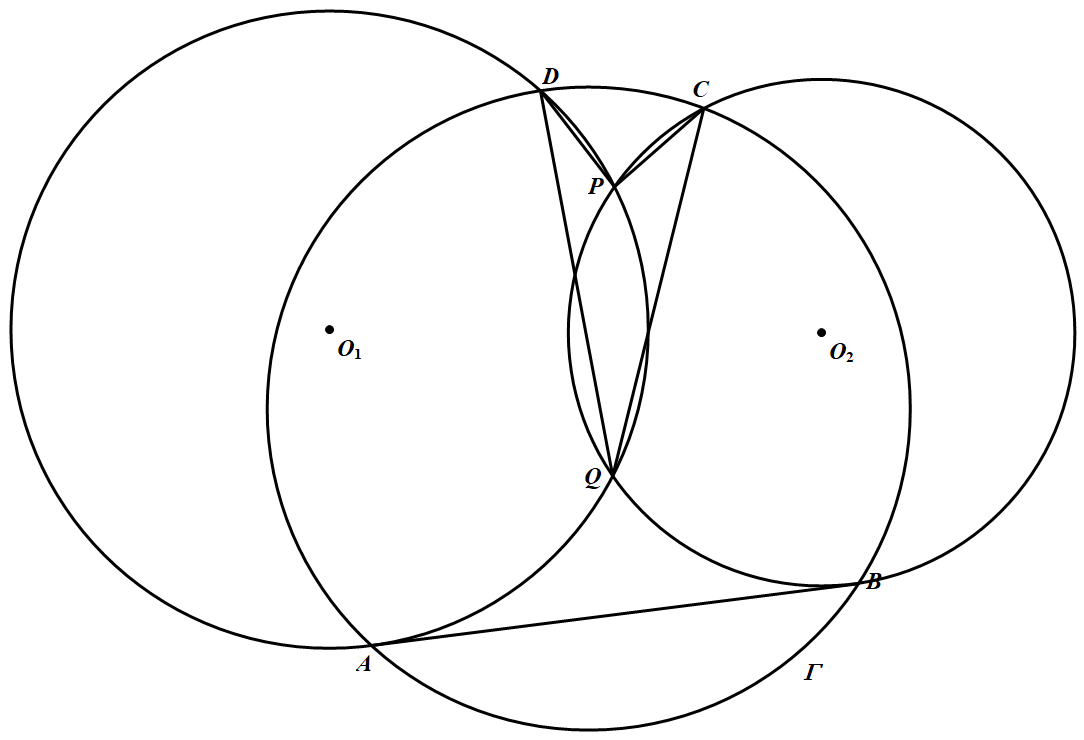
设 $\odot O_1$ 与 $\odot O_2$ 相交于点 $P、Q$．它们的一条外公切线分别切 $\odot O_1,\odot O_2$ 于点 $A、B$，过点 $A、B$ 的圆 $\Gamma$ 分别交 $\odot O_1,\odot O_2$ 于点 $D、C$．证明：$\dfrac{C P}{C Q}=\dfrac{D P}{D Q}$．
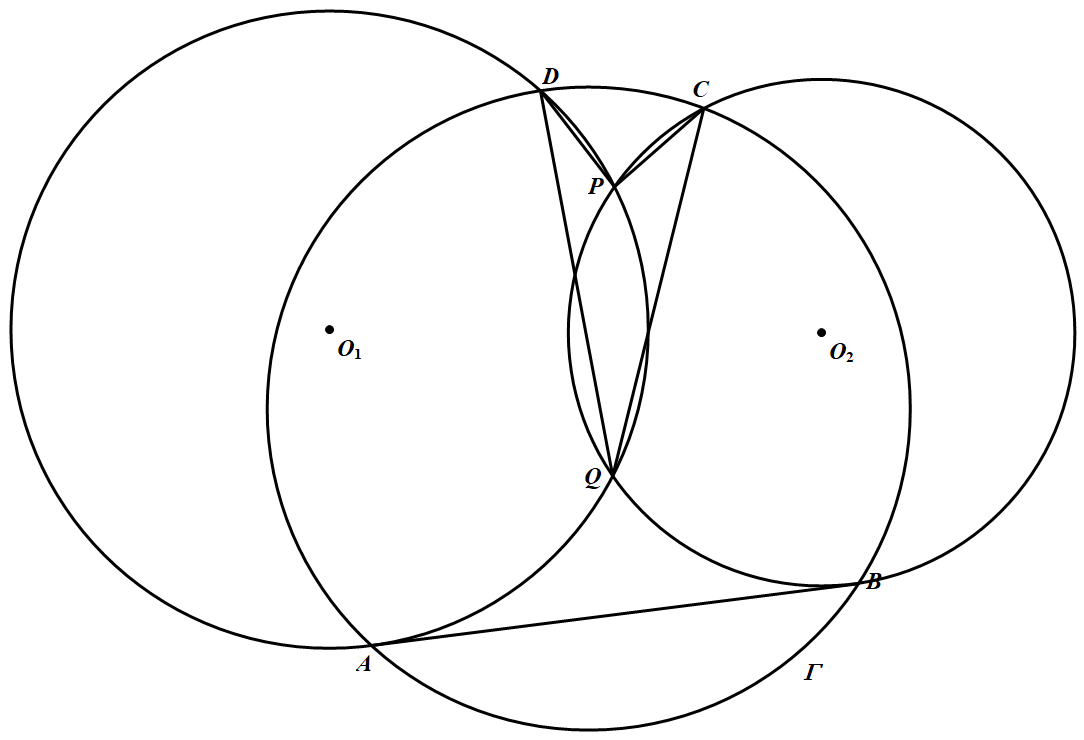设 $\odot O_1$ 与 $\odot O_2$ 相交于点 $P、Q$．它们的一条外公切线分别切 $\odot O_1,\odot O_2$ 于点 $A、B$，过点 $A、B$ 的圆 $\Gamma$ 分别交 $\odot O_1,\odot O_2$ 于点 $D、C$．证明：$\dfrac{C P}{C Q}=\dfrac{D P}{D Q}$．【难度】
【出处】
2016年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
由蒙日定理，直线 $AD、QP、BC$ 交于一点，设为 $K$．连结 $AP、AQ、BP、BQ$．如图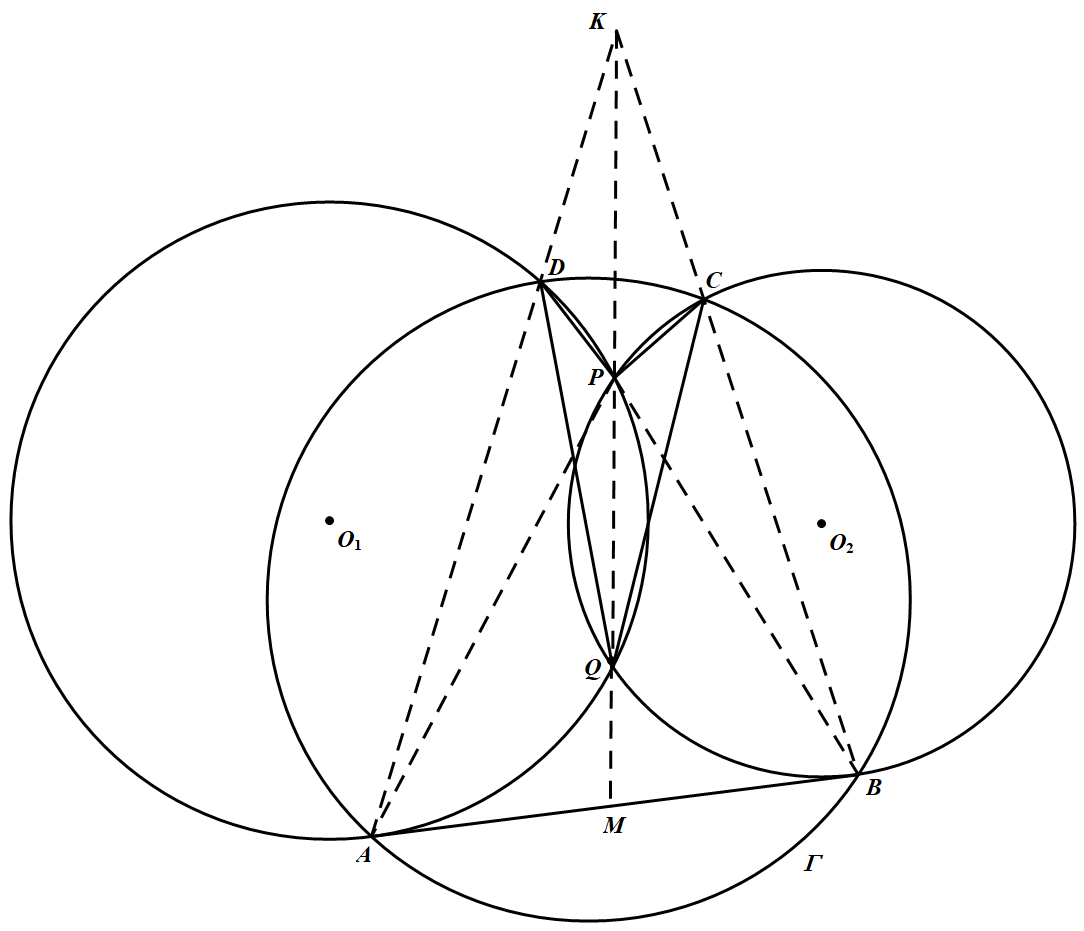
因为 $\triangle K P D \sim \triangle K A Q$，所以 $\dfrac{D P}{A Q}=\dfrac{K P}{K A}$．
因为 $\triangle K P A \sim \triangle K D Q$，所以 $\dfrac{A P}{D Q}=\dfrac{K A}{K Q}$．将两式相乘得，$\dfrac{A P \cdot D P}{A Q \cdot D Q}=\dfrac{K P}{K Q}$．
同理，$\dfrac{B P \cdot C P}{B Q \cdot C Q}=\dfrac{K P}{K Q}$．从而 $\dfrac{A P \cdot D P}{A Q \cdot D Q}=\dfrac{B P \cdot C P}{B Q \cdot C Q}$．①
延长 $PQ$ 交 $AB$ 于点 $M$．因为 $\triangle AQM\sim\triangle PAM$，所以 $\dfrac{A Q}{A P}=\dfrac{A M}{P M}=\dfrac{Q M}{A M}$
于是 $\left(\dfrac{A Q}{A P}\right)^{2}=\dfrac{A M}{P M} \cdot \dfrac{Q M}{A M}=\dfrac{Q M}{P M}$
同理，$\left(\dfrac{B Q}{B P}\right)^{2}=\dfrac{Q M}{P M}$，从而
$\begin{aligned}\left(\dfrac{A Q}{A P}\right)^{2} =\left(\dfrac{B Q}{B P}\right)^{2} , \dfrac{A Q}{A P} =\dfrac{B Q}{B P} \end{aligned}$ ②
由式 ①、② 知，$\dfrac{C P}{C Q}=\dfrac{D P}{D Q}$．
因为 $\triangle K P D \sim \triangle K A Q$，所以 $\dfrac{D P}{A Q}=\dfrac{K P}{K A}$．因为 $\triangle K P A \sim \triangle K D Q$，所以 $\dfrac{A P}{D Q}=\dfrac{K A}{K Q}$．将两式相乘得，$\dfrac{A P \cdot D P}{A Q \cdot D Q}=\dfrac{K P}{K Q}$．
同理，$\dfrac{B P \cdot C P}{B Q \cdot C Q}=\dfrac{K P}{K Q}$．从而 $\dfrac{A P \cdot D P}{A Q \cdot D Q}=\dfrac{B P \cdot C P}{B Q \cdot C Q}$．①
延长 $PQ$ 交 $AB$ 于点 $M$．因为 $\triangle AQM\sim\triangle PAM$，所以 $\dfrac{A Q}{A P}=\dfrac{A M}{P M}=\dfrac{Q M}{A M}$
于是 $\left(\dfrac{A Q}{A P}\right)^{2}=\dfrac{A M}{P M} \cdot \dfrac{Q M}{A M}=\dfrac{Q M}{P M}$
同理，$\left(\dfrac{B Q}{B P}\right)^{2}=\dfrac{Q M}{P M}$，从而
$\begin{aligned}\left(\dfrac{A Q}{A P}\right)^{2} =\left(\dfrac{B Q}{B P}\right)^{2} , \dfrac{A Q}{A P} =\dfrac{B Q}{B P} \end{aligned}$ ②
由式 ①、② 知，$\dfrac{C P}{C Q}=\dfrac{D P}{D Q}$．
答案
解析
备注
