如图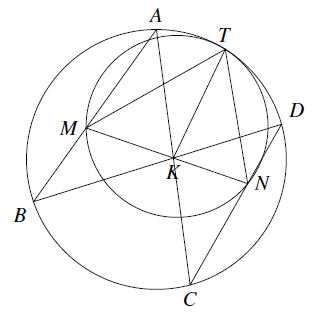
圆 $\omega_1$ 与圆 $\omega_2$ 内切于点 $T$．$M,N$ 是圆 $\omega_1$ 上不同于 $T$ 的不同两点．圆 $\omega_2$ 的两条弦 $AB,CD$ 分别过 $M,N$．
证明：若线段 $AC,BD,MN$ 交于同一点 $K$．求证：$TK$ 平分 $\angle MTN$．
圆 $\omega_1$ 与圆 $\omega_2$ 内切于点 $T$．$M,N$ 是圆 $\omega_1$ 上不同于 $T$ 的不同两点．圆 $\omega_2$ 的两条弦 $AB,CD$ 分别过 $M,N$．证明：若线段 $AC,BD,MN$ 交于同一点 $K$．求证：$TK$ 平分 $\angle MTN$．
【难度】
【出处】
2015年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
如图
分别延长 $TM,TN$ 交圆 $\omega_2$ 于点 $E,F$．连结 $EF$，从而 $MN\parallel EF$．于是 $\dfrac{TM}{TN}=\dfrac{ME}{NF}$
故 $\dfrac{T M^{2}}{T N^{2}}=\dfrac{T M}{T N} \cdot \dfrac{M E}{N F}=\dfrac{A M \cdot M B}{D N \cdot N C}$ ①（这里用到相交弦定理）
在 $\triangle AMK$ 和 $\triangle DNK$ 中，由正弦定理知 $\dfrac{A M}{\sin \angle A K M}=\dfrac{M K}{\sin \angle M A K}, \dfrac{D N}{\sin \angle D K N}=\dfrac{K N}{\sin \angle K D N}$
注意到 $\angle M A K=\angle B A C=\angle B D C=\angle K D N$，
于是 $\dfrac{A M}{D N}=\dfrac{M K \cdot \sin \angle A K M}{N K \cdot \sin \angle D K N}$
同理可知 $\dfrac{M B}{N C}=\dfrac{M K \cdot \sin \angle M K B}{N K \cdot \sin \angle N K C}$
从而 $\dfrac{A M \cdot M B}{D N \cdot N C}=\dfrac{M K^{2}}{N K^{2}}$ ②
由 ①，② 知 $
\dfrac{T M^{2}}{T N^{2}}=\dfrac{M K^{2}}{N K^{2}}
$ 即 $
\dfrac{T M}{T N}=\dfrac{M K}{N K}
$
故 $ TK $ 平分 $ \angle MTN$．
分别延长 $TM,TN$ 交圆 $\omega_2$ 于点 $E,F$．连结 $EF$，从而 $MN\parallel EF$．于是 $\dfrac{TM}{TN}=\dfrac{ME}{NF}$故 $\dfrac{T M^{2}}{T N^{2}}=\dfrac{T M}{T N} \cdot \dfrac{M E}{N F}=\dfrac{A M \cdot M B}{D N \cdot N C}$ ①（这里用到相交弦定理）
在 $\triangle AMK$ 和 $\triangle DNK$ 中，由正弦定理知 $\dfrac{A M}{\sin \angle A K M}=\dfrac{M K}{\sin \angle M A K}, \dfrac{D N}{\sin \angle D K N}=\dfrac{K N}{\sin \angle K D N}$
注意到 $\angle M A K=\angle B A C=\angle B D C=\angle K D N$，
于是 $\dfrac{A M}{D N}=\dfrac{M K \cdot \sin \angle A K M}{N K \cdot \sin \angle D K N}$
同理可知 $\dfrac{M B}{N C}=\dfrac{M K \cdot \sin \angle M K B}{N K \cdot \sin \angle N K C}$
从而 $\dfrac{A M \cdot M B}{D N \cdot N C}=\dfrac{M K^{2}}{N K^{2}}$ ②
由 ①，② 知 $
\dfrac{T M^{2}}{T N^{2}}=\dfrac{M K^{2}}{N K^{2}}
$ 即 $
\dfrac{T M}{T N}=\dfrac{M K}{N K}
$
故 $ TK $ 平分 $ \angle MTN$．
答案
解析
备注
