如图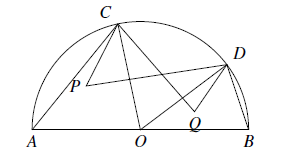
$AB$ 是半圆 $O$ 的直径，$C,D$ 是 $AB$ 上两点，$P,Q$ 分别是 $\triangle OAC$ 与 $\triangle OBD$ 的外心．证明：$CP\cdot CQ=DP\cdot DQ$．
$AB$ 是半圆 $O$ 的直径，$C,D$ 是 $AB$ 上两点，$P,Q$ 分别是 $\triangle OAC$ 与 $\triangle OBD$ 的外心．证明：$CP\cdot CQ=DP\cdot DQ$．【难度】
【出处】
2014年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
连结 $OP,OQ,AP,AD,BQ,BC$．设 $\angle BAD=\alpha$，$\angle ABC=\beta$．
由条件得，
$\begin{aligned}
&\angle OAP=\angle AOP=\frac{1}{2}\angle AOC=\angle ABC=\beta\\ &\angle OBQ=\angle BOQ=\frac{1}{2}\angle BOD=\angle BAD=\alpha
\end{aligned}$
故 $\angle PAD=\angle OAP-\angle OAD=\beta-\alpha=\angle OBC-\angle OBQ=\angle QBC$．
又 $
\dfrac{A D}{A P}=\dfrac{A D}{A B} \cdot \dfrac{A B}{A O} \cdot \dfrac{A O}{A P}=\cos \alpha \cdot 2 \cdot 2 \cos \beta=4 \cos \alpha \cos \beta
$
同理得，$\dfrac{B C}{B Q}=4 \cos \beta \cos \alpha$，
所以 $\dfrac{AD}{AP}=\dfrac{BC}{BQ}$，
从而 $\triangle APD\sim\triangle BQC$，
得 $\dfrac{AP}{DP}=\dfrac{BQ}{CQ}$，
于是有 $CP\cdot CQ=AP\cdot CQ=DP\cdot BQ=DP\cdot DQ$
由条件得，
$\begin{aligned}
&\angle OAP=\angle AOP=\frac{1}{2}\angle AOC=\angle ABC=\beta\\ &\angle OBQ=\angle BOQ=\frac{1}{2}\angle BOD=\angle BAD=\alpha
\end{aligned}$
故 $\angle PAD=\angle OAP-\angle OAD=\beta-\alpha=\angle OBC-\angle OBQ=\angle QBC$．
又 $
\dfrac{A D}{A P}=\dfrac{A D}{A B} \cdot \dfrac{A B}{A O} \cdot \dfrac{A O}{A P}=\cos \alpha \cdot 2 \cdot 2 \cos \beta=4 \cos \alpha \cos \beta
$
同理得，$\dfrac{B C}{B Q}=4 \cos \beta \cos \alpha$，
所以 $\dfrac{AD}{AP}=\dfrac{BC}{BQ}$，
从而 $\triangle APD\sim\triangle BQC$，
得 $\dfrac{AP}{DP}=\dfrac{BQ}{CQ}$，
于是有 $CP\cdot CQ=AP\cdot CQ=DP\cdot BQ=DP\cdot DQ$
答案
解析
备注
