平面上，点 $O$ 是正三角形 $ABC$ 的中心，点 $P,Q$ 满足 $\overrightarrow{OQ}=2\overrightarrow{PO}$．
证明：$|P A|+|P B|+|P C| \leqslant|Q A|+|Q B|+|Q C|$
证明：$|P A|+|P B|+|P C| \leqslant|Q A|+|Q B|+|Q C|$
【难度】
【出处】
2014年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
证法一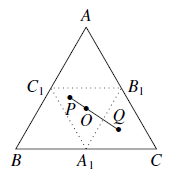
设 $BC,CA,AB$ 的中点分别为 $A_1 , B_1 , C_1$．由于 $\triangle ABC$ 与 $\triangle A_1 B_1 C_1$ 关于点 $O$ 位似，
位似比为 $1:(-2)$，故在此变换下，$P\rightarrow Q$，
从而 $QA+QB+QC=2(PA_1 + PB_1 + PC_1 )$
在四边形 $PA_1 BC_1$ 中，由托勒密不等式，
有 $
P B \cdot A_{1} C_{1} \leqslant P C_{1} \cdot A_{1} B+P A_{1} \cdot B C_{1}
$
注意到 $\triangle A_1 B C_1$ 为正三角形，则 $PB\leqslant PA_1 +PC_1$．
同理，$PC\leqslant PA_1 +PB_1$，$PA\leqslant PB_1 +PC_1$，以上三式相加，
有 $PA+PB+PC\leqslant 2(PA_1 + PB_1 + PC_1 )$
故 $ PA+PB+PC\leqslant QA+QB+QC $．
证法二
只需证明，$ QA+QB\geqslant 2PC $．我们记 $ \omega =e^{i\frac{2\pi}{3}} $，则 $ \overrightarrow{OB}=\omega\overrightarrow{OA},\overrightarrow{OC}=\omega^2 \overrightarrow{OA},\overrightarrow{OQ}=-2\overrightarrow{OP} $，
从而
$ \begin{aligned}&QA+QB\geqslant 2PC \\ \Leftrightarrow &|\overrightarrow{OA}-\overrightarrow{OQ}|+|\overrightarrow{OB}-\overrightarrow{OQ}|\geqslant 2|\overrightarrow{OC}-\overrightarrow{OP}|\\ \Leftrightarrow & |\overrightarrow{OA}+2\overrightarrow{OP}|+|\omega\overrightarrow{OA}+2\overrightarrow{OP}|\geqslant 2|\omega^2 \overrightarrow{OA}-\overrightarrow{OP}|\\ \Leftrightarrow &|\overrightarrow{OA}+2\overrightarrow{OP}|+|\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|\geqslant 2|\overrightarrow{OA}-\omega\overrightarrow{OP}|\end{aligned} $
事实上，由三角形不等式，
$ \begin{aligned}\overrightarrow{OA}+2\overrightarrow{OP}|+|\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|&\geqslant \overrightarrow{OA}+2\overrightarrow{OP}+\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|=2|\overrightarrow{OA}+(1+\omega^2 )\overrightarrow{OP}| =2|\overrightarrow{OA}-\omega\overrightarrow{OP}|\end{aligned} $
故 $ QA+QB\geqslant 2PC $，同理还有 $ QB+QC\geqslant 2PA $，
$ QC+QA\geqslant 2PB $，三式相加即为 $ PA+PB+PC\leqslant QA+QB+QC $
设 $BC,CA,AB$ 的中点分别为 $A_1 , B_1 , C_1$．由于 $\triangle ABC$ 与 $\triangle A_1 B_1 C_1$ 关于点 $O$ 位似，位似比为 $1:(-2)$，故在此变换下，$P\rightarrow Q$，
从而 $QA+QB+QC=2(PA_1 + PB_1 + PC_1 )$
在四边形 $PA_1 BC_1$ 中，由托勒密不等式，
有 $
P B \cdot A_{1} C_{1} \leqslant P C_{1} \cdot A_{1} B+P A_{1} \cdot B C_{1}
$
注意到 $\triangle A_1 B C_1$ 为正三角形，则 $PB\leqslant PA_1 +PC_1$．
同理，$PC\leqslant PA_1 +PB_1$，$PA\leqslant PB_1 +PC_1$，以上三式相加，
有 $PA+PB+PC\leqslant 2(PA_1 + PB_1 + PC_1 )$
故 $ PA+PB+PC\leqslant QA+QB+QC $．
证法二
只需证明，$ QA+QB\geqslant 2PC $．我们记 $ \omega =e^{i\frac{2\pi}{3}} $，则 $ \overrightarrow{OB}=\omega\overrightarrow{OA},\overrightarrow{OC}=\omega^2 \overrightarrow{OA},\overrightarrow{OQ}=-2\overrightarrow{OP} $，
从而
$ \begin{aligned}&QA+QB\geqslant 2PC \\ \Leftrightarrow &|\overrightarrow{OA}-\overrightarrow{OQ}|+|\overrightarrow{OB}-\overrightarrow{OQ}|\geqslant 2|\overrightarrow{OC}-\overrightarrow{OP}|\\ \Leftrightarrow & |\overrightarrow{OA}+2\overrightarrow{OP}|+|\omega\overrightarrow{OA}+2\overrightarrow{OP}|\geqslant 2|\omega^2 \overrightarrow{OA}-\overrightarrow{OP}|\\ \Leftrightarrow &|\overrightarrow{OA}+2\overrightarrow{OP}|+|\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|\geqslant 2|\overrightarrow{OA}-\omega\overrightarrow{OP}|\end{aligned} $
事实上，由三角形不等式，
$ \begin{aligned}\overrightarrow{OA}+2\overrightarrow{OP}|+|\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|&\geqslant \overrightarrow{OA}+2\overrightarrow{OP}+\overrightarrow{OA}+2\omega^2 \overrightarrow{OP}|=2|\overrightarrow{OA}+(1+\omega^2 )\overrightarrow{OP}| =2|\overrightarrow{OA}-\omega\overrightarrow{OP}|\end{aligned} $
故 $ QA+QB\geqslant 2PC $，同理还有 $ QB+QC\geqslant 2PA $，
$ QC+QA\geqslant 2PB $，三式相加即为 $ PA+PB+PC\leqslant QA+QB+QC $
答案
解析
备注
