如图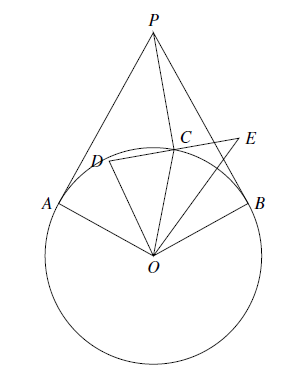
$PA,PB$ 为圆 $O$ 的切线，点 $C$ 在劣弧 $\overparen{AB}$ 上（不含点 $A,B$）．过点 $C$ 作 $PC$ 的垂线 $l$，与 $\angle AOC$ 的平分线交于点 $D$，与 $\angle BOC$ 的平分线交于点 $E$．求证：$CD=CE$．
$PA,PB$ 为圆 $O$ 的切线，点 $C$ 在劣弧 $\overparen{AB}$ 上（不含点 $A,B$）．过点 $C$ 作 $PC$ 的垂线 $l$，与 $\angle AOC$ 的平分线交于点 $D$，与 $\angle BOC$ 的平分线交于点 $E$．求证：$CD=CE$．【难度】
【出处】
2013年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
证法一
由于 $C$ 不与 $A$ 重合，且 $PC \perp CD$，$PA\perp AO$ 故 $CD$ 与 $AO$ 不平行．
因此，设直线 $L$ 交 $OA$ 于点 $M$，则 $P,C,A,M$ 四点共圆（图中给出的是点 $M$ 在 $OA$ 延长线上的情况，若 $M$ 与 $A$ 重合或在线段 $OA$ 内，则完全类似）．
所以 $\angle A P C=\angle A M C$ ①
连结 $AC$，则
$\angle P A C=\dfrac{1}{2} \angle A O C=\angle M O D$ ②
由 ①，② 得 $\triangle PAC\sim\triangle MOD$，
从而 $\dfrac{P C}{P A}=\dfrac{M D}{M O}$，注意到 $OD$ 平分 $\angle AOC$，故由角平分线定理可得 $
\dfrac{C D}{C O}=\dfrac{M D}{M O}=\dfrac{P C}{P A}
$
另一方面，同理可知 $\dfrac{C E}{C O}=\dfrac{P C}{P B}$，而 $PA=PB$，所以 $CD=CE$．
证法二
设直线 $PC$ 与圆 $O$ 交于点 $C$ 与另一点 $F$．连结 $BC, BE,BF, OF$，如图
由于 $B,C$ 在圆 $O$ 上，$OE$ 平分 $\angle BOC$，故 $OE$ 垂直平分 $BC$，
所以 $CE=BE$．又 $FO=BO$，$PC\perp DE$，得 $\begin{aligned} \angle C E B &=2\left(90^{\circ}-\angle E C B\right) =2 \angle B C F=\angle B O F \end{aligned}$
所以 $\triangle CEB\sim\triangle BOF$，从而 $
\dfrac{C E}{B O}=\dfrac{C B}{B F}
$ ①
由 $PB$ 是圆 $O$ 切线知 $\angle PBC=\angle PFB$，故 $\triangle PCB\sim\triangle PBF$，所以 $
\dfrac{C B}{B F}=\dfrac{P C}{P B}
$ ②
由 ①，② 得 $CE=BO\cdot\dfrac{PC}{PB}$．
由对称性可知 $CD=AO\cdot\dfrac{PC}{PA}$，于是结合 $AO=BO$，$PA=PB$，得 $CD=CE$．
证法三
如图，连结 $AB,AC,BC$，记 $OD$ 与 $AC$ 交于点 $M$．
由于 $A,C$ 在圆 $O$ 上，$OD$ 平分 $\angle AOC$，故 $\angle DMC=90^{\circ}$ 且 $MC=\dfrac{1}{2}AC$．又 $PC\perp DE$，
故 $\cos\angle ACD=\sin\angle ACP$，则
$C D=\dfrac{M C}{\cos \angle A C D}=\dfrac{A C}{2 \sin \angle A C P}
$ ①
记圆 $O$ 半径为 $R$，注意到 $PA$ 为圆 $O$ 的切线，故 $\angle ABC=\angle CAP$．因此，根据 ① 及正弦定理可知 $
C D=\dfrac{2 R \sin \angle A B C}{2 \sin \angle A C P}=R \cdot \dfrac{\sin \angle C A P}{\sin \angle A C P}=R \cdot \dfrac{C P}{A P}
$
由对称性知 $CE=R\cdot\dfrac{CP}{BP}$，于是结合 $AP=BP$，可得 $CD=CE$．
由于 $C$ 不与 $A$ 重合，且 $PC \perp CD$，$PA\perp AO$ 故 $CD$ 与 $AO$ 不平行．
因此，设直线 $L$ 交 $OA$ 于点 $M$，则 $P,C,A,M$ 四点共圆（图中给出的是点 $M$ 在 $OA$ 延长线上的情况，若 $M$ 与 $A$ 重合或在线段 $OA$ 内，则完全类似）．
所以 $\angle A P C=\angle A M C$ ①连结 $AC$，则
$\angle P A C=\dfrac{1}{2} \angle A O C=\angle M O D$ ②
由 ①，② 得 $\triangle PAC\sim\triangle MOD$，
从而 $\dfrac{P C}{P A}=\dfrac{M D}{M O}$，注意到 $OD$ 平分 $\angle AOC$，故由角平分线定理可得 $
\dfrac{C D}{C O}=\dfrac{M D}{M O}=\dfrac{P C}{P A}
$
另一方面，同理可知 $\dfrac{C E}{C O}=\dfrac{P C}{P B}$，而 $PA=PB$，所以 $CD=CE$．
证法二
设直线 $PC$ 与圆 $O$ 交于点 $C$ 与另一点 $F$．连结 $BC, BE,BF, OF$，如图
由于 $B,C$ 在圆 $O$ 上，$OE$ 平分 $\angle BOC$，故 $OE$ 垂直平分 $BC$，所以 $CE=BE$．又 $FO=BO$，$PC\perp DE$，得 $\begin{aligned} \angle C E B &=2\left(90^{\circ}-\angle E C B\right) =2 \angle B C F=\angle B O F \end{aligned}$
所以 $\triangle CEB\sim\triangle BOF$，从而 $
\dfrac{C E}{B O}=\dfrac{C B}{B F}
$ ①
由 $PB$ 是圆 $O$ 切线知 $\angle PBC=\angle PFB$，故 $\triangle PCB\sim\triangle PBF$，所以 $
\dfrac{C B}{B F}=\dfrac{P C}{P B}
$ ②
由 ①，② 得 $CE=BO\cdot\dfrac{PC}{PB}$．
由对称性可知 $CD=AO\cdot\dfrac{PC}{PA}$，于是结合 $AO=BO$，$PA=PB$，得 $CD=CE$．
证法三
如图，连结 $AB,AC,BC$，记 $OD$ 与 $AC$ 交于点 $M$．
由于 $A,C$ 在圆 $O$ 上，$OD$ 平分 $\angle AOC$，故 $\angle DMC=90^{\circ}$ 且 $MC=\dfrac{1}{2}AC$．又 $PC\perp DE$，故 $\cos\angle ACD=\sin\angle ACP$，则
$C D=\dfrac{M C}{\cos \angle A C D}=\dfrac{A C}{2 \sin \angle A C P}
$ ①
记圆 $O$ 半径为 $R$，注意到 $PA$ 为圆 $O$ 的切线，故 $\angle ABC=\angle CAP$．因此，根据 ① 及正弦定理可知 $
C D=\dfrac{2 R \sin \angle A B C}{2 \sin \angle A C P}=R \cdot \dfrac{\sin \angle C A P}{\sin \angle A C P}=R \cdot \dfrac{C P}{A P}
$
由对称性知 $CE=R\cdot\dfrac{CP}{BP}$，于是结合 $AP=BP$，可得 $CD=CE$．
答案
解析
备注
