将一个正 $n$ 边形的 $n$ 条边按顺时针方向依次标上 $1,2,\ldots,n$．求所有的整数 $n\geqslant 4$，使得可以用 $n-3$ 条在内部不交的对角线将这个 $n$ 边形分成 $n-2$ 个三角形区域，并且在这 $n-3$ 条对角线上分别标上一个整数，满足每个三角形的三边所标之数的和都相等．
【难度】
【出处】
2013年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
当 $n\geqslant 4$ 且 $n\not\equiv 2\pmod{4}$ 时满足条件．
首先证明若 $n$ 满足条件，
则 $n\not\equiv 2\pmod{4}$．
若正整数 $n$ 满足条件，设每个三角形三边所标整数之和为 $S$，所有 $n-3$ 条对角线所标整数之和为 $m$，对所有 $n-2$ 个三角形边所标数之和求和，每条对角线都计算了两次，可得 $(n-2)S=(1+2+\ldots+n)+2m$
假设 $n\equiv 2\pmod{4}$，则 $(n-2)S$ 为偶数，而 $(1+2+\ldots+n)+2m$ 为奇数，矛盾．因此 $n\not\equiv 2\pmod{4}$．
以下证明所有 $n\geqslant 4$ 且 $n\not\equiv 2\pmod {4}$ 都满足条件．
如图分别给出了 $n=4,5,7$ 时的构造，可直接验证满足条件．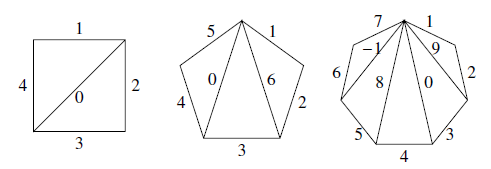
下面用归纳法证明若 $n$ 满足条件，则 $n+4$ 也满足条件．如图
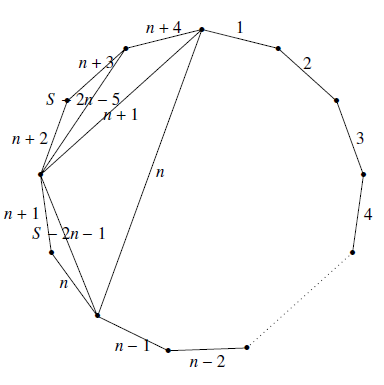先将正 $n+4$ 边形用一条对角线分割成一个凸 $n$ 边形和一个凸六边形，并将这条对角线标上 $n$．由 $n$ 满足条件，可将凸 $n$ 边形分割成三角形，使得每个三角形三边所标数的和相等，设此和为 $S$．
按图中的方式将凸六边形用三条对角线分割成四个三角形，并在三条对角线上分别标上 $S-2n-1$，$n+1$，$S-2n-5$，可验证这四个三角形三边所标数之和也等于 $S$，因此 $n+4$ 也满足条件．
于是对所有 $n\geqslant 4$ 且 $n\not\equiv 2\pmod{4}$ 都满足条件．
综上所述，满足条件的 $n$ 为 $n\geqslant 4$ 且 $n\not\equiv 2\pmod{4}$．
首先证明若 $n$ 满足条件，
则 $n\not\equiv 2\pmod{4}$．
若正整数 $n$ 满足条件，设每个三角形三边所标整数之和为 $S$，所有 $n-3$ 条对角线所标整数之和为 $m$，对所有 $n-2$ 个三角形边所标数之和求和，每条对角线都计算了两次，可得 $(n-2)S=(1+2+\ldots+n)+2m$
假设 $n\equiv 2\pmod{4}$，则 $(n-2)S$ 为偶数，而 $(1+2+\ldots+n)+2m$ 为奇数，矛盾．因此 $n\not\equiv 2\pmod{4}$．
以下证明所有 $n\geqslant 4$ 且 $n\not\equiv 2\pmod {4}$ 都满足条件．
如图分别给出了 $n=4,5,7$ 时的构造，可直接验证满足条件．
下面用归纳法证明若 $n$ 满足条件，则 $n+4$ 也满足条件．如图先将正 $n+4$ 边形用一条对角线分割成一个凸 $n$ 边形和一个凸六边形，并将这条对角线标上 $n$．由 $n$ 满足条件，可将凸 $n$ 边形分割成三角形，使得每个三角形三边所标数的和相等，设此和为 $S$．按图中的方式将凸六边形用三条对角线分割成四个三角形，并在三条对角线上分别标上 $S-2n-1$，$n+1$，$S-2n-5$，可验证这四个三角形三边所标数之和也等于 $S$，因此 $n+4$ 也满足条件．
于是对所有 $n\geqslant 4$ 且 $n\not\equiv 2\pmod{4}$ 都满足条件．
综上所述，满足条件的 $n$ 为 $n\geqslant 4$ 且 $n\not\equiv 2\pmod{4}$．
答案
解析
备注
