在锐角 $\triangle ABC$ 中，$H$ 是垂心，$O$ 是外心（$A,H,O$ 三点不共线），点 $D$ 是 $A$ 在边 $BC$ 上的射影，线段 $AO$ 的中垂线交直线 $BC$ 于点 $E$．
求证：线段 $OH$ 的中点在 $\triangle ADE$ 的外接圆上．
求证：线段 $OH$ 的中点在 $\triangle ADE$ 的外接圆上．
【难度】
【出处】
2012年中国西部数学邀请赛试题
【标注】
【答案】
略
【解析】
如图所示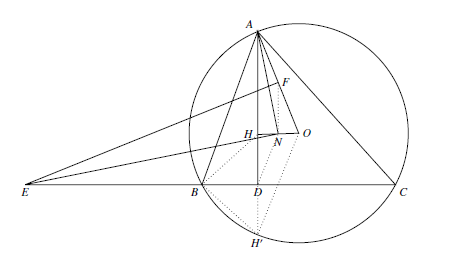
延长 $HD$ 与 $\triangle ABC$ 的外接圆交于点 $H'$，连结 $FN,DN,BH,BH',OH'$．
设 $AO$ 中点为 $F$．
因为 $H$ 是垂心，所以 $\angle CBH'=\angle CAH'=\angle CBH$，故 $D$ 是 $HH'$ 的中点．
又因为 $N$ 是 $HO$ 的中点，所以，$DN$ 是 $\triangle HOH'$ 的中位线，因此，$DN=\dfrac{1}{2}OH'$．
由 $OH'=OA$，$F$ 是 $AO$ 的中点，知 $DN=\dfrac{1}{2}OH'=\dfrac{1}{2}OA=AF$．
又 $F$ 是 $AO$ 的中点，$N$ 是 $OH$ 的中点，故 $FN\parallel AH$，所以四边形 $AFND$ 是等腰梯形，$A,F,N,D$ 四点共圆．
利用 $\angle ADE=90^{\circ}=\angle AFE$，可得 $A,F,D,E$ 四点共圆．
所以 $A,F,N,D,E$ 五点共圆．
因此，$\triangle ADE$ 的外接圆过线段 $OH$ 的中点 $N$．
延长 $HD$ 与 $\triangle ABC$ 的外接圆交于点 $H'$，连结 $FN,DN,BH,BH',OH'$．设 $AO$ 中点为 $F$．
因为 $H$ 是垂心，所以 $\angle CBH'=\angle CAH'=\angle CBH$，故 $D$ 是 $HH'$ 的中点．
又因为 $N$ 是 $HO$ 的中点，所以，$DN$ 是 $\triangle HOH'$ 的中位线，因此，$DN=\dfrac{1}{2}OH'$．
由 $OH'=OA$，$F$ 是 $AO$ 的中点，知 $DN=\dfrac{1}{2}OH'=\dfrac{1}{2}OA=AF$．
又 $F$ 是 $AO$ 的中点，$N$ 是 $OH$ 的中点，故 $FN\parallel AH$，所以四边形 $AFND$ 是等腰梯形，$A,F,N,D$ 四点共圆．
利用 $\angle ADE=90^{\circ}=\angle AFE$，可得 $A,F,D,E$ 四点共圆．
所以 $A,F,N,D,E$ 五点共圆．
因此，$\triangle ADE$ 的外接圆过线段 $OH$ 的中点 $N$．
答案
解析
备注
