如图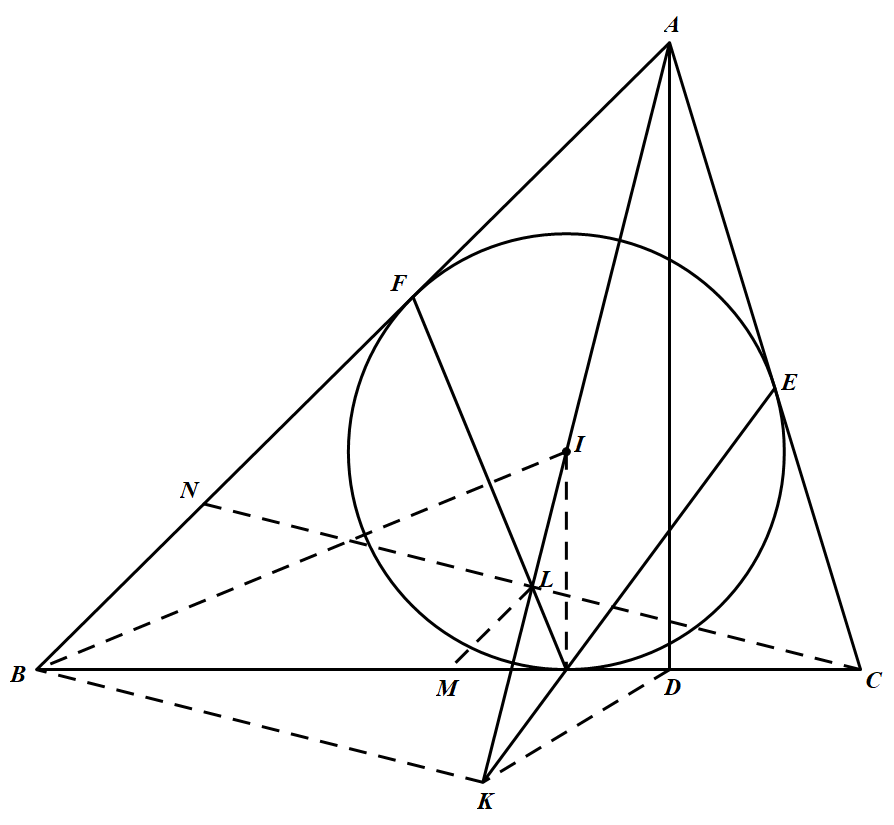
在 $\triangle ABC$ 中，$AB>AC$，内切圆 $\odot I$ 与边 $BC、CA、AB$ 分别相切于点 $D、E,F,M$ 是边 $BC$ 的中点，$AH\bot BC$ 于点 $H$．$\angle BAC$ 的平分线 $AI$ 分别与直线 $DE、DF$ 交于点 $K、L$．求证：$M、L、H、K$ 四点共圆．
在 $\triangle ABC$ 中，$AB>AC$，内切圆 $\odot I$ 与边 $BC、CA、AB$ 分别相切于点 $D、E,F,M$ 是边 $BC$ 的中点，$AH\bot BC$ 于点 $H$．$\angle BAC$ 的平分线 $AI$ 分别与直线 $DE、DF$ 交于点 $K、L$．求证：$M、L、H、K$ 四点共圆．【难度】
【出处】
2011年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
连结 $BI,DI,BK,ML,KH$，连结 $CL$ 并延长交边 $AB$ 于点 $N$．
因为 $CD、CE$ 都是 $\odot I$ 的切线，所以 $CD=CE$．因为
$\begin{aligned} \angle B I K &=\angle R A I+\angle A B I=\frac{1}{2}(\angle B A C+\angle A B C) =\frac{1}{2}\left(180^{\circ}-\angle A C B\right)=\angle E D C=\angle B D K \end{aligned}$
所以 $B、K、D、I$ 四点共圆
于是 $\angle BKI=\angle BDI= 90^\circ$，即 $BK\bot AK$，同理有 $CL\bot AL$．因为 $AL$ 是 $\angle BAC$ 的角平分线，所以 $L$ 是 $CN$ 的中点．又因为 $M$ 是 $BC$ 的中点，所以 $ML\parallel AB$．
由 $\angle BKA=\angle BHA= 90^\circ$，得 $B、K,H、A$ 四点共圆．
于是 $\angle MHK=\angle BAK=\angle MLK$，故 $M、L,H、K$ 四点共圆．
因为 $CD、CE$ 都是 $\odot I$ 的切线，所以 $CD=CE$．因为
$\begin{aligned} \angle B I K &=\angle R A I+\angle A B I=\frac{1}{2}(\angle B A C+\angle A B C) =\frac{1}{2}\left(180^{\circ}-\angle A C B\right)=\angle E D C=\angle B D K \end{aligned}$
所以 $B、K、D、I$ 四点共圆
于是 $\angle BKI=\angle BDI= 90^\circ$，即 $BK\bot AK$，同理有 $CL\bot AL$．因为 $AL$ 是 $\angle BAC$ 的角平分线，所以 $L$ 是 $CN$ 的中点．又因为 $M$ 是 $BC$ 的中点，所以 $ML\parallel AB$．
由 $\angle BKA=\angle BHA= 90^\circ$，得 $B、K,H、A$ 四点共圆．
于是 $\angle MHK=\angle BAK=\angle MLK$，故 $M、L,H、K$ 四点共圆．
答案
解析
备注
