如图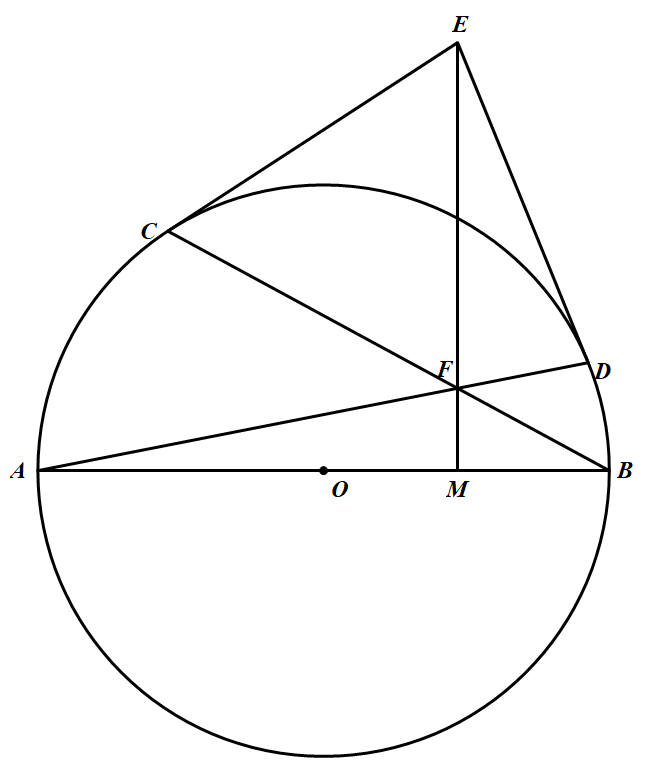
$AB$ 是 $\odot O$ 的直径，$C,D$ 是圆周上异于 $A、B$ 且在 $AB$ 同侧 的两点，分别过点 $C、D$ 作圆的切线，它们相交于点 $E$，线段 $AD$ 与 $BC$ 的交点为 $F$，直线 $EF$ 与 $AB$ 相交于点 $M$，求证：$E,C,M,D$ 四点共圆．
$AB$ 是 $\odot O$ 的直径，$C,D$ 是圆周上异于 $A、B$ 且在 $AB$ 同侧 的两点，分别过点 $C、D$ 作圆的切线，它们相交于点 $E$，线段 $AD$ 与 $BC$ 的交点为 $F$，直线 $EF$ 与 $AB$ 相交于点 $M$，求证：$E,C,M,D$ 四点共圆．【难度】
【出处】
2010年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
略
证法一
连结 $EO、CO、DO、CA$，如图所示．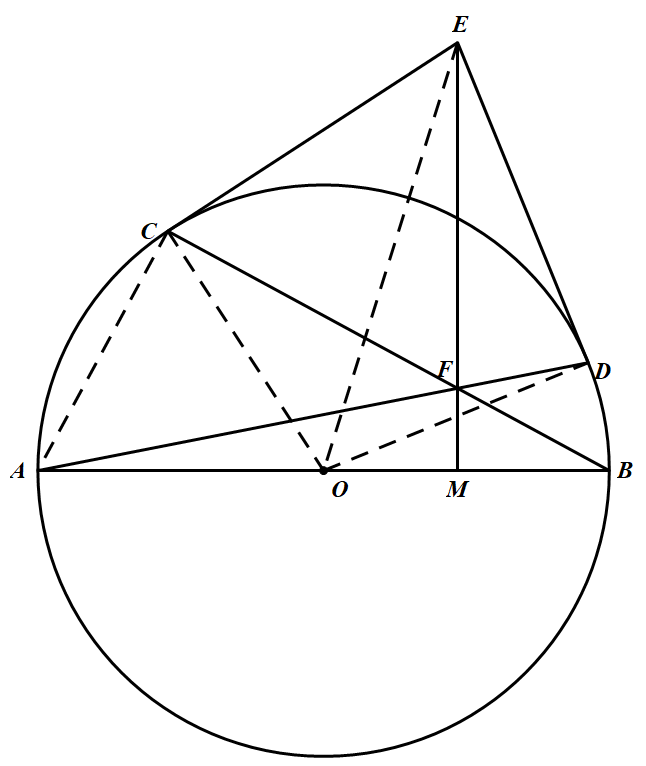
由 $\angle COE=\angle CAF$ 知，$Rt\triangle COE\sim Rt\triangle CAF$，所以 $\dfrac{C E}{C F}=\dfrac{C O}{C A}$．
又 $\angle E C F=90^{\circ}-\angle B C O=\angle O C A$，所以 $\triangle E C F \sim \triangle O C A$．故 $\angle C F E=\angle C A O$．
而 $\angle BFM=\angle CFE$，所以 $\angle F B M+\angle B F M=\angle F B M+\angle C A O=90^{\circ}$．
所以 $EM\bot AB$，因此 $O,M,D,E, C$ 五点共圆．
证法二
连结 $QC、OD、OE$，如图所示，则 $E、C、O、D$ 四点共圆．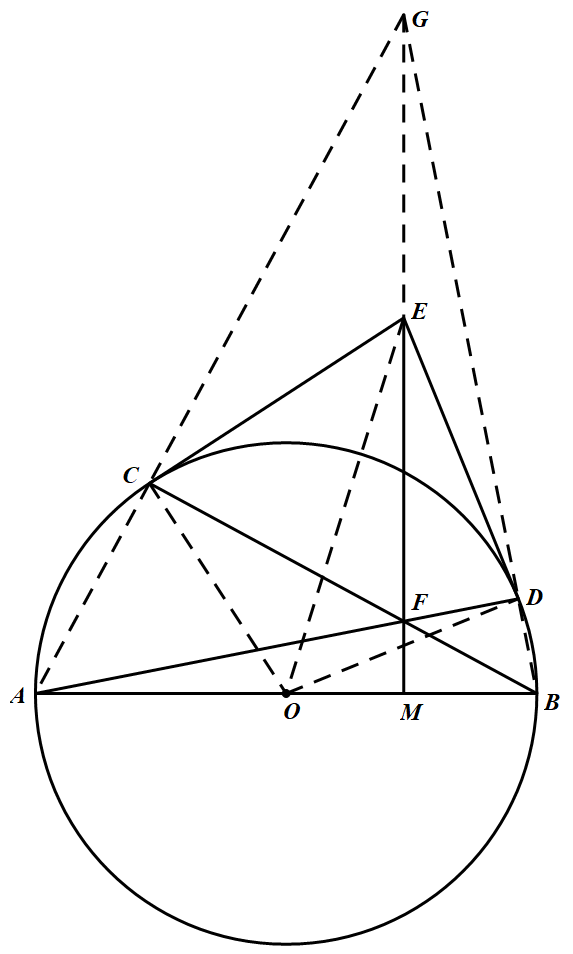
若 $O,M$ 重合，则 $E、C、M、D$ 四点共圆；
若 $O、M$ 不重合，延长 $AC、BD$ 交于点 $G$，连结 $GF$ 并延长交 $AB$ 于点 $H_1$，过 $E$ 作 $AB$ 的垂线，垂足为 $H_2$．
因为 $AD\bot BG$ 且 $BC\bot AG$，所以点 $F$ 是 $\triangle BAG$ 的垂心，于是 $GH_2\bot AB$．
由 $\angle C H_{2} D=\angle C A F+\angle D B F=180^{\circ}-2 \angle B G A$
$\begin{aligned} \angle C O D &=180^{\circ}-\angle A O C-\angle B O D \\ &=180^{\circ}-\left(180^{\circ}-2 \angle G A B\right)-\left(180^{\circ}-2 \angle G B A\right) \\ &=2(\angle G A B+\angle G B A)-180^{\circ} \\ &=180^{\circ}-2 \angle B G A \end{aligned}$
得 $\angle C H_{2} D=\angle C O D$，所以 $C、O、H_2、D$ 四点共圆．
又因为 $\angle ECO=\angle EDO=\angle EH_1O=90^\circ$，所以 $E,C,O,H_1,D$ 五点共圆．
这就说明 $H_1$ 与 $H_2$ 项合，即 $EF\bot AB$ 于 $M$．
由前面的推理可知 $E、C、M、D$ 四点共圆．
证法一
连结 $EO、CO、DO、CA$，如图所示．
由 $\angle COE=\angle CAF$ 知，$Rt\triangle COE\sim Rt\triangle CAF$，所以 $\dfrac{C E}{C F}=\dfrac{C O}{C A}$．又 $\angle E C F=90^{\circ}-\angle B C O=\angle O C A$，所以 $\triangle E C F \sim \triangle O C A$．故 $\angle C F E=\angle C A O$．
而 $\angle BFM=\angle CFE$，所以 $\angle F B M+\angle B F M=\angle F B M+\angle C A O=90^{\circ}$．
所以 $EM\bot AB$，因此 $O,M,D,E, C$ 五点共圆．
证法二
连结 $QC、OD、OE$，如图所示，则 $E、C、O、D$ 四点共圆．
若 $O,M$ 重合，则 $E、C、M、D$ 四点共圆；若 $O、M$ 不重合，延长 $AC、BD$ 交于点 $G$，连结 $GF$ 并延长交 $AB$ 于点 $H_1$，过 $E$ 作 $AB$ 的垂线，垂足为 $H_2$．
因为 $AD\bot BG$ 且 $BC\bot AG$，所以点 $F$ 是 $\triangle BAG$ 的垂心，于是 $GH_2\bot AB$．
由 $\angle C H_{2} D=\angle C A F+\angle D B F=180^{\circ}-2 \angle B G A$
$\begin{aligned} \angle C O D &=180^{\circ}-\angle A O C-\angle B O D \\ &=180^{\circ}-\left(180^{\circ}-2 \angle G A B\right)-\left(180^{\circ}-2 \angle G B A\right) \\ &=2(\angle G A B+\angle G B A)-180^{\circ} \\ &=180^{\circ}-2 \angle B G A \end{aligned}$
得 $\angle C H_{2} D=\angle C O D$，所以 $C、O、H_2、D$ 四点共圆．
又因为 $\angle ECO=\angle EDO=\angle EH_1O=90^\circ$，所以 $E,C,O,H_1,D$ 五点共圆．
这就说明 $H_1$ 与 $H_2$ 项合，即 $EF\bot AB$ 于 $M$．
由前面的推理可知 $E、C、M、D$ 四点共圆．
答案
解析
备注
