有 $n(n\geqslant 3)$ 名选手参加乒乓球比赛，每两名选手之间恰比赛一场．如果选手 $A$ 的手下败将不都是 $B$ 的手下败将，则称 $A$ 不亚于 $B$．试求所有可能的 $n$，使得存在一种比赛结果，其中每一名选手都不亚千其他任何一名选手．
【难度】
【出处】
2010年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
$n=3$ 或 $n\geqslant 5$
（1）$n = 3$ 时，可构造如图所示的比赛结果（箭头指向被打败的选手），易见此时符合要求．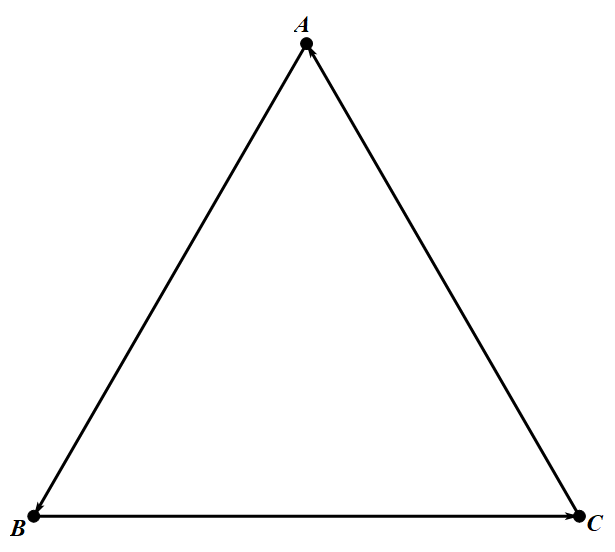
（2）$n = 4$ 时，假设存在一种比赛结果，使得每名选手都不亚于其他任何名选手，则显然不可能有某名选手战胜了其他所有选手（其他选手无法不亚于他），也不可能有某名选手输给了其他所有选手（他无法不亚于其他选手）．
若每名选手都战胜了 $1$ 或 $2$ 人，不妨设 $A$ 战胜了 $B$ 和 $D$，输给了 $C$，则 $B、D$ 都战胜了 $C$（否则就无法不亚于 $A$）．那么 $B、D$ 和之间比赛的负者（只战胜了 $C$）就一定无法不亚于胜者（战胜了 $C$ 和对方）．
所以，$n=4$ 时不存在满足要求的比赛结果．
（3）$n=6$ 时，可构造如图的比赛结果：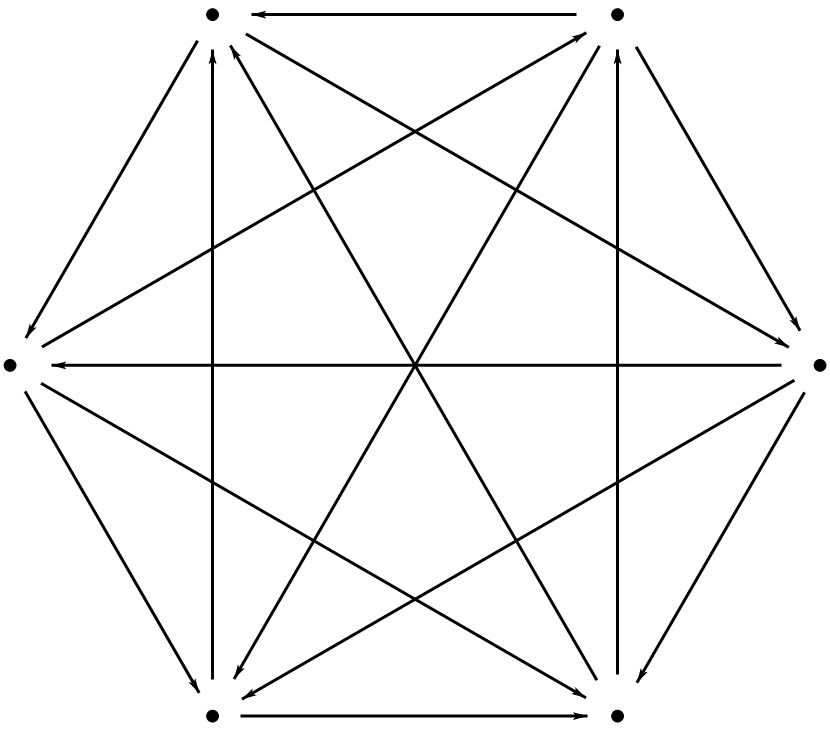
（4）若存在一种 $n$ 名选手的比赛结果，其中每一名选手不亚于其他任何一名选手，记比赛结果可用图 $G$ 来表示，则增加两名选手 $M$ 和 $N$，构造比赛结果如下图
首先 $M$ 不亚于 $N$，$N$ 也不亚于 $M$；
对于 $G$ 中的任意一名选手 $P$，由于 $P$ 的手下败将有 $M$ 而没有 $N$，$M$ 的手下败将有 $N$ 而没有 $M$，所以 $P$ 不亚于 $M$，$M$ 也不亚于 $P$；由于 $P$ 的手下败将有 $M$ 而没有 $P$，$N$ 的手下败将有 $P$ 而没有 $M$，所以 $P$ 不亚于 $N$，$N$ 也不亚于 $P$．
因此这个比赛结果符合要求．
综上所述，满足题目要求的 $n$ 的集合是 $\{n \in \mathbf{N} | n \geqslant 3, n \neq 4\}$．
（1）$n = 3$ 时，可构造如图所示的比赛结果（箭头指向被打败的选手），易见此时符合要求．
（2）$n = 4$ 时，假设存在一种比赛结果，使得每名选手都不亚于其他任何名选手，则显然不可能有某名选手战胜了其他所有选手（其他选手无法不亚于他），也不可能有某名选手输给了其他所有选手（他无法不亚于其他选手）．若每名选手都战胜了 $1$ 或 $2$ 人，不妨设 $A$ 战胜了 $B$ 和 $D$，输给了 $C$，则 $B、D$ 都战胜了 $C$（否则就无法不亚于 $A$）．那么 $B、D$ 和之间比赛的负者（只战胜了 $C$）就一定无法不亚于胜者（战胜了 $C$ 和对方）．
所以，$n=4$ 时不存在满足要求的比赛结果．
（3）$n=6$ 时，可构造如图的比赛结果：
（4）若存在一种 $n$ 名选手的比赛结果，其中每一名选手不亚于其他任何一名选手，记比赛结果可用图 $G$ 来表示，则增加两名选手 $M$ 和 $N$，构造比赛结果如下图首先 $M$ 不亚于 $N$，$N$ 也不亚于 $M$；对于 $G$ 中的任意一名选手 $P$，由于 $P$ 的手下败将有 $M$ 而没有 $N$，$M$ 的手下败将有 $N$ 而没有 $M$，所以 $P$ 不亚于 $M$，$M$ 也不亚于 $P$；由于 $P$ 的手下败将有 $M$ 而没有 $P$，$N$ 的手下败将有 $P$ 而没有 $M$，所以 $P$ 不亚于 $N$，$N$ 也不亚于 $P$．
因此这个比赛结果符合要求．
综上所述，满足题目要求的 $n$ 的集合是 $\{n \in \mathbf{N} | n \geqslant 3, n \neq 4\}$．
答案
解析
备注
