设 $H$ 为锐角 $\triangle ABC$ 的垂心，$D$ 为边 $BC$ 的中点．过点 $H$ 的直线分别交边 $AB、AC$ 于点 $F、E$，使得 $AE=AF$．射线 $DH$ 与 $\triangle ABC$ 的外接圆交于点 $P$．
求证：$P,A,E,F$ 四点共圆．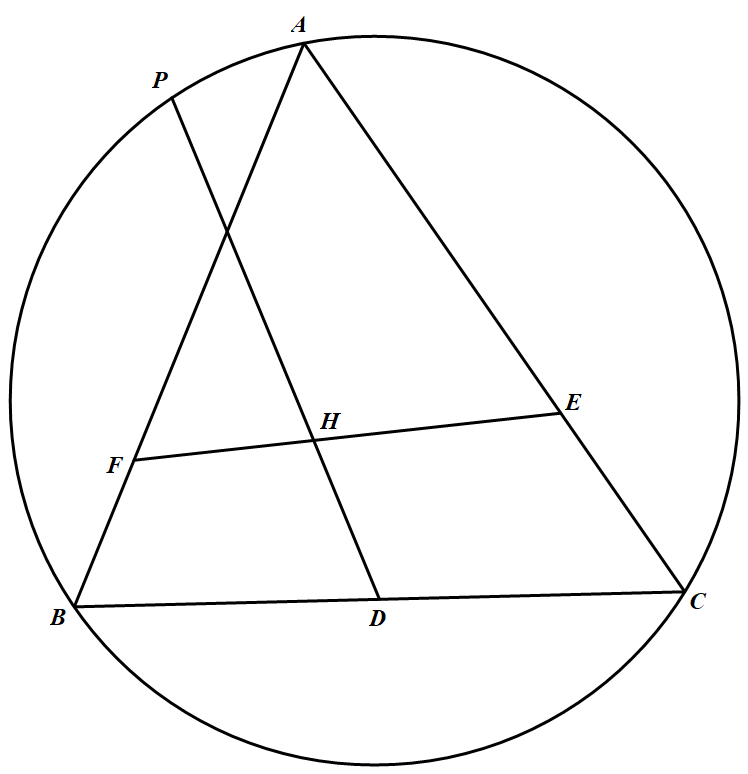
求证：$P,A,E,F$ 四点共圆．
【难度】
【出处】
2009年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
延长 $HD$ 至点 $M$ 使 $HD=DM$，连结 $BM,CM,BH,CH$．因为 $D$ 为边 $BC$ 的中点，所以四边形 $BHCM$ 是平行四边形，故 $\angle B M C=\angle B H C=180^{\circ}-\angle B A C$，
即 $\angle B M C+\angle B A C=180^{\circ}$，所以点 $M$ 在 $\triangle ABC$ 的外接圆上．
连结 $PB、PC、PE、PF$，因为 $AE=AF$，所以 $\angle B F H=\angle C E H$ ①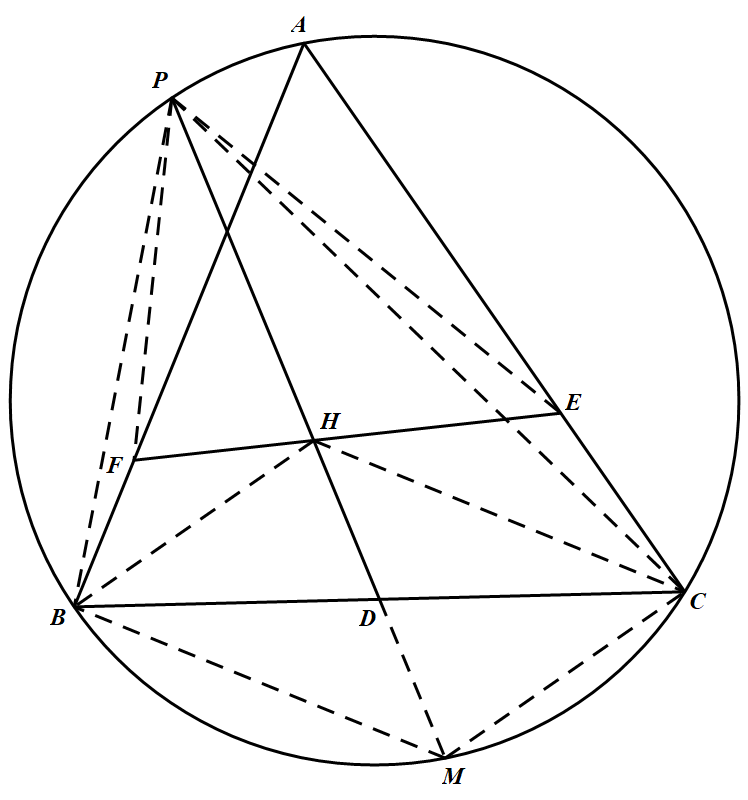
因为 $H$ 是 $\triangle ABC$ 的垂心，所以 $\angle H B F=90^{\circ}-\angle B A C=\angle H C E$ ②
结合 ①，② 知，$\triangle B F H \sim \triangle C E H$，所以 $\dfrac{B F}{B H}=\dfrac{C E}{C H}$．
又由 $BHCM$ 是平行四边形知 $BH=CM,CH=BM$，所以 $\dfrac{B F}{C M}=\dfrac{C E}{B M}$ ③
又因为 $D$ 为 $BC$ 的中点，所以 $S_{\triangle P B M}=S_{\triangle F C M}$，所以 $\dfrac{1}{2} B P \cdot B M \cdot \sin \angle M B P=\dfrac{1}{2} C P \cdot C M \cdot \sin \angle M C P$，
由 $\angle M B P+\angle M C P=180^{\circ}$，可得 $B P \cdot B M=C P \cdot C M$ ④
结合 ③，④ 知，$\dfrac{BF}{BP}=\dfrac{CE}{CP}$．
因为 $\angle P B F=\angle P C E$，所以 $\triangle P B F \subset \triangle P C E$，故 $\angle P F B=\angle P E C$，于是 $\angle P F A=\angle P E A$，故 $P,A,E,F$ 四点共圆．
即 $\angle B M C+\angle B A C=180^{\circ}$，所以点 $M$ 在 $\triangle ABC$ 的外接圆上．
连结 $PB、PC、PE、PF$，因为 $AE=AF$，所以 $\angle B F H=\angle C E H$ ①
因为 $H$ 是 $\triangle ABC$ 的垂心，所以 $\angle H B F=90^{\circ}-\angle B A C=\angle H C E$ ②结合 ①，② 知，$\triangle B F H \sim \triangle C E H$，所以 $\dfrac{B F}{B H}=\dfrac{C E}{C H}$．
又由 $BHCM$ 是平行四边形知 $BH=CM,CH=BM$，所以 $\dfrac{B F}{C M}=\dfrac{C E}{B M}$ ③
又因为 $D$ 为 $BC$ 的中点，所以 $S_{\triangle P B M}=S_{\triangle F C M}$，所以 $\dfrac{1}{2} B P \cdot B M \cdot \sin \angle M B P=\dfrac{1}{2} C P \cdot C M \cdot \sin \angle M C P$，
由 $\angle M B P+\angle M C P=180^{\circ}$，可得 $B P \cdot B M=C P \cdot C M$ ④
结合 ③，④ 知，$\dfrac{BF}{BP}=\dfrac{CE}{CP}$．
因为 $\angle P B F=\angle P C E$，所以 $\triangle P B F \subset \triangle P C E$，故 $\angle P F B=\angle P E C$，于是 $\angle P F A=\angle P E A$，故 $P,A,E,F$ 四点共圆．
答案
解析
备注
